10.2. Фундаментальна система розв’язків
З розглянутих вище властивостей випливає, що з будь-яких двох частинних розв’язків системи лінійних однорідних рівнянь можна скласти безліч розв’язків даної системи як різні лінійні комбінації цих розв’язків.
В зв’язку з цим виникає питання, чи не можна всі розв’язки системи однорідних лінійних рівнянь подати як лінійні комбінації кількох певних розв’язків.
Виявляється, що можна знайти так звану фундаментальну систему розв’язків характерну тим, що кожний розв’язок однорідної системи є якоюсь лінійною комбінацією розв’язків фундаментальної системи.
Зрозуміло, що фундаментальна система розв’язків має бути лінійно незалежною, бо у протилежному випадку один з розв’язків сам був би лінійною комбінацією інших розв’язків даної системи і тому його можна було б відкинути.
Означення. Фундаментальною системою розв’язків системи однорідних лінійних рівнянь називається така лінійно незалежна сукупність її розв’язків, що всякий розв’язок даної системи є якоюсь лінійною комбінацією розв’язків з цієї сукупності.
Доведено, що для довільної однорідної системи (10.1) з рангом r n існує фундаментальна система розв’язків. Число розв’язків цієї системи дорівнює n - r.
Для знаходження фундаментальної системи отримують спочатку загальний розв’язок однорідної системи рівнянь, а потім надають вільним невідомим числові значення рядків детермінанта (n - r)-го порядку діагонального виду.
Одержані таким чином частинні розв’язки однорідної системи складають фундаментальну систему розв’язків.
Якщо
(n-r)
=
,
то фундаментальна система розв’язків
називається нормованою.
Вправи. Знайти нормовану фундаментальну систему розв’язків для систем:
1)
Відповідь:
.
2)
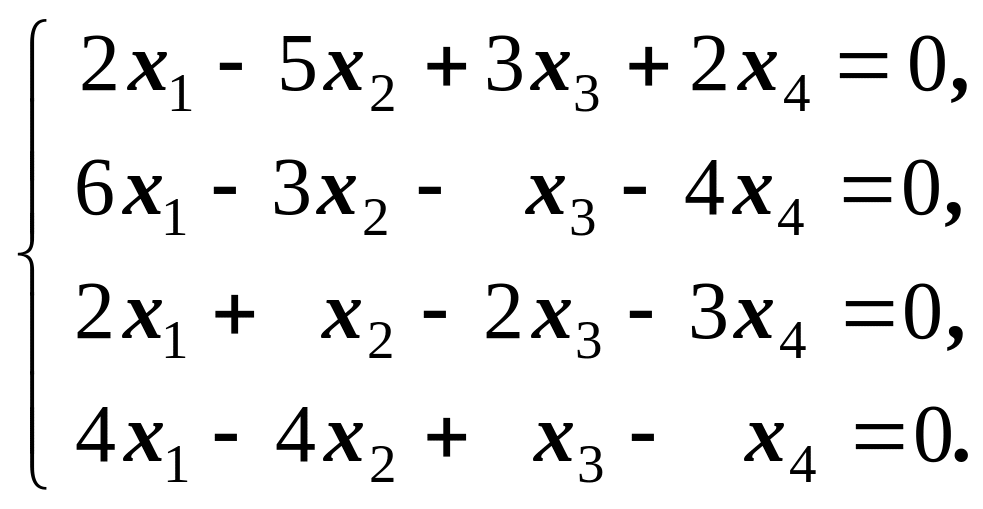
Відповідь:
,
.
11. Метод Гаусса
Метод Гаусса — це метод послідовного виключення невідомих. Запишемо розширену матрицю
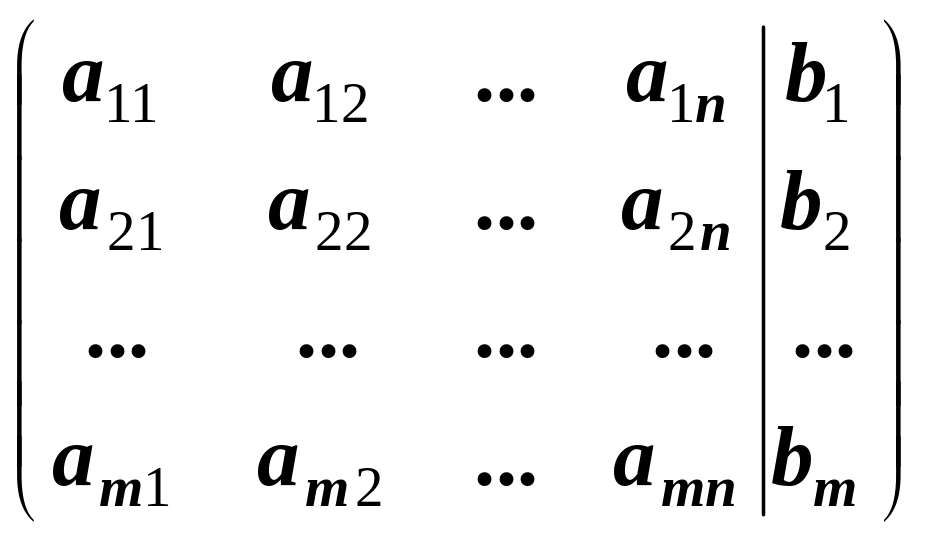
системи m лінійних рівнянь з n невідомими і для встановлення її рангу будемо виконувати елементарні перетворення лише над рядками матриці. Ці елементарні перетворення відповідають елементарним перетворенням над рівняннями системи, які не змінюють її розв’язків (множення рівняння на дійсне число відмінне від нуля, складання рівнянь та переставлення їх місцями).
Тоді, після встановлення сумісності системи для знаходження її розв’язків необхідно записати систему рiвнянь, що відповідає останній перетвореній матриці системи. Ця система має трикутний вигляд і містить r рівнянь.
Знайдемо із останнього (r-го) рівняння цієї системи базисну невідому xr і підставимо її в попереднє ( (r-1) - шe) рівняння. Знайдемо xr-1 і т.д., поки не дійдемо до першого рівняння, з якого знаходимо x1.
Вправи. Розв’язати системи методом Гаусса:
1)
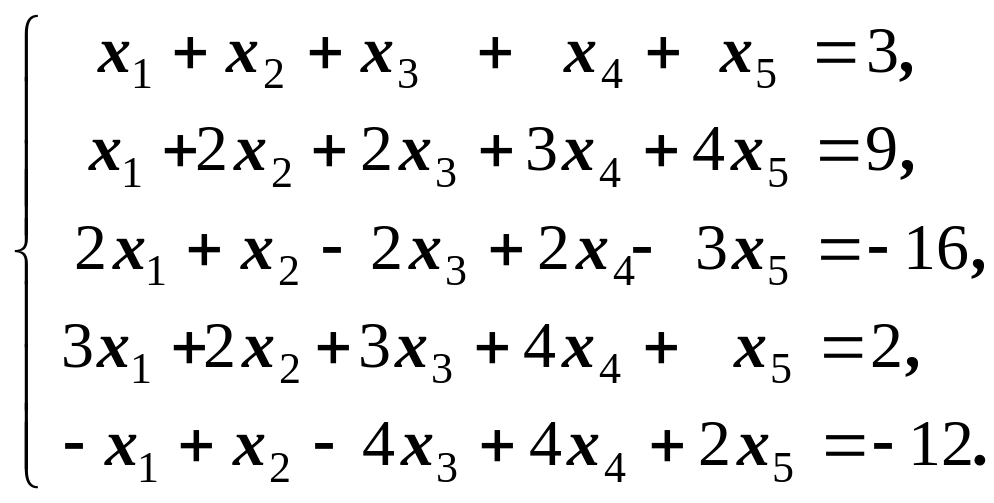
Відповідь: (1, -1, 2, -2, 3)Т.
2)
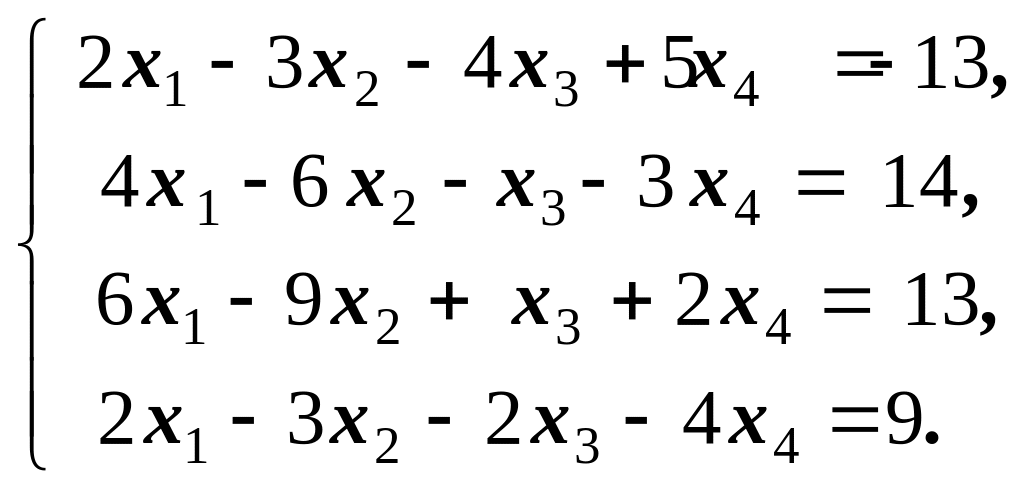
Відповідь:
.
3)
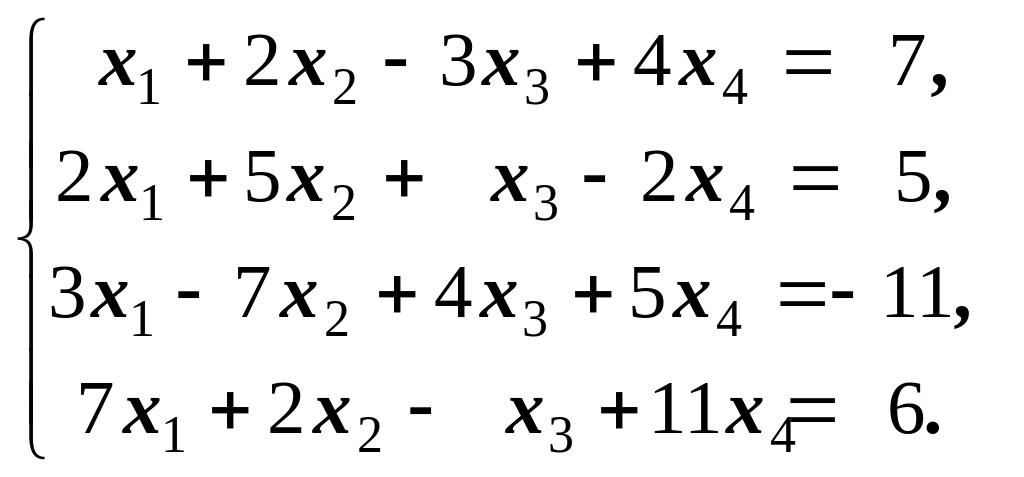
Відповідь: Система несумісна.
12. Зв’язок між розв’язками неоднорідної та зведеної систем
Нехай маємо неоднорідну систему лінійних рівнянь
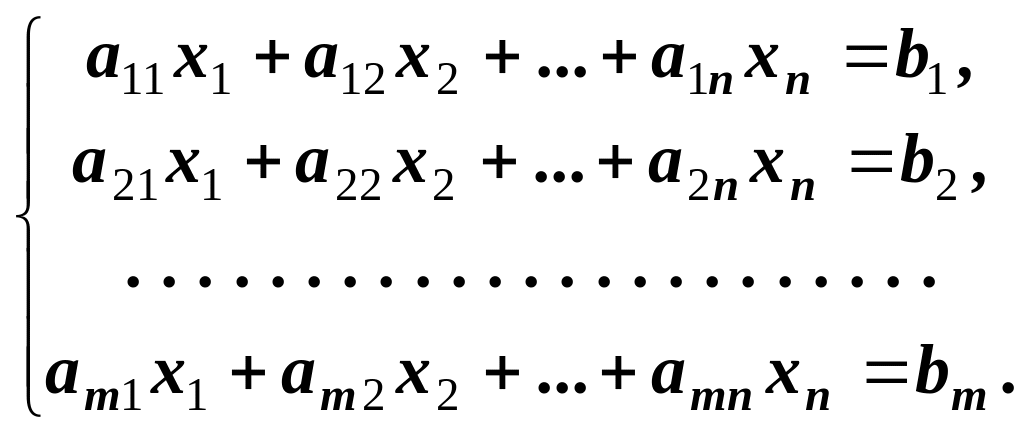(12.1)
Цій системі відповідає однорідна система
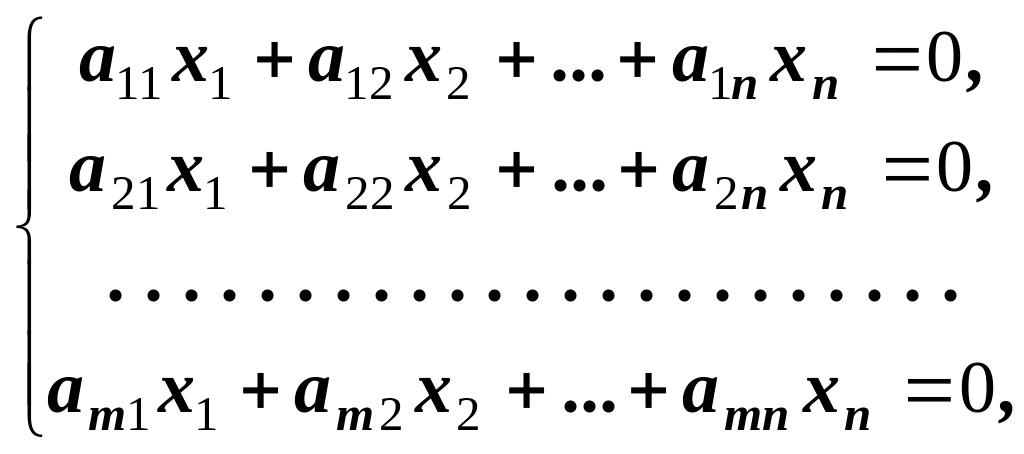(12.2)
яку називають зведеною відносно системи (12.1).
Для систем (12.1) та (12.2) мають місце дві леми, які приймаємо без доведення.
Лема 1
Якщо — частинний розв’язок неоднорідної системи (12.1), а — частинний розв’язок зведеної системи (12.2), то + — розв’язок системи (12.1).
Лема 2
Якщо 1 та 2 — довільні частинні розв’язки системи (12.1), то 1 - 2 — розв’язок зведеної системи (12.2).
Ці леми використовують при доведенні такої теореми.
Загальний розв’язок неоднорідної системи дорівнює сумі якогось частинного розв’язку цієї системи і загального розв’язку зведеної системи.
З використанням
фундаментальної системи загальний
розв’язок зведеної системи , ранг якої
дорівнює
,
може бути записаний у вигляді
,
де
— довільні сталі,
,
,
,
…,
.
Тоді загальний розв’язок неоднорідної системи лінійних рівнянь має вигляд
,
або
.
Проілюструємо справедливість теореми на прикладі.
Знайти загальний розв’язок неоднорідної системи
Розв’яжемо систему методом Гаусса
=
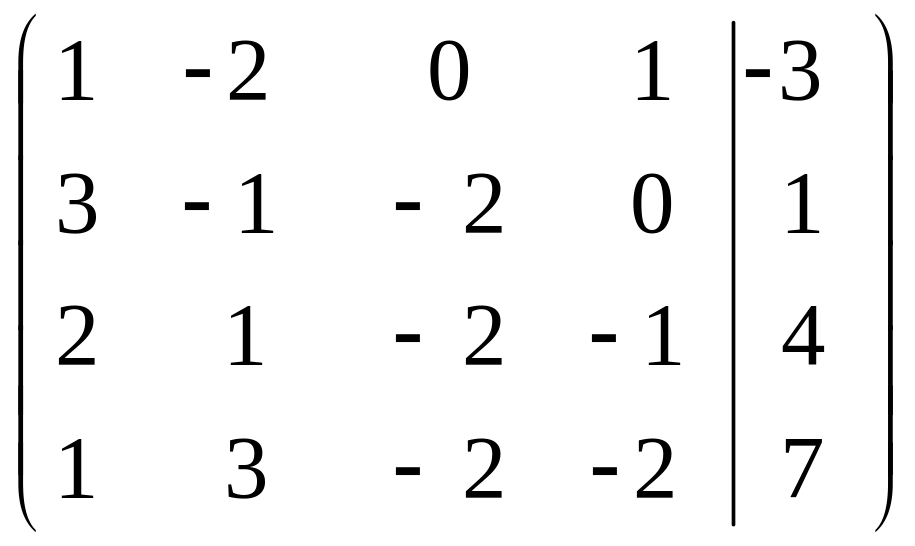
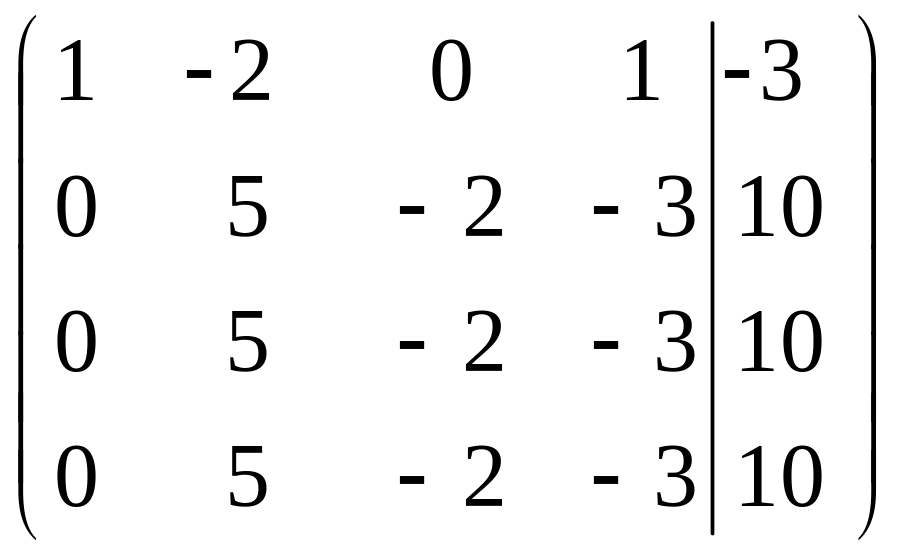
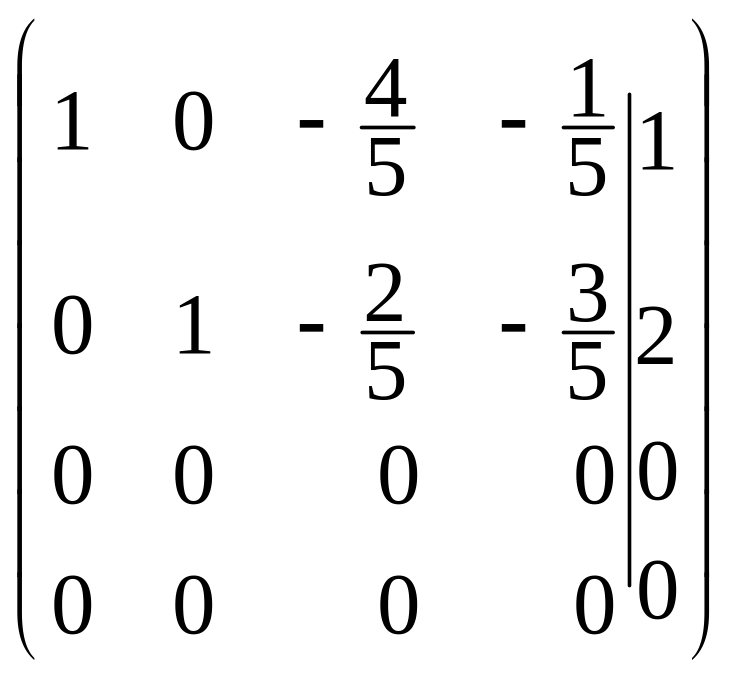
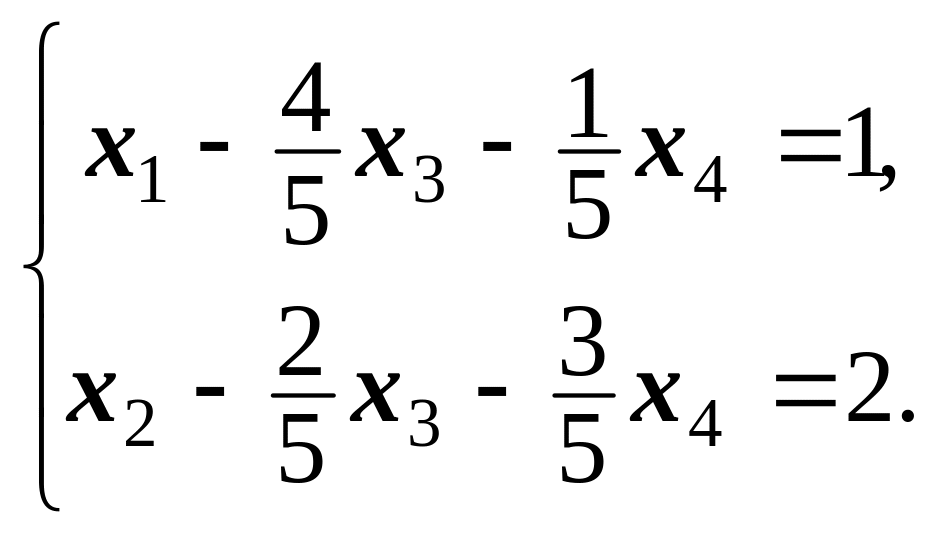
Вважаючи
x1,
x2
базисними невідомими, а x3
та x4
вільними
,
отримаємо загальний розв’язок
Х(С1,С2)
=
=
=
+
,
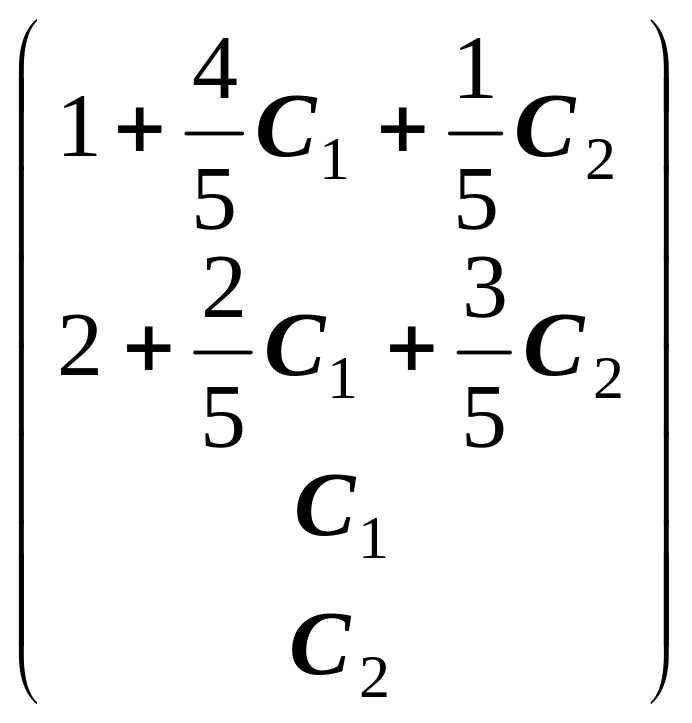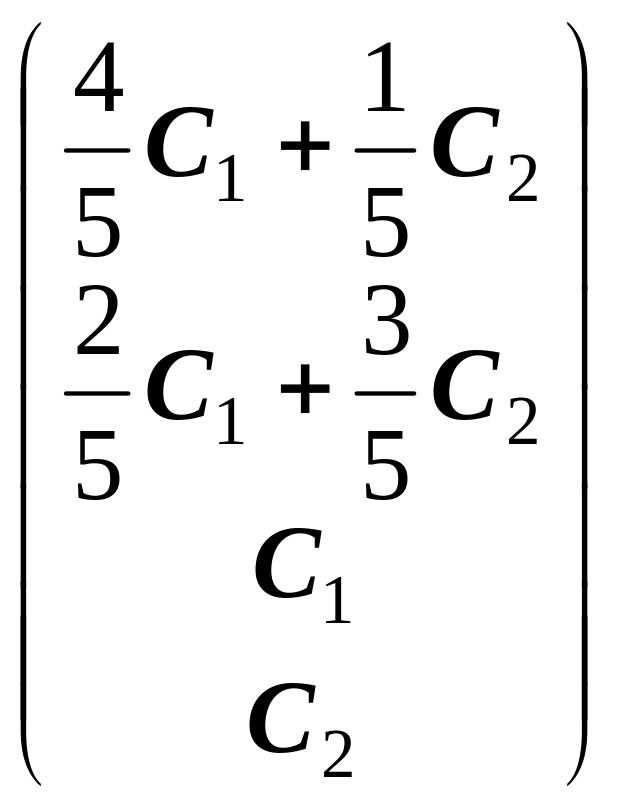де = Хч — частинний розв’язок неоднорідної системи,
=
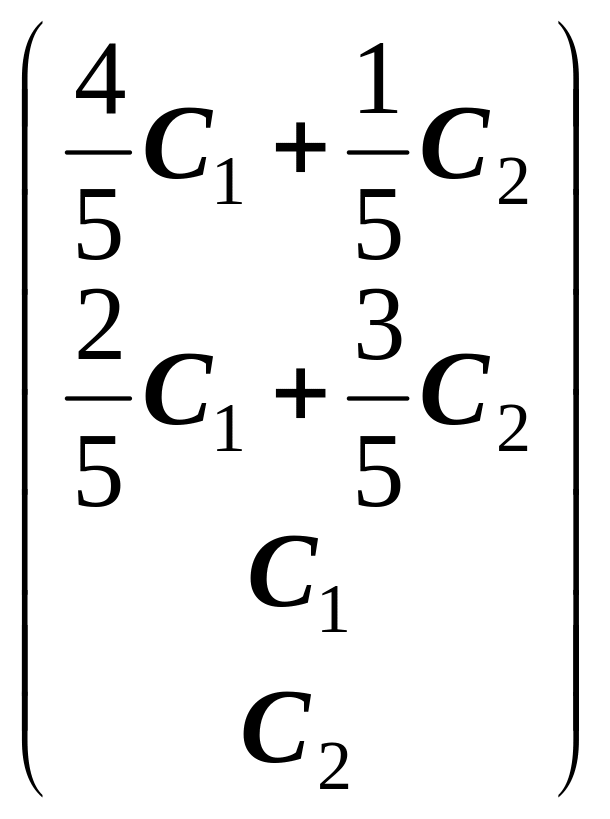Х0(С1,С2)
— загальний розв’язок зведеної системи.
Оскільки Х0(С1,С2) = С1 Е1 + С2 Е2,
де Е1
=
Х0(1,0)
=
,
Е2
=
Х0(0,1)
=
є
фундаментальна система розв’язків, то
Х(С1,С2) = + С1 + С2 .
Вправи. Знайти загальний розв’язок неоднорідної системи
та записати його використовуючи фундаментальну систему розв’язків:
1)
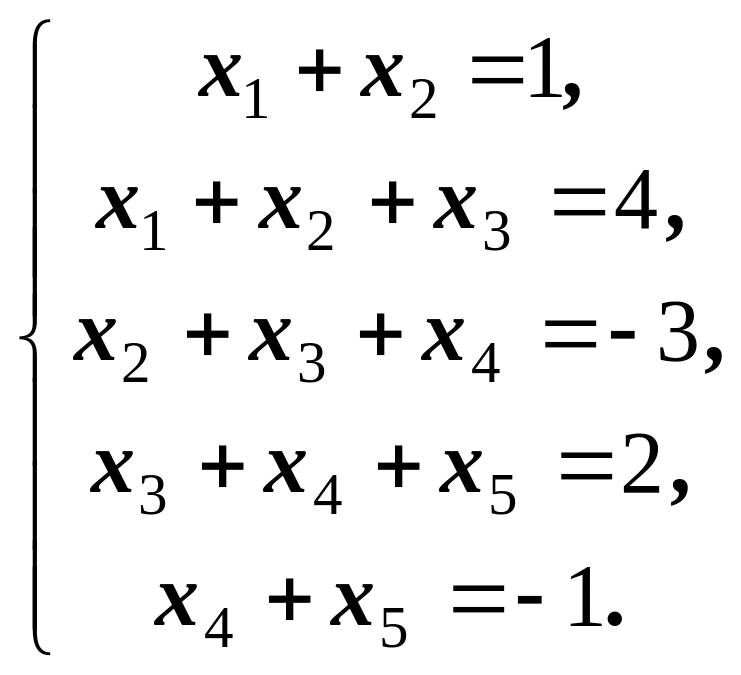
Відповідь:
,
,
2)
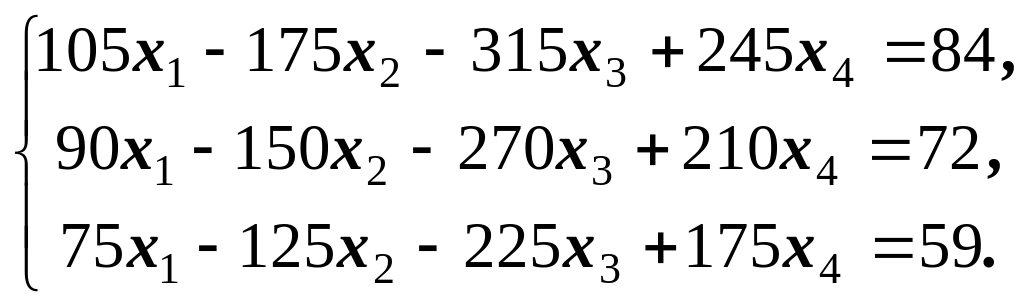
Відповідь: система несумісна.
3)
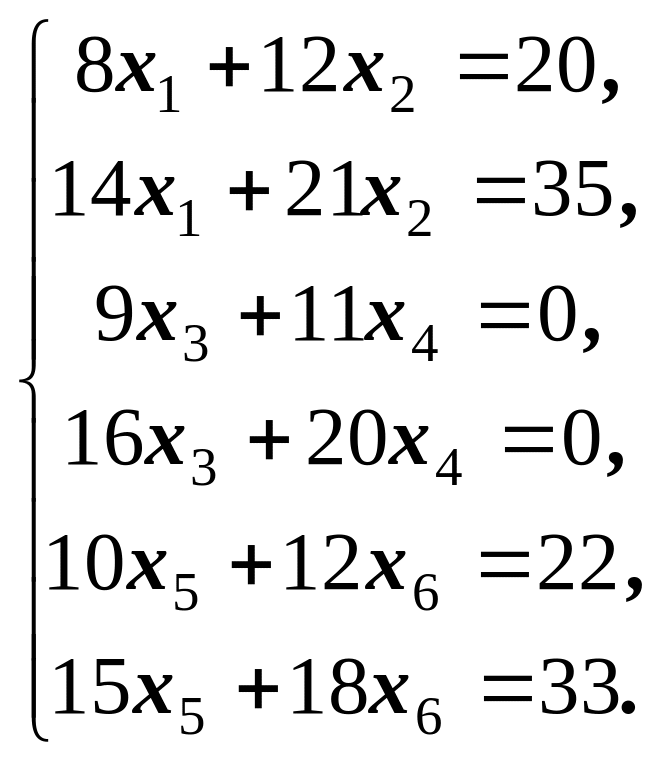
Відповідь:
,
,
,
.