Е лементи лінійної алгебри

6. Розв’язування матричних рівнянь

за допомогою оберненої матриці

1. Розв’язування квадратних

матричних рівнянь

Розглянемо матричні рівняння або , де матриці і — квадратні однакового порядку , крім того матриця має обернену матрицю. Тоді ці рівняння можна розв’язати шляхом множення зліва (справа)обох частин рівняння на матрицю . Отримаємо

Вправи. Розв’язати системи:

1) . Відповідь: .

2) . Відповідь: .

3) . Відповідь: .

6.2. Розв’язування квадратних лінійних систем

Розглянемо матричне рівняння AX = B, що відповідає квадратній лінійній системі рівнянь

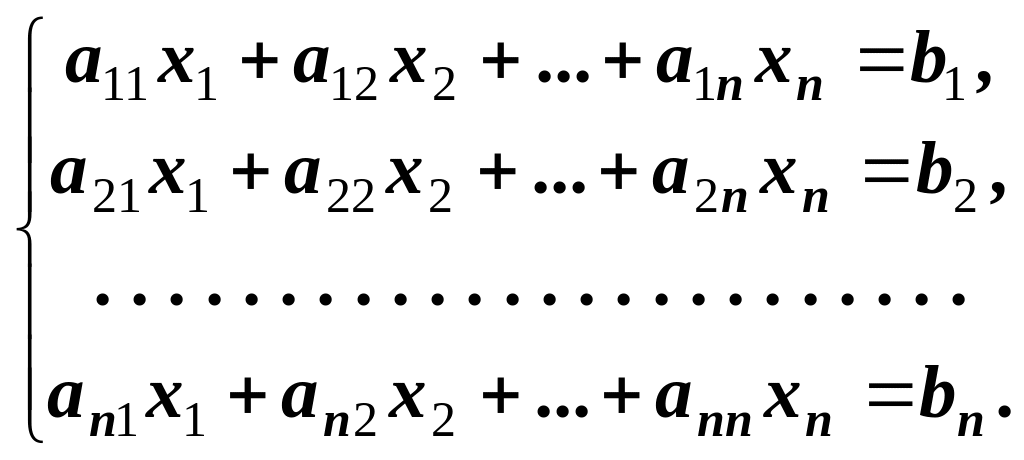(6.1)

А = — матриця системи, detA  0,

X = — матриця невідомих,

B = — матриця вільних членів.

Для знаходження матриці Х використаємо формулу

Вправи. Розв’язати системи:

1) 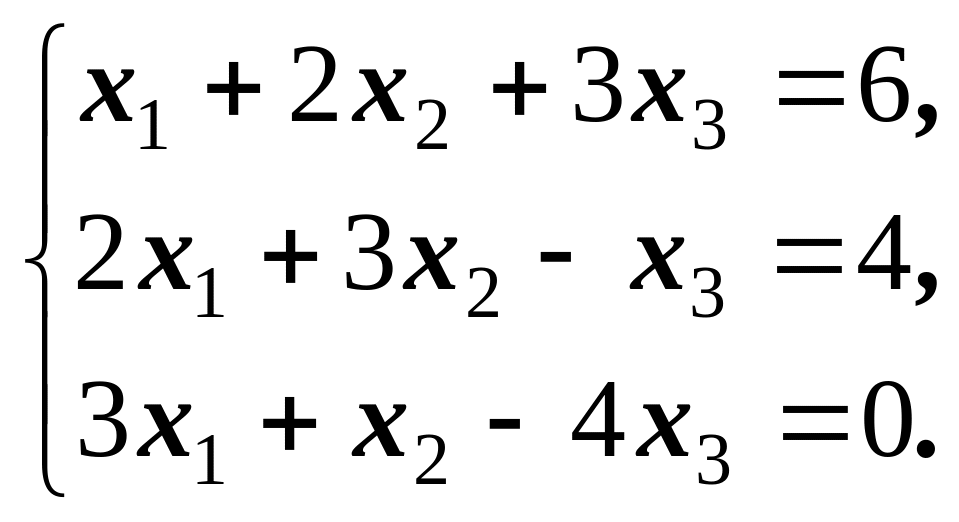Відповідь: Х =

2) 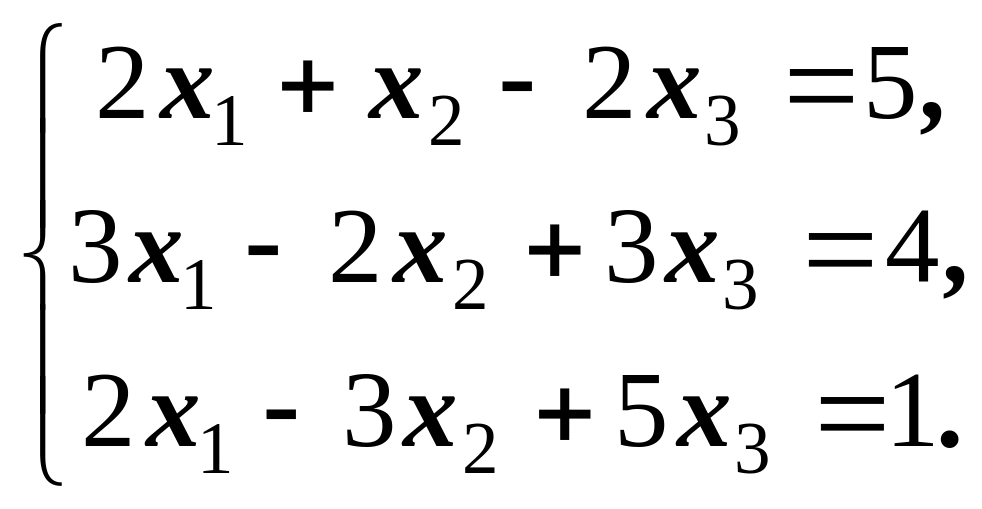Відповідь: Х =

3) 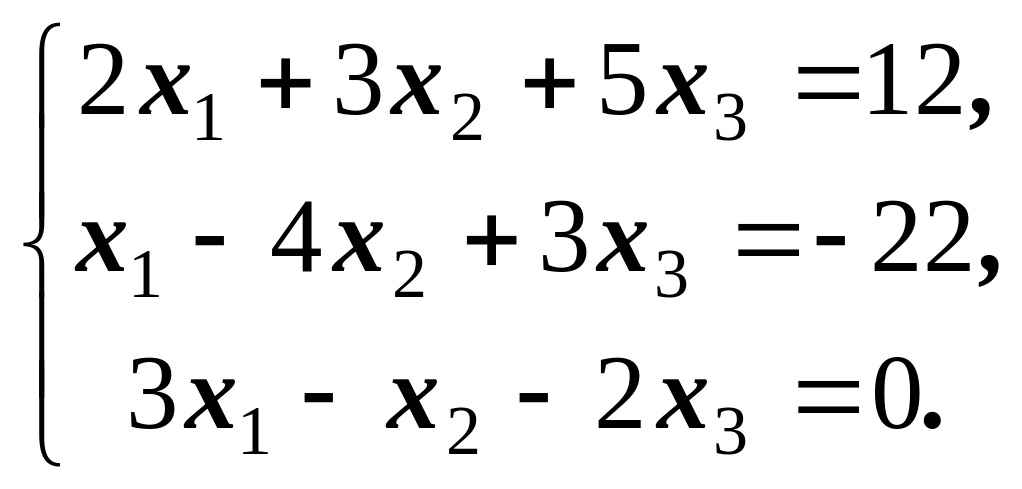Відповідь: Х = .

7. Поняття рангу та базисного мінору матриці. Знаходження рангу матриці

Розглянемо матрицю A_mn . Розбиваючи її горизонтальними та вертикальними прямими на матриці (блоки, клітини) меншого порядку, одержимо так звану блочну матрицю, елементами якої будуть матриці.

Наприклад,

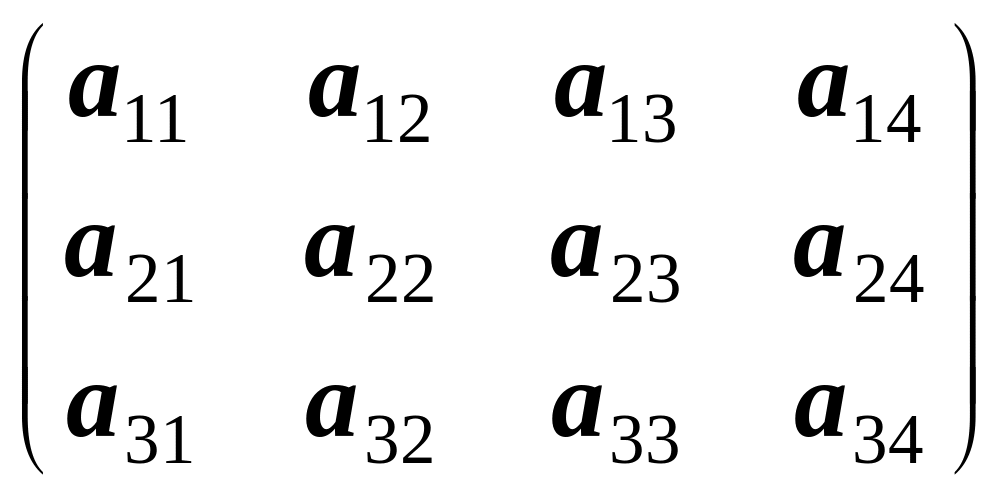
А _3x4 =  M_2x3 = ,

де М_2х3 — блочна ( клітинна) матриця.

Матрицю A_mn можна розбити на блоки таким чином, що її елементами будуть тільки рядки або тільки стовпці первісної матриці

A_mn = = ,

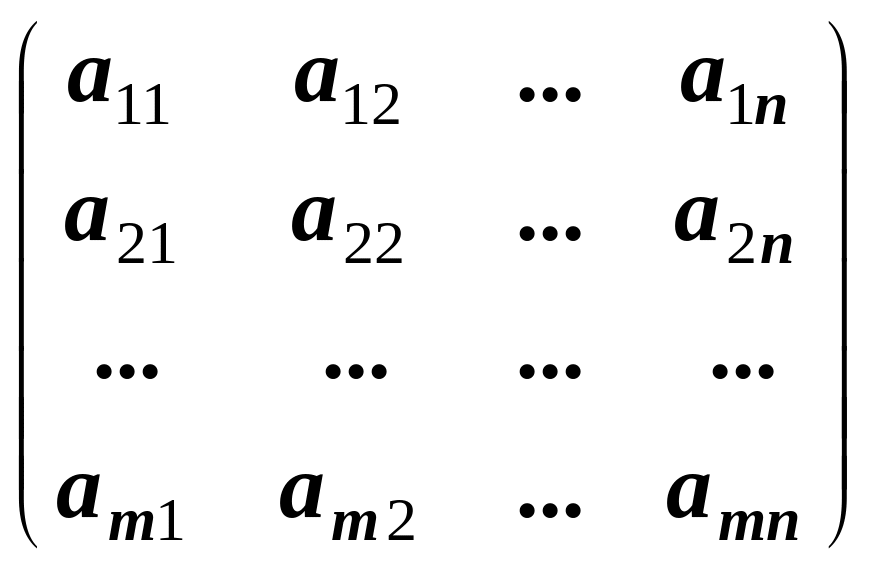де , , ... ,

А_mn = = ,

де , , ... , .

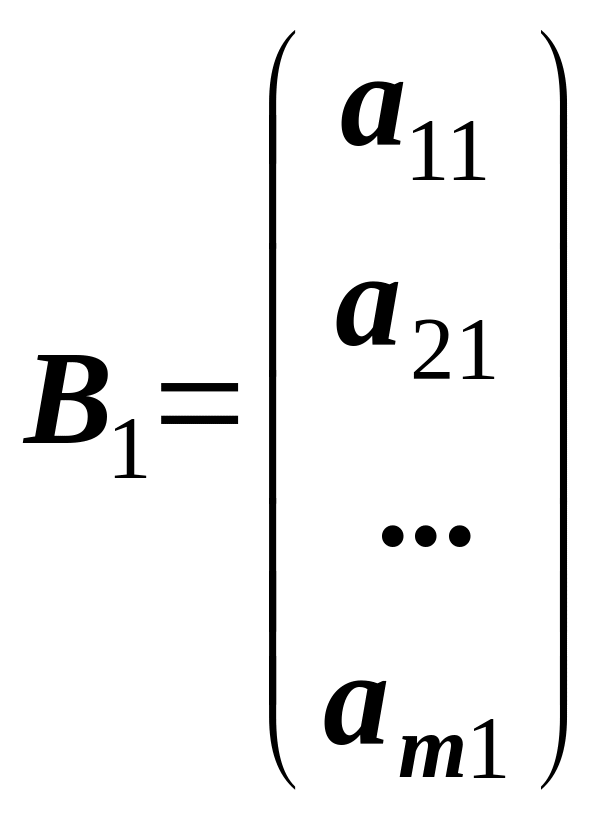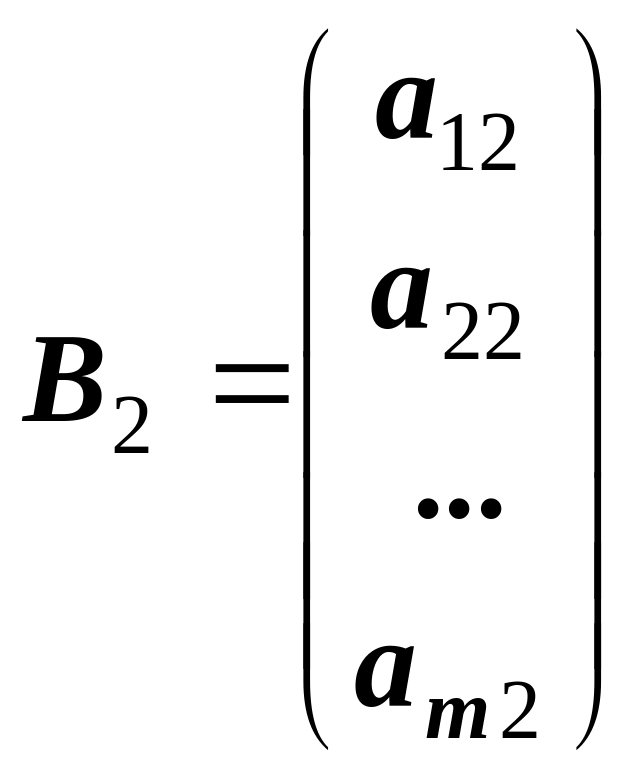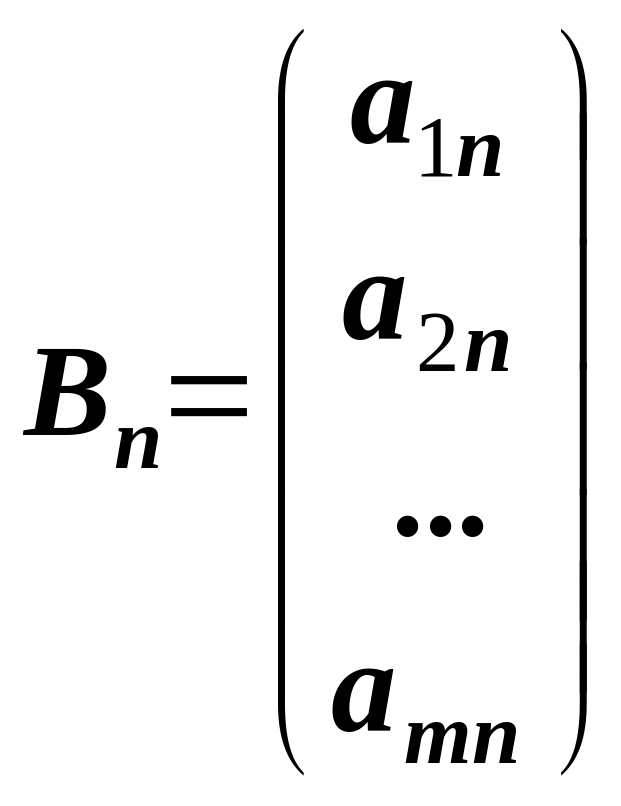Розглянемо нульову лінійну комбінацію складену із стовпців матриці A_mn.

k₁В₁+k₂В₂+...+k_nВ_n = 0 (7.1)

Або коротко: .

Якщо рівність (7.1) справджується за умови, що всі коефіцієнти k_i = 0, то стовпці матриці A_mn є лінійно незалежні; якщо ж деякі із коефіцієнтів рівності (7.1) не дорівнюють нулю, то стовпці матриці А_mn є лінійно залежні.

У випадку лінійної залежності будь-який із стовпців може бути поданий як лінійна комбінація інших стовпців.

Виділимо в матриці А_mn які-небудь s рядків і s стовпців (1  s  min(m,n)). Тоді сукупність елементів, які знаходяться на перетині виділених рядків і стовпців, утворює квадратну матрицю s-го порядку, детермінант якої називається мінором s-го порядку даної матриці.

Наприклад, із матриці

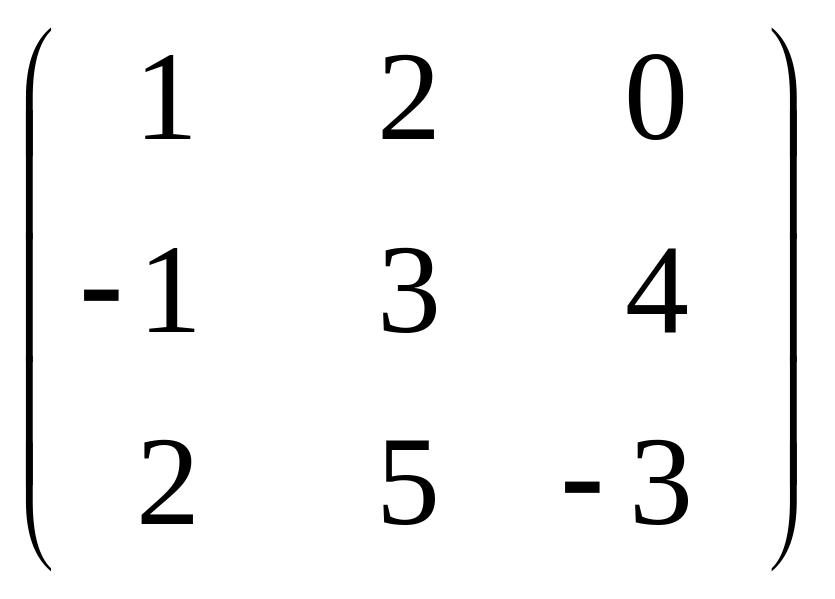
можна скласти 9 мінорів першого порядку, 9 мінорів другого порядку, 1 мінор третього порядку:

М₁⁽¹⁾ = |1|, M₂⁽¹⁾ = |2|, M₃⁽¹⁾ = |0| і т.д.

М₁⁽²⁾ = , M₂⁽²⁾ = , M₃⁽²⁾ = і т. д.

М⁽³⁾ = .

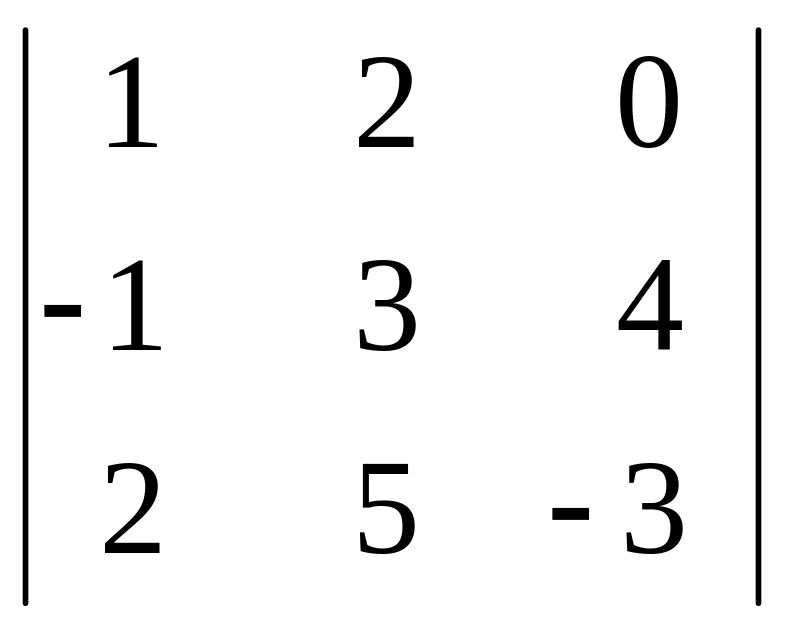Означення. Рангом матриці А називають найвищий порядок відмінного від нуля мінора цієї матриці і позначають RgA або rangA.

Отже, ранг матриці дорівнює r, якщо існує мінор цієї матриці r-го порядку, що відмінний від нуля, а всі мінори

(r + 1)-го порядку дорівнюють нулю або не існують.

Вправи. Знайти ранг матриць:

1) А = (1 5 7).

Відповідь: RgA = 1.

2) B = .

Відповідь: RgB = 1.

3) C = .

Відповідь: RgC = 2.

4) D = .

Відповідь: RgD = 2.

5) E = .

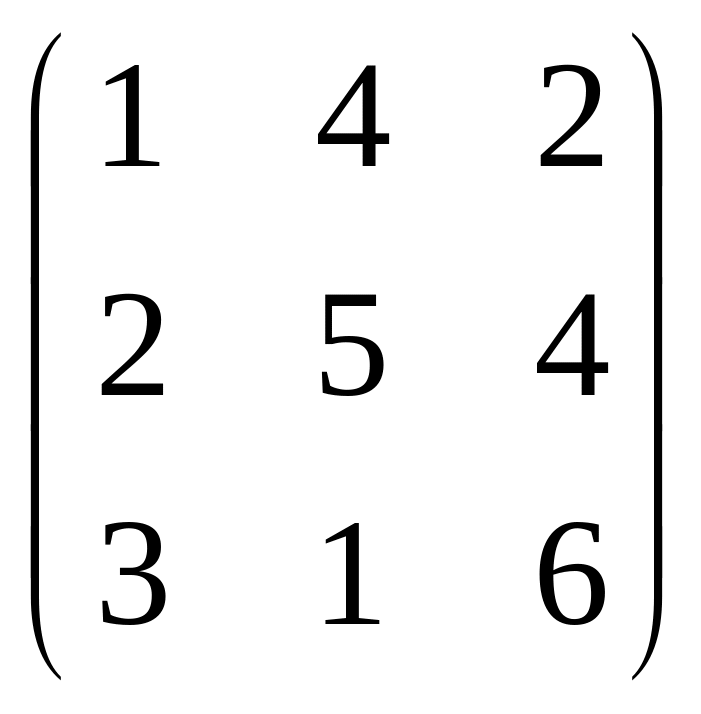Відповідь: RgE = 2.

6) K = .

Відповідь: RgK = 3.

7) M = .

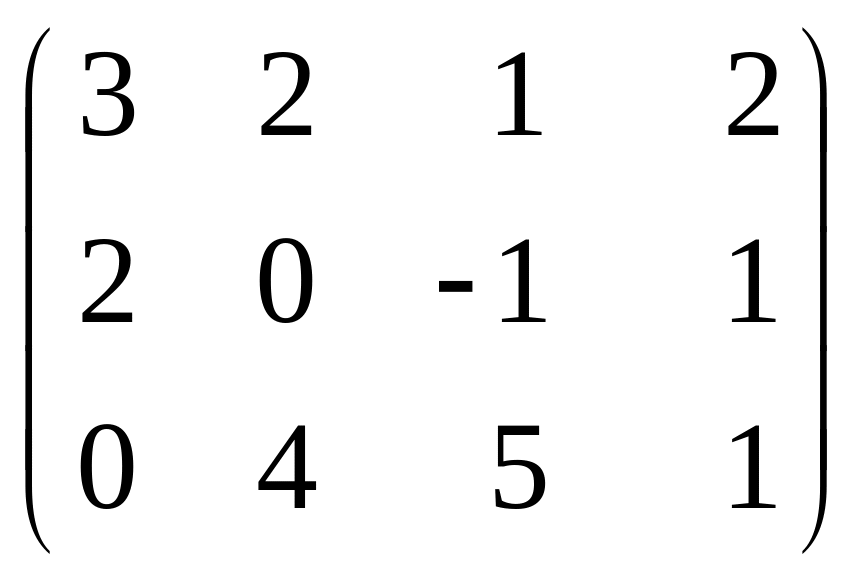Відповідь: RgM = 2.

Зауважимо, що безпосередньо (згідно з означенням) знайти ранг матриці, як правило, важко, оскільки у деяких випадках треба обчислювати дуже багато мінорів, що утворені з даної матриці. Тому надалі ми будемо використовувати так званий метод обвідних мінорів, що випливає з теореми про базисний мінор.

Означення. Базисним мінором матриці називають відмінний від нуля її мінор, порядок якого дорівнює рангу матриці. Звичайно, такий мінор, взагалі кажучи, не єдиний.

Рядки і стовпці, на перетині яких знаходяться елементи базисного мінору, називають базисними.

Наведемо без доведення так звану теорему про базисний мінор.

Усі рядки (стовпці) базисного мінора матриці A лінійно незалежні, а будь-який інший рядок (стовпець) матриці А є лінійна комбінація рядків (стовпців) базисного мінора.

Із цієї теореми випливає метод обвідних мінорів. Суть його полягає у тому, що при знаходженні рангу матриці переходять від мінорів меншого порядку до мінорів вищого порядку; причому, якщо уже знайдено мінор r-го порядку, що відмінний від нуля, то обчислюють лише ті мінори (r+1)-го порядку, що обводять (тобто містять у собі) цей мінор. Якщо всі вони дорівнюють нулю, то ранг матриці дорівнює r.

Метод обвідних мінорів особливо зручно застосовувати по відношенню до трапецоїдної матриці (зокрема трикутної), так як у цьому випадку дуже легко обчислити необхідні нам мінори.

Наприклад, для трикутної матрицi

А =

очевидно, що ранг дорiвнює 4, а для трапецоїдної матриці

В =

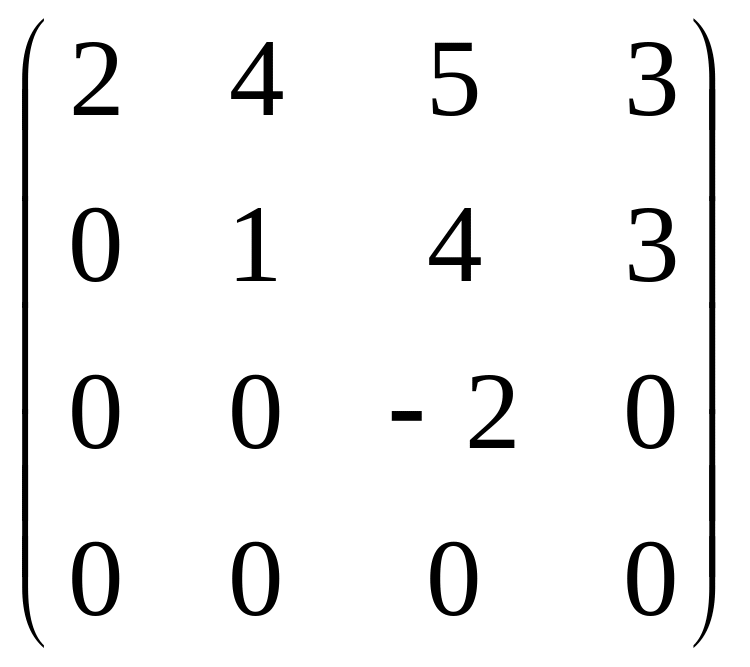
ранг дорівнює 3, тобто числу ненульових рядків цієї матриці.

В тому випадку, коли матриця не є трапецоїдною, то її можна звести до трапецоїдного виду, застосовуючи елементарні перетворення, які не порушують рангу матриці.

До таких елементарних перетворень відносять такі операції:

а) множення рядка (або стовпця) на довільне дійсне число, яке відмінне від нуля;

б) переставлення (транспозиція) двох рядків (або стовпців);

в) додавання до якогось рядка (або стовпця) іншого рядка (або стовпця), помноженого на довільне число.

Слід зауважити, що зводячи матрицю до трапецоїдного виду треба домогтися того, щоб по “головній діагоналі” були розташовані спочатку елементи, що не дорівнюють нулю (тобто при ), а потім нульові ( при , якщо вони є). Тоді ранг матриці дорівнює числу не рівних нулю елементів “головної діагоналі” (числу ненульових рядків матриці).

Вправи. Визначити ранг матриць методом окантованих мінорів:

1) А = .

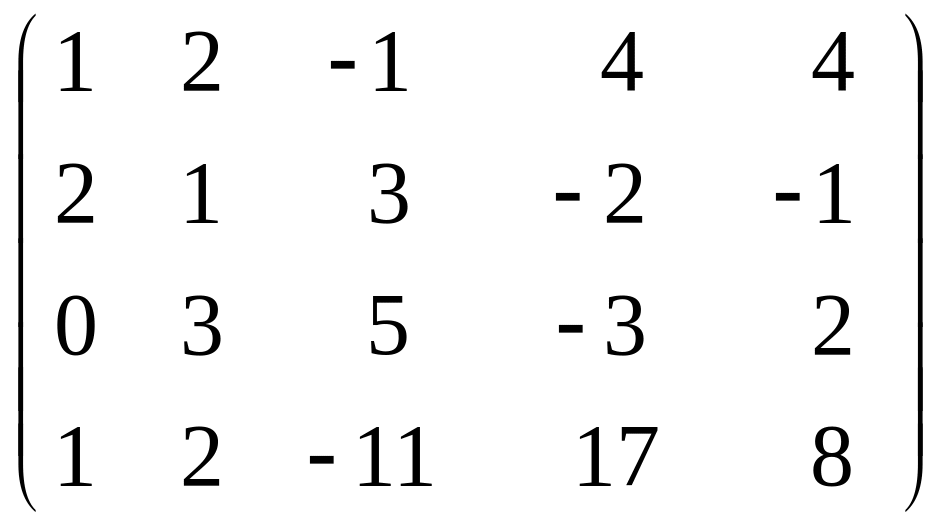Відповідь: RgA = 4.

2) B = .

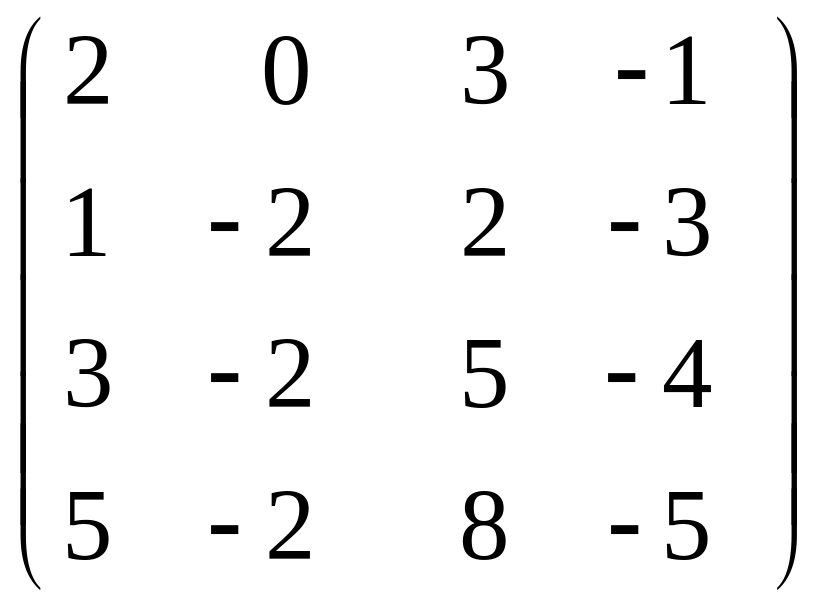Вiдповiдь: RgB = 2.

3) C = .

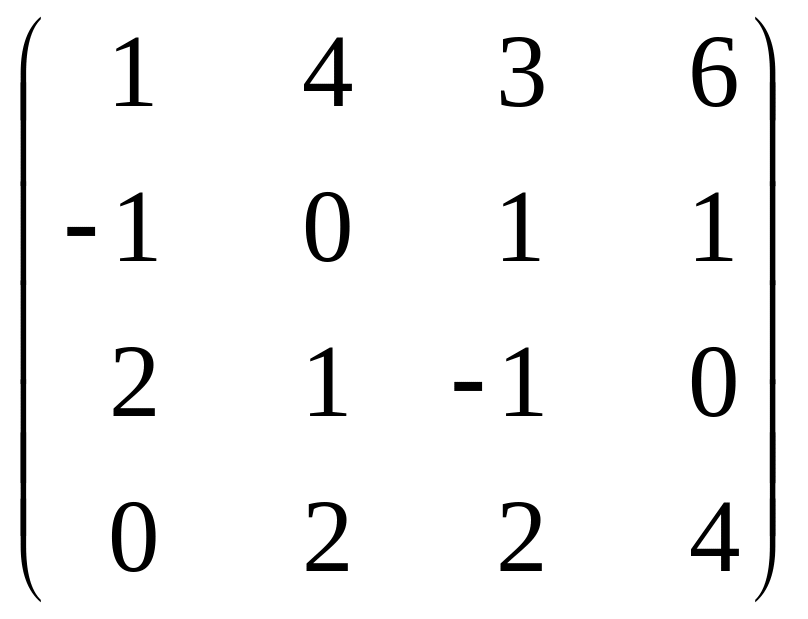Вiдповiдь: RgC = 3.