Тема 2. Химическая термодинамика и термохимия

Основные понятия термодинамики

Предмет термодинамики. Окружающий нас мир представляет собой различные формы движущейся материи. Мерой движения материи является энергия, проявляющаяся в различных ее видах. Взаимные превращения различных видов энергии, связанные с переходом энергии в форме теплоты и работы, изучает термодинамика. Применение термодинамики к химическим процессам составляет предмет химической термодинамики, которая изучает превращение различных видов энергии при химических реакциях, процессах растворения, испарения, кристаллизации и др.

Зная законы химической термодинамики, можно предсказать, возможна ли данная реакция при данных условиях или нет, и при каких условиях она станет возможной, каков будет выход продуктов реакции, т. е. какова степень превращения исходных веществ в конечные, каким тепловым эффектом она будет сопровождаться. Энергетическая сторона химических процессов имеет важное значение, так как выделяющееся при этом тепло позволяет использовать реакции горения газообразного, жидкого и твердого топлива в качестве источника тепловой энергии. Кроме того, данные об энергетических эффектах реакций используются для определения прочности межатомных и межмолекулярных связей, для выяснения строения и реакционной способности химических соединений и т. д.

Термодинамические системы. Системой называется тело или группа тел, выделенных фактически или мысленно из окружающей среды. Системой может быть газ в баллоне, стакан чая, кристалл сахара и т. п. Особенность систем, рассматриваемых в термодинамике, заключается в том, что они состоит из большого числа частиц — молекул или атомов. К отдельным молекулам, атомам или элементарным частицам законы термодинамики не применимы.

Фазой называется совокупность всех однородных частей системы, обладающих одинаковыми свойствами и отделенных от остальных частей системы поверхностью раздела. Например, жидкая вода представляет собой одну фазу, а система «жидкая вода — лед» содержит две фазы, которые хотя и обладают одинаковым химическим составом, но различаются по свойствам (по внутреннему строению, плотности и др.) и имеют поверхность раздела.

Все термодинамические системы можно разделить на две большие группы — гомогенные и гетерогенные. Гомогенными (однофазными) называются системы, состоящие только из одной фазы, например воздух — смесь газов, раствор поваренной соли и сахара в воде. Здесь между составными частями систем отсутствует поверхность раздела.

Системы, содержащие две или большее число фаз, называются гетерогенными (разнофазными, неоднородными). Например, лед, вода и находящийся над ними пар образуют гетерогенную систему, состоящую из трех фаз: твердой (лед), жидкой (вода) и газообразной (водяной пар); нерастворившиеся кристаллы поваренной соли в воде образуют гетерогенную систему из двух фаз и т. д. В гетерогенной системе составные ее части— фазы — разделены поверхностью раздела.

Термодинамическая система может быть открытой, закрытой и изолированной. Система, которая может обмениваться веществом с окружающей средой, называется открытой, например сосуд с кипящей водой. Для закрытой системы невозможен обмен веществом с окружающей средой, например газ, находящийся в баллоне. Пели, наконец, невозможен обмен ни веществом; ни энергией, такая система называется изолированной. Примером может служить запаянная ампула, полностью полированная от внешней среды.

Параметры и процессы. Физические величины, позволяющие определить состояние системы, называются параметрами состояния. В химии чаще используются следующие параметры: объем, давление, температура и концентрация. Параметры состояния, поддающиеся непосредственному изменению, принято считать основными. К ним относят температуру Т, давление р, молярный объем V, концентрацию С. Другие параметры, зависящие от основных, являются функциями основных пара­метров и называются функциями состояния.

Совокупность параметров определяет состояние системы. Математическое выражение, показывающее взаимозависимость основных параметров данной системы, называется уравнением состояния. Примером может служить уравнение состояния идеального газа: pV=RT.

Энергия, теплота, работа. Важнейшими взаимосвязанными понятиями в термодинамике являются энергия, теплота и работа. Энергия — это мера способности тела совершать работу. Из различных форм энергии для характеристики процессов особенно важное значение имеет внутренняя энергия системы. Любая система, независимо от того, в каком состоянии она находится, всегда обладает определенным запасом энергии. Внутренняя энергия системы представляет собой ее полную энергию, которая складывается из энергии движения молекул, атомов, ядер и электронов в молекулах и атомах, внутриядерной энергии, энергии межмолекулярного взаимодействия и т. п.

Внутренняя энергия системы зависит от природы составляющих ее веществ, их массы и внешних условий. Абсолютное значение внутренней энергии в какой-либо системе измерить невозможно, однако опытным путем удается определить изменение внутренней энергии системы при переходе ее из одного состояния в другое. Изменение внутренней энергии U системы при любом процессе не зависит от пути этого процесса, а зависит лишь от начального и конечного состояния системы. Следовательно, внутренняя энергия является функцией состояния системы. В отличие от внутренней энергии теплота и работа не являются функциями состояния, так как они представляют собой разные формы передачи энергии. Поэтому теплота и работа могут быть отнесены только к процессу, а не к состоянию. Работа А, совершаемая системой, обусловлена взаимодействием между системой и внешней средой, в результате чего преодолеваются внешние силы, нарушившие равновесие в системе. Например, газ, расширяясь и цилиндре с поршнем, может сжимать пружину и таким образом передавать ей часть энергии. Следовательно, работа является макрофизической формой передачи энергии от системы к системе.

Другой формой передачи энергии является теплота Q, в этом случае энергия непосредственно передается молекулами одного тела молекулам другого при их контакте. Такой обмен происходит между телами, имеющими различную температуру.

Поскольку теплота и работа в количественном отношении являются мерой передаваемой энергии, то количество их измеряется в тех же единицах, что и энергия, — в джоулях (Дж).

Часто говорят, что теплота (или работа) подводится к системе или отводится от нее. Однако это не совсем строгое выражение, и, употребляя его, не следует забывать, что подводится и отводится не теплота или работа, а энергия в форме теплоты или работы. Если система обменивается энергией с окружающей средой, то в какой бы форме это ни происходило, количество энергии, полученное системой, обозначается знаком. «+», а количество энергии, отданное системой, знаком «—». Например, если система получила энергию в форме теплоты, то это можно обозначить + Q, а если система отдала теплоту, то — Q.

Работа расширения А идеального газа описывается уравнением

А = , ( 1.1 )

Р – давление, V₁ – начальный объем, V₂ –конечныйобъем.

Изучая зависимость объема V данной массы газа от давления р, Бойль (Англия) и Мариотт (Франция) независимо друг от друга открыли следую­щий закон: объем данной массы газа при постоянной температуре обратно пропорционален давлению, под ко­торым газ находится,

что можно записать уравнением

  p₁V₁ = p₂V₂ = k                                ( 1.2 )

 

где k — постоянная величина.

Таким образом, из закона Бойля — Мариотта вытека­ет, что произведение объема газа на давление при данной температуре есть величина постоянная.

Зависимость объема газа от температуры. Как и все тела, газы при нагревании расширяются, причем весьма заметно даже при незначительном нагревании. Исследуя тепловое расширение газов, француз­ский ученый Гей-Люссак установил, что для данной мас­сы идеального газа объем при постоянном давлении прямо пропорционален абсолютной температуре. Этот закон получил название закона Гей-Люссака:

V=kT                      (1.3 )

где V — объем газа; Т — абсолютная температура, К (К —градусы в шкале Кельвина, 1К=273 + °С); k — константа.

Нормальными на­зывают условия, когда температура равна 0° С (273 К) и давление составляет 1 атм, или 760 мм рт. ст. (101 325 Па). При этих условиях, как следует из закона Авогадро, 1 моль газа занимает объем 22,4 л (а 1 кмоль — 22,4 м³). Число молекул, содержащихся в 1 моле, назы­вается постоянной Авогадро:  N_A = 6,02ּ10²³ (в СИ 6,02ּ10²⁶)

Зависимость давления газа от темпера­туры. Нагревая газ в закрытом сосуде, по манометру можно заметить, что давление газа увеличивается. За­висимость давления газа от температуры при постоянном объеме выражается следующим законом: для данной массы идеального газа давление при постоянном объеме прямо пропорционально абсолютной температуре:

 p = кТ,                                  (1.4 )

 где р — давление    газа;   Т — абсолютная   температура; k — константа.

Этот закон по имени французского ученого, открывшего его, называется законом Шарля.

Объединенное уравнение состояния идеального газа. Мы рассмотрели состояния газов, когда одна из трех величин, характеризующих эти состоя­ния (объем, давление или температура), не меняется. Например, если не меняется температура, то давление и объем газа связаны друг с другом законом Бойля — Мариотта. При постоянном давлении объем газа меняется с изменением температуры по закону Гей-Люссака и, наконец, при постоянном объеме давление газа меняется с изменением температуры по закону Шарля.

Однако нередки процессы, когда одновременно меня­ются все три параметра, характеризующих состояние га­за. Соотношение, которое одновременно связывает меж­ду собой значения давления, объема и температуры (р, V и T), называется уравнением состояния идеальных газов:

PV = RT (1.5)

Уравнение ( ) называется уравнением Клапейро­на— Менделеева.

Уравнением Клапейрона — Менделеева пользуются при расчетах различных параметров, характеризующих газ или его состояние: давления р, объема V, темпе­ратуры T, массы т или молекулярной массы М.

Чтобы пользоваться уравнением Клапейрона — Мен­делеева, необходимо найти значение универсальной га­зовой постоянной R.        

В Международной системе единиц (СИ) R = 8,313 10³ Дж/(град-моль).

В зависимости от условий уравнение (1.1) принимает различный вид:

1. Р – const, изобарное расширение:

A = p (V₂ – V₁) (1.6)

Т – const, изотермическое расширение:

А = , находим p из уравнения; в

p = и подставляем ( 1.1 )

А = RT ln (1.7)

При Т – const P₁V₁ = RT = P₂V₂ (закон Бойля-Мариотта), т.е.

= , подставим в (1.7):

А = RT ln (1.8)

Количество теплоты Q, необходимое для нагрева тела, зависит от

условий:

1. V – const,

Q_V = C_V (T₂ −T₁ ) (1.9)

где С_V – изохорная теплоемкость (количество теплоты, которое надо затратить для нагревания одного моля вещества на один градус при постоянном объеме).

2. P – const:

Q_P = C_P (T₂ −T₁ ) (1.10)

где C_p – изобарная теплоемкость (количество теплоты, которое необходимо затратить на нагревание одного моля вещества на один градус при постоянном давлении).

Для одноатомного газа

С = и С_P - C_V = R (1.11)

Для молекул, состощих из двух атомов С_V = ;

Для молекул, состощих из трех атомов С_V = 3R.

Если при нагревании (или охлаждении) происходит фазовый переход

(замерзание, плавление, испарение, конденсация), то это необходимо учитывать,

Q_{ф.п =} λ, (1.12)

где λ – теплота фазового перехода;

Q_ф.п – теплота фазового перехода.

Основные положения термодинамики даются в форме трех ее законов (начал). Первый закон (первое начало) термодинамики вытекает из закона сохранения энергии. Согласно этому закону энергия не исчезает бесследно и не возникает из ничего, а лишь переходит из одной формы в другую в строго эквивалентных количествах.

Первое начало термодинамики устанавливает соотношение между теплотой Q и работой А при изменении общего запаса энергии системы. Изменение внутренней энергии системы может происходить при поглощении или выделении теплоты или при совершении работы системой или над системой. При поглощении системой некоторого количества теплоты внутренняя энергия системы увеличивается, если же в результате этого изменяется объем системы, то совершается работа по изменению объема.

Имеется несколько формулировок первого закона термодинамики, однако все они отражают неуничтожимость и эквивалентность энергии при переходе различных видов ее друг в друга:

1. В изолированной системе сумма всех видов энергии есть величина постоянная.

2. Невозможно создать вечный двигатель первого рода, так как невозможно создать машину, которая производит работу без подведения энергии извне.

Первое начало термодинамики имеет огромное философское значение, ибо, утверждая неуничтожимость энергии, оно тем самым обосновывает и неуничтожимость материи, поскольку энергия без материи существовать не может.

Первое начало термодинамики выражается уравнением

Q = ΔU + A , (1.13 )

где ∆U – изменение внутренней энергии.

1. p-const ∆U = Q - A;

2. V-const ∆U = Q.

Для растворов концентрация С:

C = или V = , ( 1.14)

где V – объем.

Долгое время было принято считать тепловые эффекты реакций, проходящих с выделением теплоты, положительными, а с поглощением теплоты — отрицательными, обозначая их соответственно + Q и – Q. В настоящее время в термохимии для единообразия с термодинамикой тепловые эффекты реакции обозначают через подчеркивая этим, что тепловой эффект вызван изменением параметров системы. Поэтому и говорят обычно не о тепловом эффекте, а об изменении энтальпии . Разумеется, если в ходе реакции теплота выделяется (+Q), то энтальпия при этом уменьшается (-), и наоборот, если в ходе процесса теплота поглощается (—Q), то энтальпия системы увеличивается. Таким образом, энтальпия связана с тепловым эффектом реакции зависимостью: Q_p = . Разумеется, если в ходе реакции теплота выделяется (+Q), то энтальпия при этом уменьшается (-), и наоборот, если в ходе процесса теплота поглощается (—Q), то энтальпия системы увеличивается. Таким образом, энтальпия

тепловому эффекту реакции с обратным знаком.

Энтальпия по определению

H= U + pV. (1.15 )

Примеры решения задач

Задача 1

Найти работу расширения 10 г азота от объема 6 м³ до 40 м³ при постоянной температуре, равной 25⁰С.

Решение:

Используем соотношение ( 1.7), так как T – const и изменяется объем:

A= RT ln

Обязательно все данные задачи должны быть в одной системе единиц, (как правило, используйте СИ). Для перевода используем таблицу из приложения (см. с. 63).

m _{N 2} = 1·10^-2 кг, М= 2,8 · 10^-2 кг/кмоль, Т= 273 + 25 = 298К,

где М – масса одного моля.

Моль – количество вещества, выраженное в граммах и численно равное атомной или молекулярной массе.

Для азота (N₂₎ атомная масса А = 14, следовательно, М = 2 ·14 г = 28 г,

так как молекула азота состоит из двух атомов. В системе СИ m – в кг,

поэтому М в кг/кмоль и R = 8,31 · 10³ Дж/ кмоль · град.

2,303 lgA = ln A – соотношение между натуральным и десятичным

логарифмом числа:

A = ln = 24763,8 ⋅ 2,303 ⋅ lg 6,67 = 46993,6 = 4,710 ⁴

Размерность A =

Задача 2

Какая работа будет совершена 5 кг метана при повышении температуры на 500С и постоянном давлении.

Решение

Из условия задачи P – const, поэтому используем уравнение:

A = p (V₂ − V₁ ) = p V₂ − p V₁

Из уравнения: РV₂ = RТ₂, РV₁ = RТ₁

A= R (T₂ − T₁) ;

m = 5 кг, М=16 кг/кмоль (см. задачу 1.)

Т – Т = ∆ Т = 50 К (величины К и °С одинаковы, поэтому ∆Т в К = ∆ °С);

A = = 1,3  10 ⁵

Размерность A =

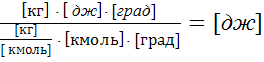
Задача 3

Найти работу изобарического расширения аргона от 2 л до 3 л под давлением 30 Па.

Решение

Из условия задачи p – const . Поэтому используем формулу (1.3):

A = p (V₂ – V₁ ) .

Переводим данные задачи в систему СИ:

2 л = 2 · 10^-3 м, 3 л = 3 · 10^-3 м³, 1 ПА = Н/м², 30 ПА = 30 Н/м².

А = 30 (3·10^-3 - 2·10^-3) = 30 · 10^-3 = 0,03.

Размерность [Н · м^--2 ] · [м³] = [Н] · [м] = [дж].

Задача 4

Найти работу, полученную при изотермическом расширении 100 г

азота при изменении давления от 3·10⁵ Па до 2·10⁵ Па при температуре 70 °С.

Решение

Из условия задачи T – const и меняется давление, поэтому используем формулу 1.5:

A= RT ln

m = 0,1 кг, М= 28 кг/кмоль, T = 273 + 70 °С = 343,

R = 8,31·10³ Дж/кмоль·град,

р₁ = 3·10⁵ Па = 3 ·10⁵ Н/м², p₂ = 2 · 10⁵ Па (Н/м²),

A =  lg = 4126

Размерность A =

Задача 5

10 л кислорода, взятого при нормальных условиях, нагревают до

200⁰С при постоянном объеме. Определить количество теплоты, затраченное на нагревание.

Решение

По условию V = const, поэтому используем формулу (1.6):

Q_V = C_V (T₂ −T₁ ), С_v = R, так как молекула кислорода двухатомная.

Следствие из закона Авогадро. Один моль любого газа при нормальных условиях (0⁰С или 273 К, р = 1 атм или 760 мм. рт. ст. или 1,013·10⁵ Н/м²) занимает объем, равный 22,4 л.

Поэтому = ;

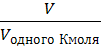T₁ = 273 K; T₂ = 473 K; С_v = R; 10 л = 1 · 10^-2 м³; 1 кмоль = 22,4 м^3.

Q = 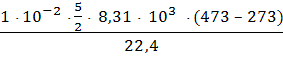= 1855.

Размерность Q =

Задача 6

3 кг неона нагреваются при постоянном давлении. Найти изменение энтальпии, если температура повысилась на 100⁰С:

ΔH = Q p = Cp (T₂ −T₁ ) из формулы (1.7),

из формулы (1.8): Cp = C_V + R = R, так как неон подчиняется законам

идеального газа: Т₂ – Т₁ = ∆Т = ∆⁰С = 100 К,

ΔH = 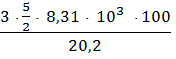= 3,085  10⁵

Размерность ΔH = .

Задача 7

Найти изменение внутренней энергии при испарении 10 г ртути и

давлении 1,013·10⁵ Па. Температура кипения ртути – 357⁰ С. Теплота паро

образования – 1,29·10⁵ Дж/кмоль.

Решение

По условию p – const . Из формулы (1.12) H = U+ pV , ∆U = ∆H – p∆V,

ΔH = Q_фп = λ парообразования .

Пренебрегая объемом жидкой ртути по сравнению с объемом газообразной, получаем

∆V = V газ- V жид ≈ V газ, V = ;

∆U = λ_п − = (λ − RT );

m = 1⋅10 ⁻² кг, М = 107  , р = 1,013 ⋅ 10⁵ ;

R = 8,31 · 10³ Дж/ кмоль · град .

Т = 273 + 357 С = 630К,

ΔU = (1,29 ⋅ 10 − 8,31⋅10³ ⋅ 630) = − 477 Дж.

Размерность ΔU =

Расчет термодинамических потенциалов _ΔG и _ΔH производится с ис­пользованием имеющихся в справочниках и приведенных к стандартным усло­виям значений _ΔS⁰_298K; _ΔG⁰_298K и _ΔН⁰_298K для простых веществ и химических со­единений.

Пример 1. Рассчитать _ΔG⁰_298K и определить возможность протекания сле­дующей реакции при стандартных условиях:

С₂Н₂ (г) + ⁵/₂ O₂ (г) = 2СO₂ (г) + Н₂O + _ΔG_р-ции , если значение _ΔG⁰_298K = 209 (для ацетилена), для углекислого газа _ΔG⁰_298K = -393,3, а для жидкой воды _ΔG⁰_298K = -237 кДж/моль (для кислорода _ΔG⁰_298K = 0).

Решение: _ΔG_р-ции = 2 _ΔG°_298K (СO_{2 (г)} ) + _ΔG⁰_298K (Н₂O _(ж) ) - - _ΔG⁰_298K (С₂Н_{2 (г)}) = 2(-393,3) + (-237) - 209 = -786,6 - 237 - 209 = = -1232,6 кДж/моль. Поскольку полученное значение _ΔG_р-ции < 0, реакция может идти в прямом на­правлении.

Пример 2. Вычислить изменения энтропии образования (_ΔS⁰_обр) этанола из элементов, если (_ΔS⁰_298К) при стандартных условиях для С_(Т) графит = 5,21; Н_2(г)= 130,52; O_2(л) = 205,18; С₂Н₅ОН_(ж)= 160,78 кДж/моль

Решение: _ΔS⁰_образ = Σ_ΔS_298K (продуктов) - Σ_ΔS_298K (реагентов). Уравнение образования этанола из элементов: 2С + 3Н₂ + ¹/₂O₂ = С₂Н₅ОН. Подставляя величины _ΔS⁰_образ = 160,78 - (2×5,21 + 3×130,52 + ¹/₂( 2×205,18) = = -343,79 кДж/моль.

Вопросы для самопроверки

1. Что такое энергия? Перечислите известные вам ее виды, сформулируйте закон сохранения энергии.

2. Что понимается под внутренней энергией термодинамической системы? Что такое энтальпия? Какова связь между внутренней энергией и энтальпией?

3. Сформулируйте первое начало термодинамики. Приведите его математическое выражение. В чем особенности тепловой энергии?

4. Сформулируйте закон Гесса. Укажите условия его применения. Как рассчитывают тепловые эффекты реакций, которые могут быть найдены экс­периментально? Какие данные для этого необходимы?

5. Укажите связь закона Гесса с первым законом термодинамики.

6. Как определяют теплоты реакций из энтальпий образования веществ?

7. Что такое параметр состояния? Какие параметры состояния термодинами­ческой системы являются интенсивными, экстенсивными? перечислите термодинамические параметры, применяющиеся для описания систем, в которых протекает химическая реакция (в том числе и биологических).