2.4 Определители

Рассмотрим квадратную матрицу А порядка n .

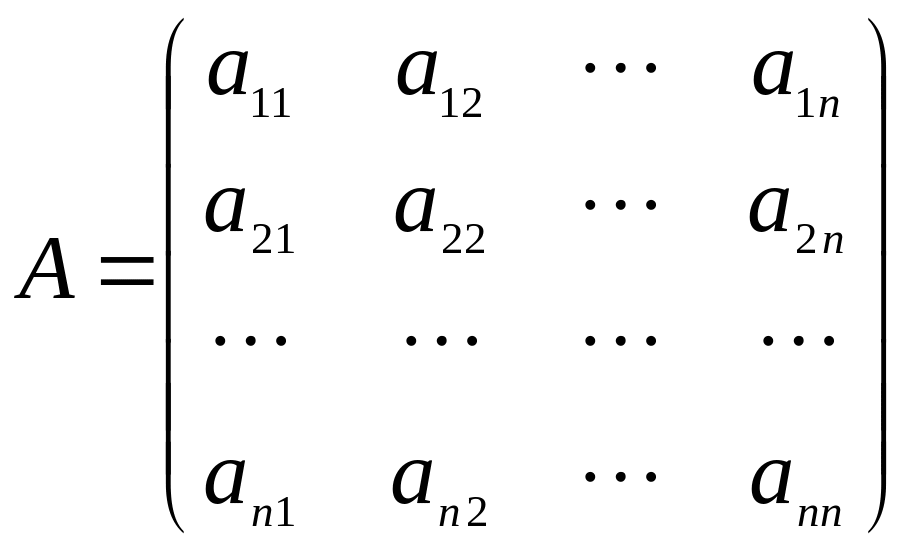С каждой такой матрицей свяжем вполне определенную числовую характеристику, называемую определителем, соответствующую этой матрице.

Определение. Определителем квадратной матрицы второго порядка называется число, равное значению выражения и обозначается .

Прежде чем ввести понятие определителя n-го порядка, введем определения понятий минора и алгебраического дополнения элемента a_ij, для любых i, j.

Определение. Минором M_ij любого элемента a_ij матрицы n-го порядка называется определитель (n-1)-го порядка, соответствующий той матрице, которая получается из исходной матрицы вычеркиванием строки и столбца, на пересечении которых стоит элемент a_ij, т.е. i-й строки и j-го столбца.

Пример 2.7. Найти минор M₂₃ матрицы .

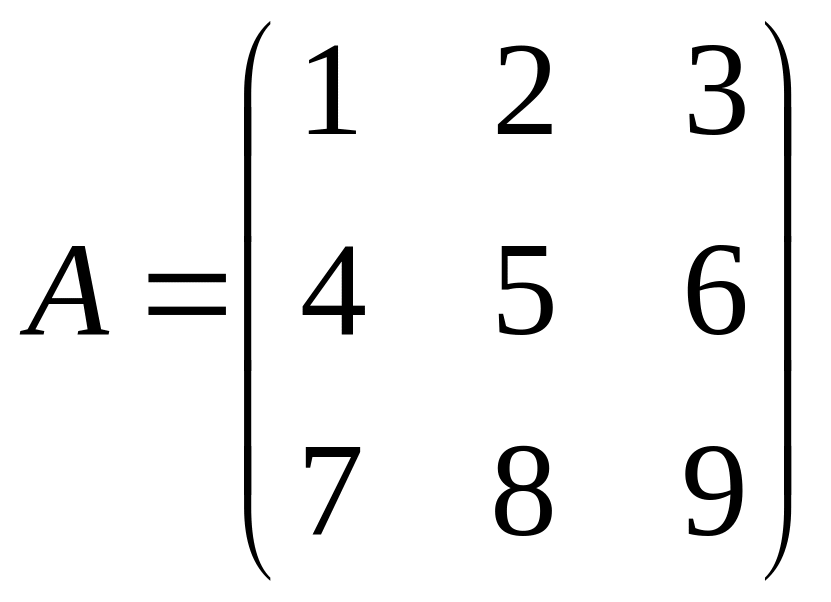Решение. Составим матрицу _, соответствующую элементу , то есть из исходной матрицы вычеркнем элементы второй строки и третьего столбца, остальные элементы образуют матрицу . Найдем определитель матрицы , следовательно, вычислим минор .

Определение. Алгебраическим дополнением A_ij элемента a_ij определителя n - го порядка называется минор M_ij элемента a_ij , умноженный на число (-1)^i+j_.

.

Пример 2.8 Найти алгебраическое дополнение элемента а₂₃ матрицы

.

Решение. Из примера 2.7 известно, что , тогда алгебраическое дополнение элемента будет равно .

Определение. Определитель квадратной матрицы n-го порядка равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения

Вычисление определителя по данной формуле называется разложением определителя по элементам -го столбца (первая сумма) или j-й строки (вторая сумма).

Пример 2.9. Вычислить определитель .

Решение. Поскольку третья строка и второй столбец содержат один элемент, равный нулю, то целесообразно вычисление определителя выполнить, разложив его по третьей строке или по второму столбцу. Тогда получим

Слагаемое с нулевым множителем написано для иллюстрации того, что при вычислении определителя эти слагаемые нужно опускать.

Вычислим этот же определитель, разложив его по третьему столбцу.

Свойства определителей

1) Величина определителя не изменится при транспонировании.

2) Определитель, все элементы некоторой строки которого равны нулю, равен нулю.

3) Величина определителя при перестановке любых двух строк (столбцов) меняет знак на противоположный.

4) Общий множитель некоторой строки (столбца) можно выносить за знак определителя.

5) Если элементы какой-либо строки (столбца) представляются в виде суммы двух слагаемых, то определитель может быть разложен на сумму двух определителей, в первом из которых элементы названной строки (столбца) равны первым слагаемым, во втором - вторым.

6) Величина определителя не изменится, если к элементам любой строки (столбца) прибавить соответствующие элементы любой другой строки (столбца), умноженные на одно и тоже число.

7) Сумма произведений элементов какой-либо строки (столбца) на алгебраические дополнения соответствующих элементов любой другой строки (столбца) равна нулю.

8) Определитель произведения двух квадратных матриц A и B равен произведению их определителей |AB| = |A||B|

Свойства определителей используются при вычислении определителей (в особенности свойство 6).

Пример 2.10. Вычислить определитель матрицы четвёртого порядка

.

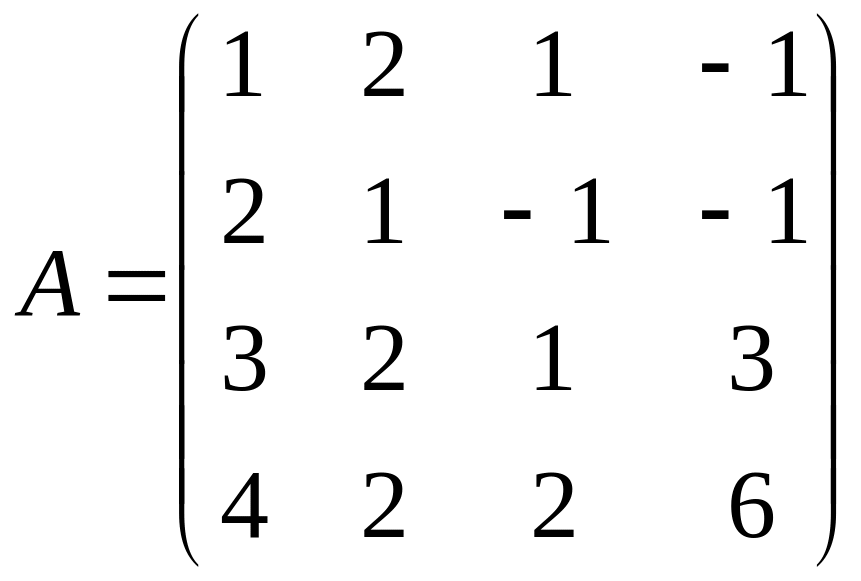Решение. Используя свойство 6, обеспечим, чтобы в третьем столбце элемент первой строки остался равным 1, а остальные элементы этого столбца сделаем равными 0.

Для этого выполним следующие действия:

- первую строку оставляем без изменения;

- ко второй строке прибавим первую строку и запишем во второй строке;

- из третьей строки вычтем первую строку и запишем в третьей строке;

- из четвертой строки вычтем удвоенную первую и запишем в четвертой строке.

В результате получим .

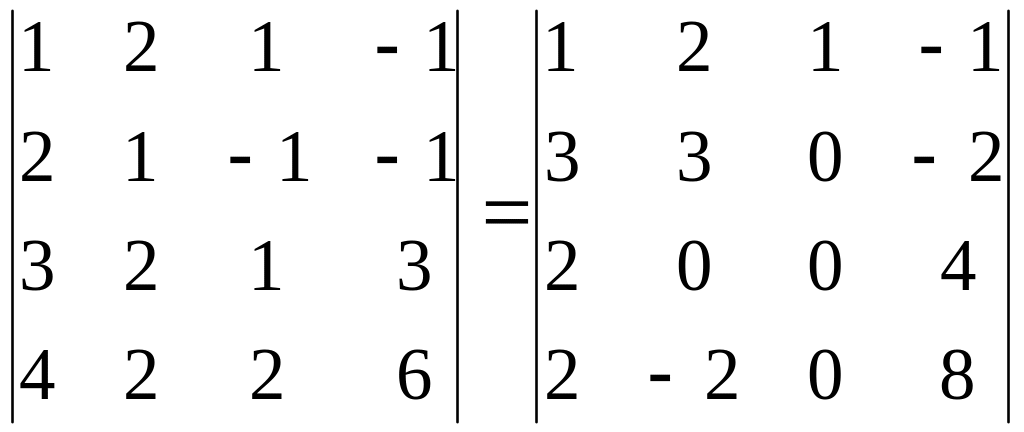Вынесем общий множитель из третьей и четвертой строк за знак определителя по свойству 4 .

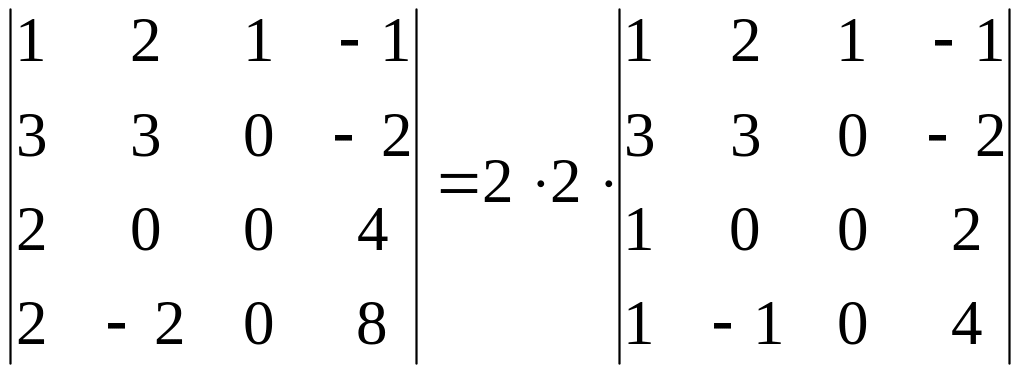Далее, разложив по элементам 3 столбца, получим

.

Применяя свойство 6, к элементам первой строки прибавим третью строку, умноженную на 3 и запишем в первой строке, а вторую и третью строки определителя оставим без изменения

.

Раскладывая по элементам 2 столбца, вычислим определитель исходной матрицы .

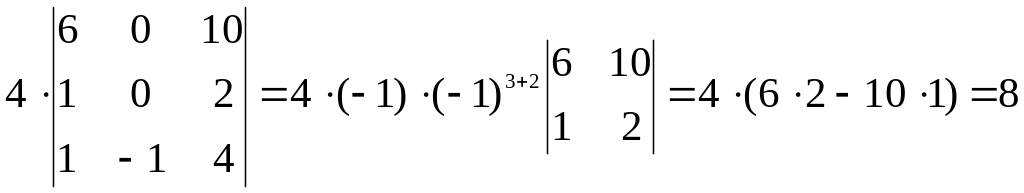Замечание 1. Вычисление определителя матрицы четвёртого порядка разложением по элементам любой строки или столбца требует вычисления четырех определителей третьего порядка; для нахождения значения каждого определителя третьего порядка следует вычислить три определителя второго порядка. Общее число определителей, которые нужно вычислить, можно сократить. Для этого, используя свойство 6, необходимо преобразовать определитель к определителю, у которого какая-либо строка или столбец состоят из нулевых элементов кроме одного.

Замечание 2. Для нахождения определителя третьего порядка используется правило Саррюса

.
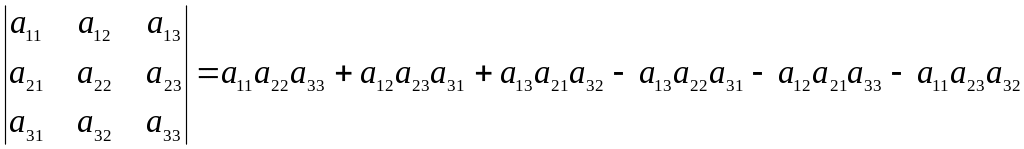