
- •Линейная алгебра
- •2.6 Упражнения для самостоятельной работы 29
- •3.7 Упражнения для самостоятельной работы 76
- •4.4 Упражнения для самостоятельной работы 111
- •Введение
- •1 Комплексные числа
- •1.1 Определение и различные формы записи комплексного числа
- •1.2 Действия над комплексными числами в алгебраической форме
- •1.3 Действия над комплексными числами в тригонометрической форме
- •1.4 Извлечение корня n-ой степени из комплексных чисел
- •1.5. Упражнения для самостоятельной работы
- •1.6. Тест по теме «Комплексные числа»
- •2 Матрицы и определители
- •2.1 Понятие о матрице
- •2.2 Виды матриц
- •2.3 Операции над матрицами
- •2.4 Определители
- •2.5 Обратная матрица
- •Алгоритм построения обратной матрицы
- •2.6 Упражнения для самостоятельной работы
- •2.7 Тест по теме «Матрицы и определители»
- •Контрольная работа по теме «Комплексные числа» и «Матрицы»
- •Образец решения контрольной работы по теме «Комплексные числа» и «Матрицы»
- •3 Системы линейных алгебраических уравнений
- •3.1 Основные понятия
- •3.2 Теорема Кронекера-Капелли
- •3.3 Решение произвольной системы линейных алгебраических уравнений
- •3.3.1 Матричное решение системы уравнений
- •3.3.2 Правило Крамера
- •3.3.3 Элементарные преобразования системы линейных алгебраических уравнений
- •3.3.4 Метод Гаусса (Метод последовательного исключения неизвестных)
- •3.3.5 Метод Жордана-Гаусса
- •3.4 Однородная система линейных уравнений
- •3.5 Метод Жордана обращения матрицы
- •3.6 Системы линейных алгебраических уравнений в программе Mathcad
- •2 Способ - использование встроенной функции lsolve
- •Решить систему уравнений методом Гаусса
- •3.7 Упражнения для самостоятельной работы
- •2) Решить задачи, используя все методы решения системы уравнений.
- •3.8 Тест по теме «Системы линейных алгебраических уравнений»
- •Контрольная работа по теме «Системы линейных алгебраических уравнений»
- •4 Векторное пространство
- •4.2 Линейная зависимость векторов
- •4.3 Элементы векторной алгебры
- •4.3.1Понятие системы координат
- •4.3.2 Декартова система координат
- •Пусть заданы векторы в прямоугольной системе координат тогда линейные операции над ними в координатах имеют вид
- •4.3.3 Скалярное произведение векторов
- •4.3.4 Векторное произведение векторов
- •4.3.5 Смешанное произведение векторов
- •Свойства смешанного произведения векторов
- •4.4 Упражнения для самостоятельной работы
- •4.5.Контрольная работа по теме «Векторное пространство»
- •Образец решения контрольной работы
- •Библиографический список
1.2 Действия над комплексными числами в алгебраической форме
Складывая и вычитая выражения и как обычные многочлены, получим комплексные числа
![]() и
и
![]() .
.
Их
называют соответственно суммой и
разностью чисел
и
(обозначают
![]() и
и
![]() ).
Аналогично, умножая
и
как обычные многочлены и учитывая, что
,
получим
).
Аналогично, умножая
и
как обычные многочлены и учитывая, что
,
получим
![]() .
.
Комплексное
число в правой части формулы называют
произведением комплексных чисел
и
(обозначают
![]() ).
Произведение
).
Произведение
![]() комплексных чисел, равных
,
называют
–й
степенью числа
и обозначают
комплексных чисел, равных
,
называют
–й
степенью числа
и обозначают
![]() .
.
Пример
1.3 Даны комплексные числа
![]() ,
,
![]() .
Найти сумму, разность, произведение
этих чисел, число
возвести в 3 степень.
.
Найти сумму, разность, произведение
этих чисел, число
возвести в 3 степень.
Решение.
1)
Сумма чисел
![]() .
.
2)
Разность чисел
![]() .
.
3) Произведение чисел
![]() .
.
4)
![]() .
.
Введенные выше операции сложения и умножения комплексных чисел обладают теми же свойствами, что сложение и умножение действительных чисел. Легко убедиться в справедливости следующих равенств:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() .
.
Замечание.
Комплексному числу
на комплексной плоскости ставится в
соответствие точка
.
Однако, можно поставить ему в соответствие
и радиус-вектор
![]() .
Такое соответствие тоже является взаимно
однозначным, причем в этом случае
операции сложения и вычитания комплексных
чисел естественны с геометрической
точки зрения.
.
Такое соответствие тоже является взаимно
однозначным, причем в этом случае
операции сложения и вычитания комплексных
чисел естественны с геометрической
точки зрения.
Действительно,
сумме
![]() соответствует вектор
соответствует вектор
![]() (где
(где
![]() ,
,
![]() ),
а разности
),
а разности
![]() соответствует вектор
соответствует вектор
![]() .
.
Операцию
деления комплексных чисел вводят как
обратную умножению: комплексное число
![]() называется частным чисел
и
называется частным чисел
и
![]() (обозначают
(обозначают
![]() ),
если
),
если
![]() .
.
Пусть
,
и
![]()
![]() .
Тогда
.
Тогда
![]() .
.
Из
уравнений ![]() и
и
![]() находим
находим
![]() и
и
![]() .
.
Таким
образом,
![]()
![]() .
.
Замечание.
Тот же результат формально получится,
если числитель и знаменатель дроби
![]() умножить на число, сопряженное знаменателю,
т.е. на
умножить на число, сопряженное знаменателю,
т.е. на
![]() .
.
![]()
![]() .
.
В практических вычислениях пользуются именно этим приемом.
Пример 1.4 Даны числа , , найти их частное.
Решение.
![]() .
.
1.3 Действия над комплексными числами в тригонометрической форме
Умножение и деление комплексных чисел проще выполнять, если они записаны в тригонометрической форме. Действительно, пусть комплексные числа и заданы в тригонометрической форме
![]() ,
,
![]() .
.
Перемножив их, получим
![]()
![]() .
.
Откуда, используя формулы косинуса и синуса суммы, находим
![]() .
.
Итак, при умножении комплексных чисел их модули перемножаются, а аргументы – складываются.
Формула
является верной для любого конечного
числа множителей. В частности, при
возведении числа
в степень
(![]() )
получим
)
получим ![]() .
.
Последнее выражение называют формулой Муавра.
Теперь разделим на . Получим
![]()
![]() .
.
Но
![]() ,
следовательно,
,
следовательно,
![]()
![]() .
.
Используя формулы для косинуса и синуса разности, находим
![]() .
.
Итак,
при делении
на
получили комплексное число, модуль
которого равен частному
![]() ,
а аргумент – разности (
,
а аргумент – разности (![]() ).
).
Пример
1.5. Даны числа
![]() ,
,
![]() .
Найти их произведение, частное, число
возвести в 5 степень.
.
Найти их произведение, частное, число
возвести в 5 степень.
Решение.
Произведение
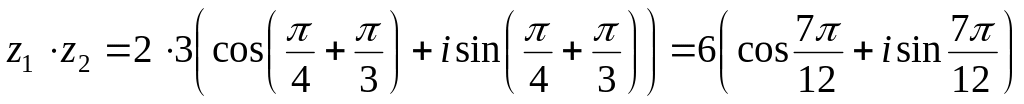 .
.Частное
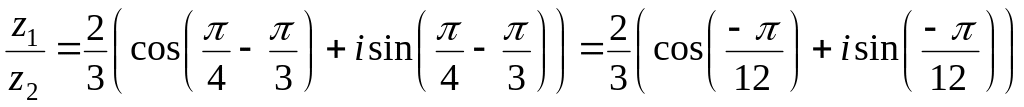 .
.Возведение в степень
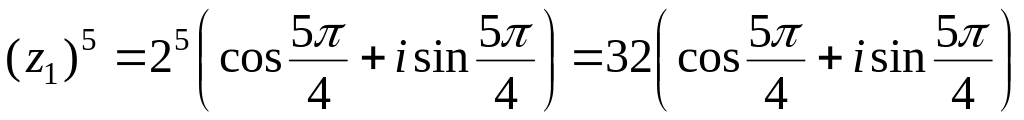 .
.
1.4 Извлечение корня n-ой степени из комплексных чисел
Определение.
Пусть
– натуральное число. Корнем
–ой
степени из комплексного числа
(обозначают
![]() )
называют комплексное число
)
называют комплексное число
![]() ,
такое, что
,
такое, что
![]() .
.
Пусть
![]() ,
,
![]() .
Тогда получаем
.
Тогда получаем
![]() .
Отсюда
.
Отсюда
![]() ,
,
![]() ,
следовательно
,
следовательно![]() .
.
Таким образом, все корни –ой степени из комплексного числа могут быть найдены по формуле
![]() , где
, где
![]() .
.
Замечание.
Формально
![]() в последней формуле может принимать
любое целое значение. Но угол
в последней формуле может принимать
любое целое значение. Но угол
![]() и угол
и угол
![]() различаются на величину
различаются на величину
![]() .
Следовательно, при
и
.
Следовательно, при
и
![]() получается одно и то же комплексное
число. Таким образом, различных значений
корня будет только
,
чтобы их найти достаточно взять
.
получается одно и то же комплексное
число. Таким образом, различных значений
корня будет только
,
чтобы их найти достаточно взять
.
Пример
1.6. Найти все значения
![]() .
.
Обозначим
значения
через
![]() .
Чтобы найти
необходимо сначала записать комплексное
число
.
Чтобы найти
необходимо сначала записать комплексное
число
![]() в тригонометрической форме. Имеем
в тригонометрической форме. Имеем ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Теперь находим
![]()
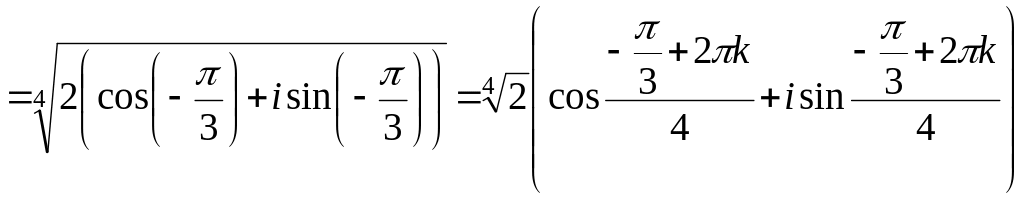 ,
,
где
![]() .
Или, более подробно,
.
Или, более подробно,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
