
- •Линейная алгебра
- •2.6 Упражнения для самостоятельной работы 29
- •3.7 Упражнения для самостоятельной работы 76
- •4.4 Упражнения для самостоятельной работы 111
- •Введение
- •1 Комплексные числа
- •1.1 Определение и различные формы записи комплексного числа
- •1.2 Действия над комплексными числами в алгебраической форме
- •1.3 Действия над комплексными числами в тригонометрической форме
- •1.4 Извлечение корня n-ой степени из комплексных чисел
- •1.5. Упражнения для самостоятельной работы
- •1.6. Тест по теме «Комплексные числа»
- •2 Матрицы и определители
- •2.1 Понятие о матрице
- •2.2 Виды матриц
- •2.3 Операции над матрицами
- •2.4 Определители
- •2.5 Обратная матрица
- •Алгоритм построения обратной матрицы
- •2.6 Упражнения для самостоятельной работы
- •2.7 Тест по теме «Матрицы и определители»
- •Контрольная работа по теме «Комплексные числа» и «Матрицы»
- •Образец решения контрольной работы по теме «Комплексные числа» и «Матрицы»
- •3 Системы линейных алгебраических уравнений
- •3.1 Основные понятия
- •3.2 Теорема Кронекера-Капелли
- •3.3 Решение произвольной системы линейных алгебраических уравнений
- •3.3.1 Матричное решение системы уравнений
- •3.3.2 Правило Крамера
- •3.3.3 Элементарные преобразования системы линейных алгебраических уравнений
- •3.3.4 Метод Гаусса (Метод последовательного исключения неизвестных)
- •3.3.5 Метод Жордана-Гаусса
- •3.4 Однородная система линейных уравнений
- •3.5 Метод Жордана обращения матрицы
- •3.6 Системы линейных алгебраических уравнений в программе Mathcad
- •2 Способ - использование встроенной функции lsolve
- •Решить систему уравнений методом Гаусса
- •3.7 Упражнения для самостоятельной работы
- •2) Решить задачи, используя все методы решения системы уравнений.
- •3.8 Тест по теме «Системы линейных алгебраических уравнений»
- •Контрольная работа по теме «Системы линейных алгебраических уравнений»
- •4 Векторное пространство
- •4.2 Линейная зависимость векторов
- •4.3 Элементы векторной алгебры
- •4.3.1Понятие системы координат
- •4.3.2 Декартова система координат
- •Пусть заданы векторы в прямоугольной системе координат тогда линейные операции над ними в координатах имеют вид
- •4.3.3 Скалярное произведение векторов
- •4.3.4 Векторное произведение векторов
- •4.3.5 Смешанное произведение векторов
- •Свойства смешанного произведения векторов
- •4.4 Упражнения для самостоятельной работы
- •4.5.Контрольная работа по теме «Векторное пространство»
- •Образец решения контрольной работы
- •Библиографический список
4.2 Линейная зависимость векторов
Рассмотрим k
n-мерных векторов
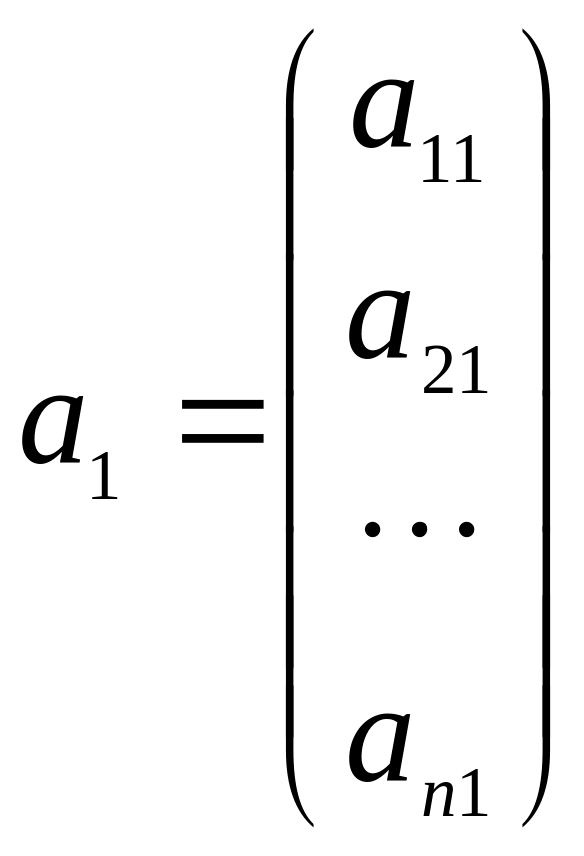 ,
,
 ,
…,
,
…,

Определение.
Линейной комбинацией векторов
![]() с коэффициентами соответственно
с коэффициентами соответственно
![]() называется вектор
называется вектор
![]() .
.
Пример 4.2.
Даны векторы
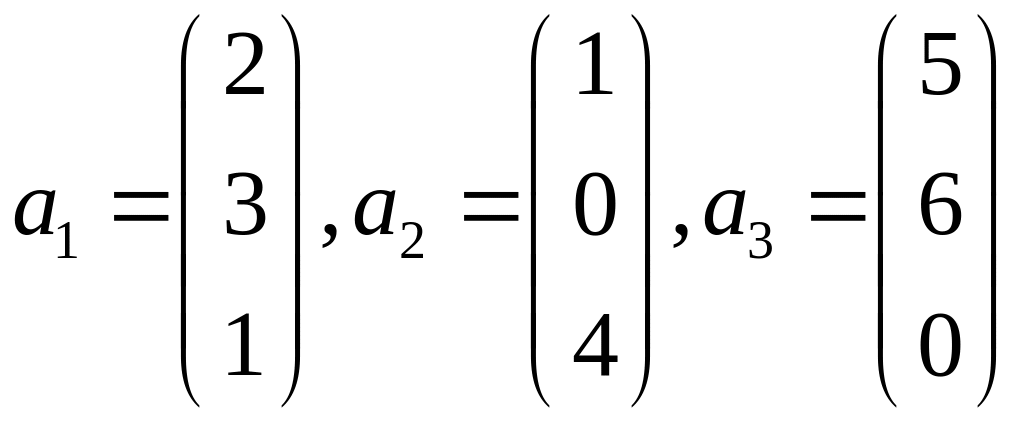 .
Найти линейную комбинацию этих векторов
с коэффициентами
.
Найти линейную комбинацию этих векторов
с коэффициентами
![]() ,
,
![]() ,
,
![]() .
.
Решение. Согласно определению получаем
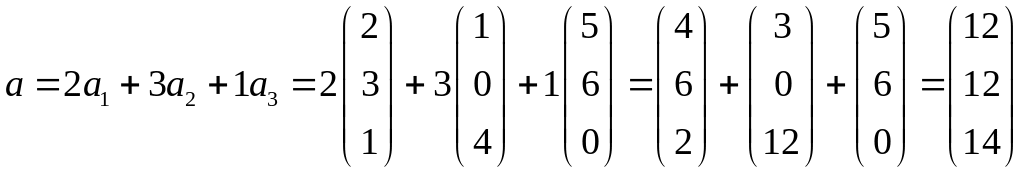 .
.
Определение.
Система векторов
![]() называется линейно зависимой, если
существуют такие числа
,
не все равные нулю, что линейная комбинация
векторов с этими коэффициентами равна
нулевому вектору, то есть
называется линейно зависимой, если
существуют такие числа
,
не все равные нулю, что линейная комбинация
векторов с этими коэффициентами равна
нулевому вектору, то есть
![]() .
.
Определение.
Система векторов
![]() называется линейно независимой,
если равенство
возможно тогда и только тогда, когда
все коэффициенты
равны нулю.
называется линейно независимой,
если равенство
возможно тогда и только тогда, когда
все коэффициенты
равны нулю.
Теорема. Для того чтобы система векторов была линейно независимой необходимо и достаточно, чтобы хотя бы один вектор из этой системы можно было представить в виде линейной комбинации остальных.
Доказательство.
Необходимость.
Пусть векторы
линейно зависимы. Тогда по определению
линейной зависимости векторов получаем,
что существует такая система чисел
, среди которых имеется хотя бы одно не
равное нулю, что выполняется равенство:
![]() .
Пусть число
.
Пусть число
![]() не равно нулю. Из левой части полученного
векторного равенства все слагаемые
кроме вектора
не равно нулю. Из левой части полученного
векторного равенства все слагаемые
кроме вектора
![]() перенесем в правую часть, получим
равенство:
перенесем в правую часть, получим
равенство:
![]() ,
из которого следует, что вектор
есть линейная комбинация векторов
,
из которого следует, что вектор
есть линейная комбинация векторов
![]() .
.
Достаточность.
Пусть какой-нибудь вектор, например
,
системы векторов
является линейной комбинацией остальных
векторов. Перенесем все слагаемые из
одной части в другую. Получим векторное
равенство:
![]() ,
из которого следует, что векторы
линейно зависимы. Теорема доказана.
,
из которого следует, что векторы
линейно зависимы. Теорема доказана.
Свойства линейной зависимости векторов.
1. Если система векторов содержит хотя бы один нулевой вектор, то она линейно зависима.
2. Если какая-нибудь подсистема системы векторов линейно зависима, то и вся система векторов тоже линейно зависима.
3. Если система векторов линейно независима, то и любая ее подсистема тоже линейно независима.
Рассмотрим систему n-мерных векторов .
Определение. Любая совокупность (подсистема) векторов из системы векторов называется базисом данной системы, если выполняются условия:
векторы этой совокупности (подсистемы) линейно независимы;
любой вектор системы является линейной комбинацией векторов этой подсистемы.
Пример 4.3. Доказать, что одним из базисов системы векторов
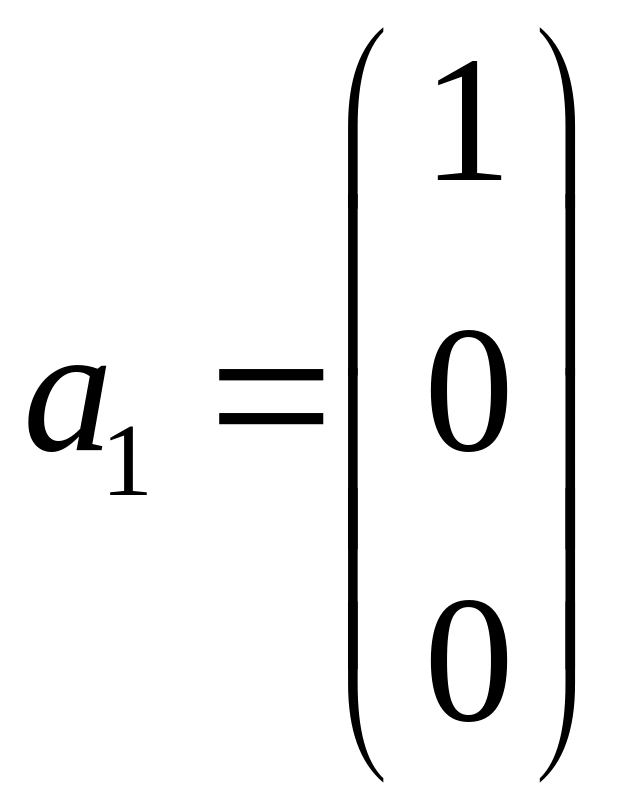 ,
,
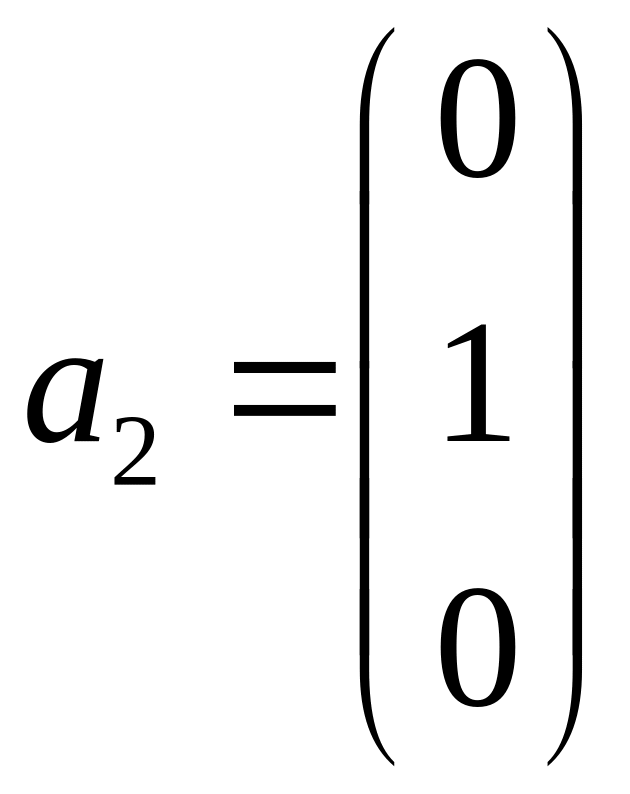 ,
,
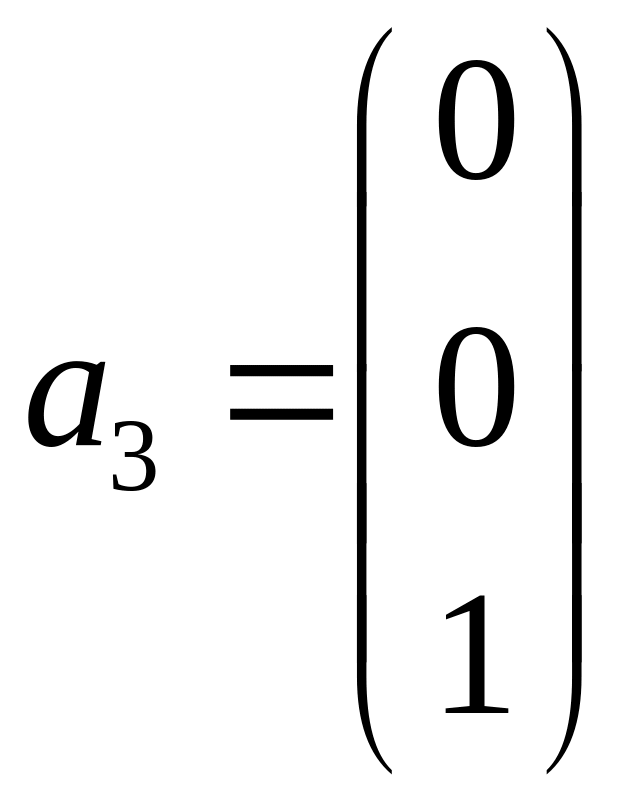 ,
,
 ,
,
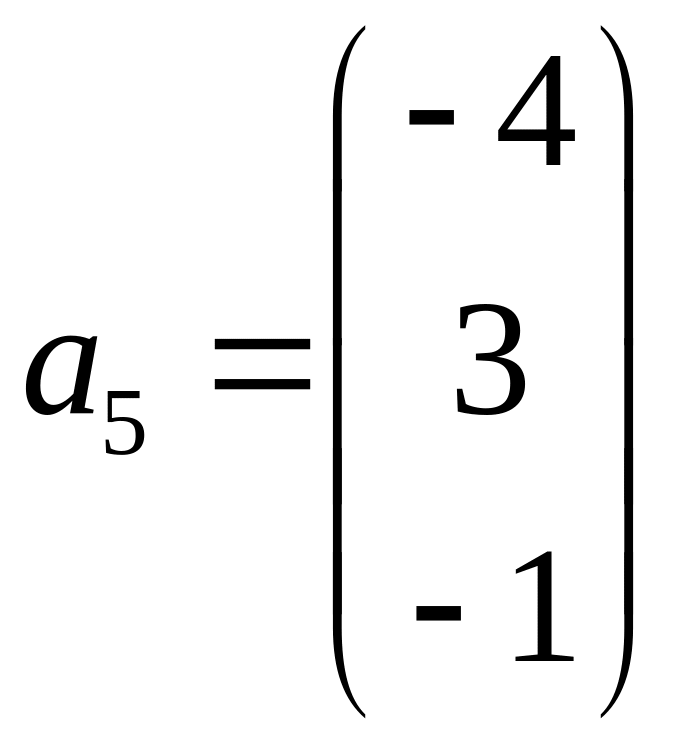 является подсистема, состоящая из
векторов
является подсистема, состоящая из
векторов
![]() .
.
Доказательство. Проверим линейную независимость подсистемы векторов , для этого составим линейную комбинацию этих векторов
 ,
таким образом, вектор
,
таким образом, вектор
![]() будет нулевым, если все его компоненты
равны нулю
будет нулевым, если все его компоненты
равны нулю
![]() .
.
Следовательно,
векторы
![]() линейно независимы.
линейно независимы.
Любой вектор
системы
![]() можно представить в виде линейной
комбинации векторов
можно представить в виде линейной
комбинации векторов
![]() ,
,
![]() ,
,
![]() ,
,
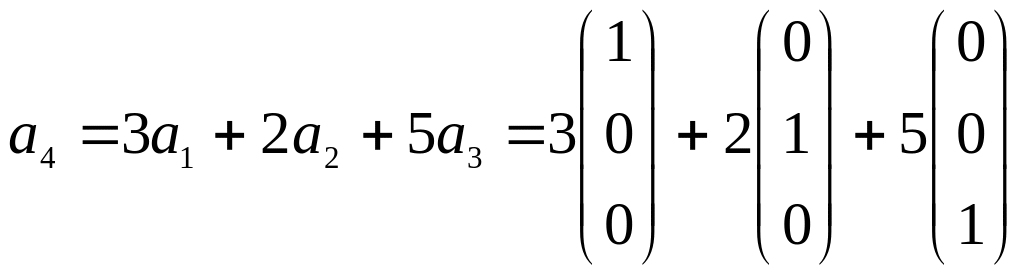 ,
,
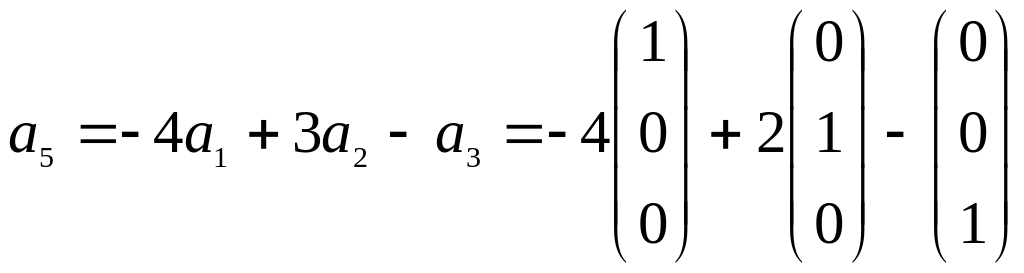 .
.
Согласно определению, векторы образуют базис данной системы векторов .
Определение. Векторы, составляющие базис системы векторов, называются базисными.
Говоря вообще,
система векторов может иметь различные
базисы. Например, в примере 4.2, кроме
базисных векторов
,
базисами данной системы векторов
являются также подсистемы
![]() ,
,
![]() и другие. Причём все базисы данной
системы векторов состоят из одного и
того же числа базисных векторов.
и другие. Причём все базисы данной
системы векторов состоят из одного и
того же числа базисных векторов.
Определение. Число базисных векторов данной системы векторов называется рангом этой системы. Другими словами, рангом системы векторов называется максимальное число линейно независимых векторов системы.
Ранг системы нулевых векторов равен 0.
