3.3.5 Метод Жордана-Гаусса

Пусть задана система линейных алгебраических уравнений

                                 (3.6)

Подвергая систему линейных алгебраических уравнений элементарным преобразованиям, можно любую неизвестную исключить из всех уравнений, кроме какого-нибудь одного уравнения.

Пусть в системе (3.6) коэффициент и необходимо исключить неизвестную из всех уравнений, кроме -го. Будем называть элемент разрешающим коэффициентом, - разрешающей неизвестной, -е уравнение - разрешающим уравнением. Умножим -е уравнение на число и прибавим к -му уравнению.

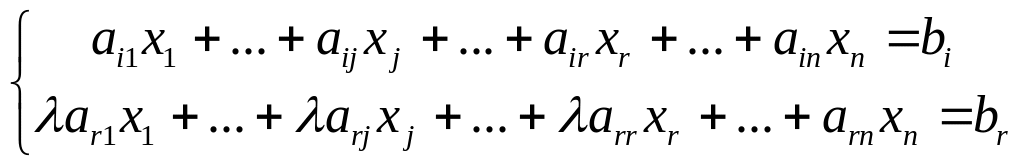
Получим уравнение

Выберем число так, чтобы коэффициент при в -м уравнении был равен нулю, то есть

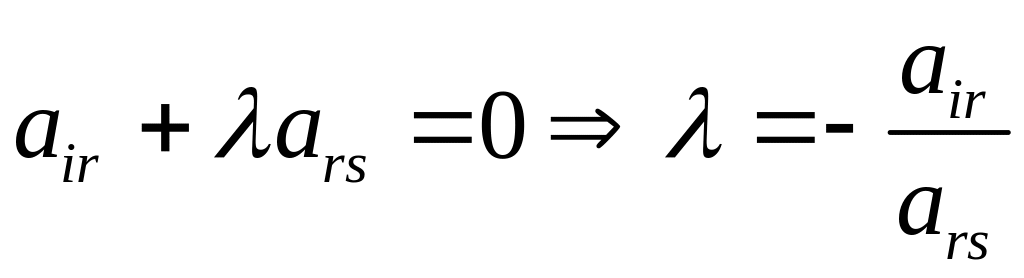
Подставляя значение в последнее уравнение, исключим переменную из -го уравнения, остальные коэффициенты будут равны (новые значения коэффициентов обозначаются со штрихами)

, , …,      (3.7)

Формулы (3.7) называются формулами исключения. Запись новых значений коэффициентов в виде 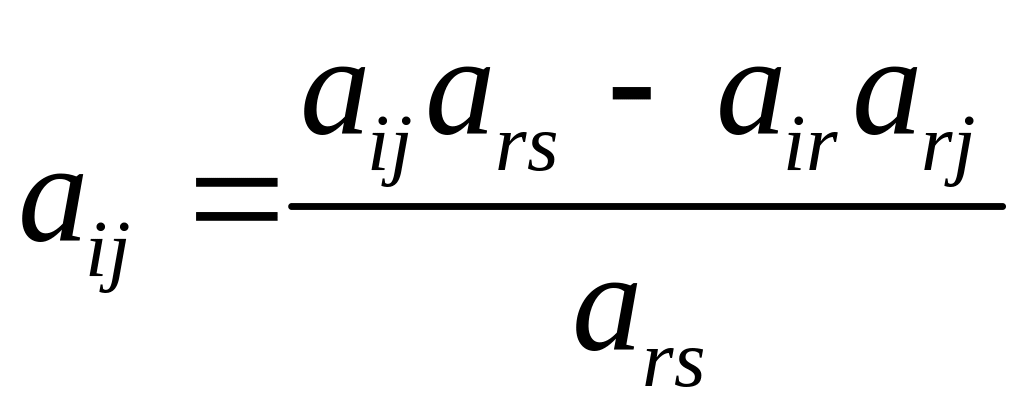позволяет сформулировать формулы исключения в виде правила прямоугольника: новое значение коэффициента равно дроби, знаменатель которой равен , а числитель - разности произведений элементов, стоящих в противоположных вершинах прямоугольника, построенного по строкам и столбцам на элементах и _j, причем вычитается произведение элементов не содержащее разрешающего элемента.

a _ij ... a_is

. .

a_rj …

Метод Жордана-Гаусса при решении систем линейных алгебраических уравнений применяет формулы исключения и элементарные преобразования.

Так как в процессе преобразований системы изменяются только коэффициенты и правые части уравнений, то можно процедуру исключения проводить по таблицам (расширенной матрице системы).

Правила решения

1. Выбирается разрешающий элемент (любой элемент таблицы, за исключением элементов столбца свободных членов). Разрешающий элемент не должен быть равным нулю.

2. Строка, в которой стоит разрешающий элемент, делится на разрешающий элемент. Остальные строки преобразуются с помощью элементарного преобразования или с помощью формул исключения (правило прямоугольника). Элементы столбца пересчитываются в соответствии с этими правилами.

3. Заполняется новая таблица.

Пример 3.7. Решить методом Жордана -Гаусса систему уравнений

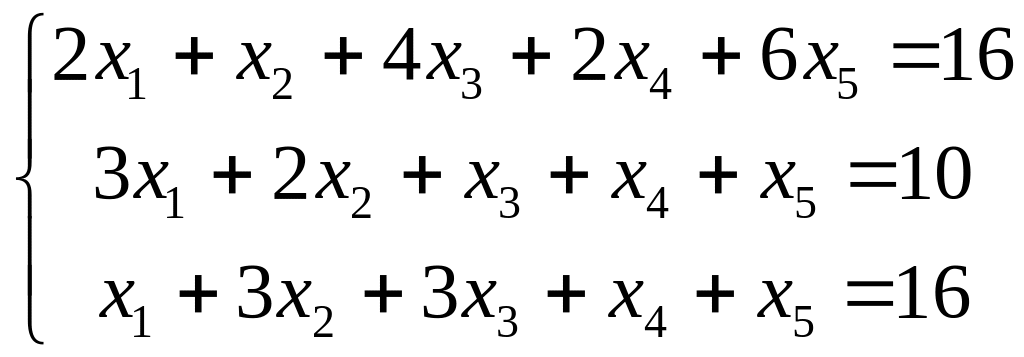
Решение. Запишем систему в виде следующей таблицы

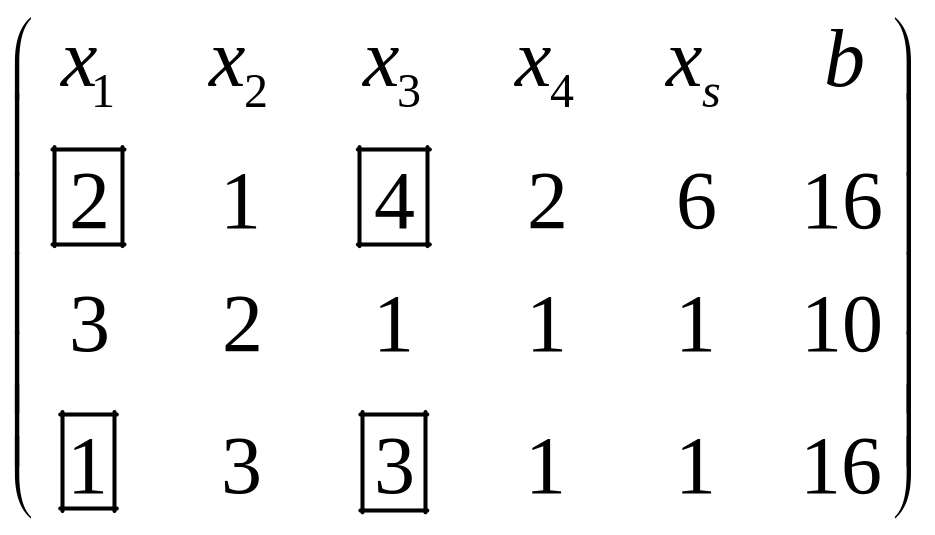
На первом шаге за разрешающий элемент можно взять любой из основной матрицы (без столбца) свободных членов, так как они все отличны от нуля.

Возьмем элемент 2 в первой строке и первом столбце. В таблице разрешающий элемент помечен (обведен квадратом).

Строим новую таблицу: элементы первой строки получаются из элементов первой строки старой таблицы путем деления их на разрешающий элемент. Система уравнений примет вид

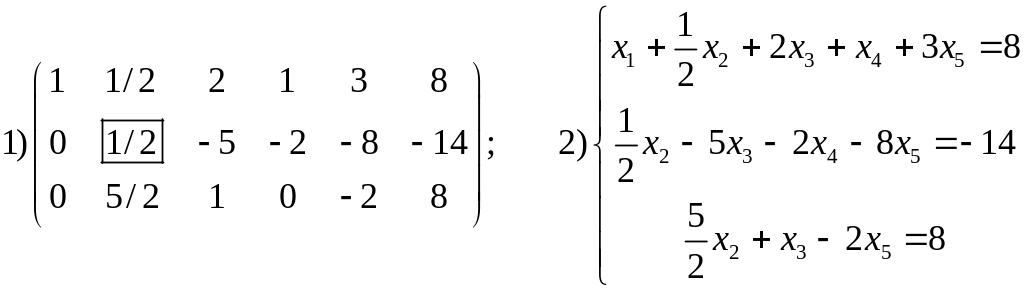
(справа от таблицы выписана система уравнений, соответствующая таблице).

Во всех строках первого столбца, кроме первой, пишем нули, так как разрешающая неизвестная будет исключена из всех уравнений, кроме первого.

Остальные элементы пересчитываем или с помощью элементарного преобразования или по формулам исключения (правило прямоугольника).

Допустим, надо найти элемент третьей строки и третьего столбца. Помечаем соответствующий элемент в старой таблице (обведен квадратом). Далее по строкам и столбцам таблицы помечаем элементы еще двух вершин прямоугольника (они обведены треугольниками).

Таким образом, вершины прямоугольника указаны все. Перемножим элементы противоположных вершин и вычисляем новое значение третьей строки и третьего столбца новой таблицы

.

Число 1 пишем в третьей строке и третьем столбце.

Подчеркнем, что в числителе из произведения, содержащего разрешающий элемент, вычитается произведение элементов в двух остальных вершинах прямоугольника.

Аналогично пересчитываются и остальные элементы таблицы.

В новой таблице снова выбирается разрешающий элемент и алгоритм повторяется. (Этот элемент берётся в отличной от ранее выбранной строке.)

В таблице снова выбирается разрешающий элемент (во второй строке и втором столбце, т.е. ), пересчитывается таблица по тем же правилам и строится новая. Алгоритм имеет конечное число шагов.

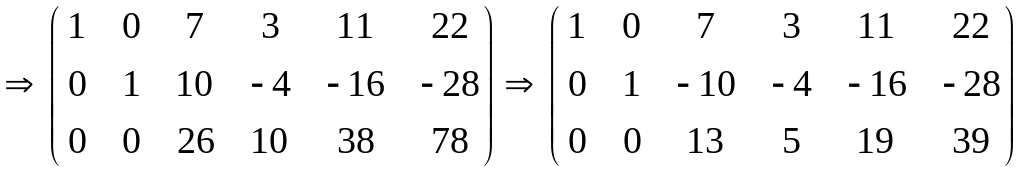
(В данном случае для упрощения расчетов применим преобразование: умножим третью строку на число ).

Снова выбираем разрешающий элемент 13 и пересчитываем таблицу

Общее решение имеет вид

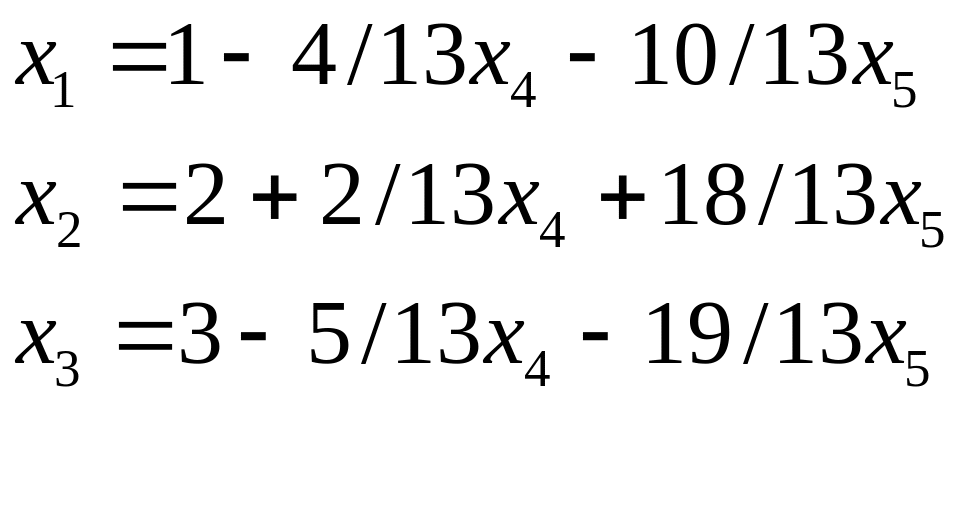
Частное решение для х4=х5=13 равно	Базисное решение для