Глава 2. Функции и их свойства.

§ 1. Понятие функции и её основные свойства.

. Понятие функции. Область определения и множество значений.

Определение: Функцией y = f(x) называется зависимость одной переменной от другой, при которой каждому значению независимой переменной x соответствует единственное значение зависимой переменной y. Независимая переменная называется также аргументом функции, а зависимая – собственно функцией.

Иногда удобно следующая формулировка: функцией f: АВ называется такое отображение множества A в B, при котором каждому элементу множества A соответствует единственный элемент множества B.

f – функция А В		f – функция А В
g x4 А В g – не функция (так как элементу x4 A не соответствует ни один элемент из множества В)		h x1 x2 y А В h – не функция ( так как нарушена единственность образа: x1 и x2 соответствует один y)

Определение: Областью определения функции y = f(x) называется множество D(y) всех допустимых значений аргумента функции (то есть, множество всех значений независимой переменной, при которых функция определена).

Определение: Множеством (областью) значений функции y = f(x) называется множество E(y) всех значений, которые может принимать зависимая переменная.

Пример 1.

.

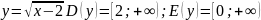Пример 2.

.

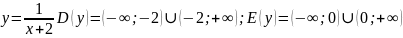Пример 3.

.

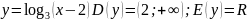Пример 4.

.

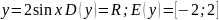Пример 5.

.

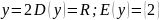. Нули функции. Промежутки знакопостоянства функции.

Определение: Нули функции – это значения независимой переменной, при которых функция принимает значение нуль.

Определение: Промежутки знакопостоянства функции – это промежутки из области определения функции, на каждом из которых функция принимает либо только положительные, либо только отрицательные значения (функция сохраняет знак).

Пример. Найти нули функции 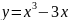и промежутки ее знакопостоянства.

1. 

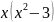=0

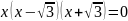
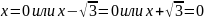
2. знаки функции y:

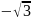
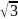
_ + _ + 0 x

Ответ: нули функции ;0; .

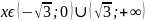y  0 при ; y  0 при .

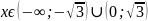. Четность функции.

Определение: Функция y = f(x) называется четной (нечетной), если для любого x из области определения выполняются два условия:

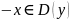1. (говорят, что область определения симметрична относительно нуля);

2. f(-x) = f(x) (f(-x) = - f(x))

Определение: Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида.

График четной функции симметричен относительно оси ординат (Оy); график нечетной функции симметричен относительно начала координат – точки (0;0).

Примеры:

Четные функции: ; .

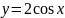Нечетные функции: ; ; .

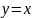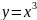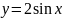Функции общего вида: ; .

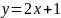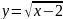Функция является и четной, и нечетной.

V. Периодичность функции.

Определение: Функция y = f(x) называется периодической, если существует число t  0, такое что для любого выполняются два условия:

1. ;

2. .

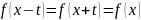Обычно работают с наименьшим положительным значением t, называя его основным периодом и обозначая через Т; Т  0.

График периодической функции состоит из повторяющихся с шагом Т фрагментов.

Примеры:

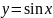– периодическая, t = 2n, n  Z\0, Т = 2;

– периодическая, t = n, n  Z\0, Т = ;

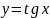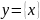– периодическая, t = n, n  Z\0, Т = 1 (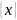 -дробная часть числа).

	2	y
	1								y=x
		0		1		2		3		4
-1												x