§ 3. Числовые множества.
. Множество натуральных чисел .
= 1; 2; 3; 4…
С помощью натуральных чисел (натура-природа (лат.)) люди считают предметы окружающего физического мира.
Очевидно, что множество замкнуто относительно операций сложения и умножения. Легко привести примеры (так называемые «контрпримеры»), которые опровергают замкнутость относительно операций вычитания и деления:
1) 1, 2, но 1 – 2; 2) 2, 4, но 2:4.
С последним обстоятельством связана неразрешимость на множестве даже такого простого уравнения как (1) a + x = b (a,b). Неразрешимость означает, что не для всех натуральных чисел a и b можно найти натуральное значение x такое, что уравнение (1) превратилось бы в верное числовое равенство.
Расширением множества является множество целых чисел, на котором уравнение вида (1) уже разрешимо (то есть имеет целое решение x = b – a при любых целых a и b).
. Множество целых чисел .
= …– 3; – 2; – 1; 0; 1; 2; 3; 4…
Множество целых чисел состоит из натуральных чисел, нуля и чисел, противоположных натуральным. Очевидно, что множество замкнуто относительно арифметических операций сложения, умножения и вычитания и незамкнуто относительно операции деления: 2 , 3 , но 2:3 .
Подчеркнем, что одного контрпримера достаточно, чтобы опровергнуть замкнутость (обосновать незамкнутость) множества.
Из
незамкнутости множества
относительно
операции деления следует, что уравнение
вида (2) ax
= b,
где a
,
b
неразрешимо на множестве .
Расширением множества целых чисел
является множество Q
рациональных чисел, на котором уравнение
вида (2) уже разрешимо
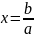(кроме
случая, когда a
= 0).
. Множество рациональных чисел Q.
Q
=
,
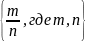то есть это множество всех дробей вида
,
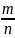где m
-
целое, n
-
натуральное.
Очевидно, что множество рациональных чисел замкнуто относительно всех четырех арифметических операций, кроме деления на нуль.
Для рациональных чисел справедливо следующее утверждение.
Всякое рациональное число можно представить (записать) в виде конечной или бесконечной периодической десятичной дроби. Верно и обратное утверждение.
Примеры:
- конечная десятичная дробь;
;
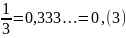– бесконечная периодическая дробь;
.
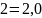Множество
рациональных чисел
обладает замечательным свойством: оно
всюду
плотно,
то есть между любыми двумя рациональными
числами существует бесконечно много
рациональных чисел. Поразительно, что,
несмотря на это, если на числовой оси
поставить все рациональные числа
(допустим, что это возможно), то на
числовой оси останется еще много
свободных мест. И эти места занимают
другие числа – иррациональные. ( В
середине
тысячелетия до нашей эры, предположительно,
в школе Пифагора была открыта
несоизмеримость отрезков: невозможно
выразить рациональным числом диагональ
квадрата со стороной, равной единице
(это будет бесконечная непериодическая
дробь
)
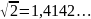Это открытие стало причиной первого
кризиса в математике, который был вскоре
преодолен).
V.
Множество
иррациональных чисел J(J
=
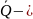дополнение
к множеству рациональных чисел Q).
Это множество всех бесконечных непериодических дробей.
Примеры:
;
;
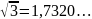Данное множество существенно отличается от всех предыдущих тем, что оно незамкнуто относительно всех арифметических операций. ( Убедитесь в этом, приведя соответствующие контрпримеры).
Заметим,
что уравнение вида (3)
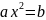(при
),
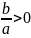неразрешимое на множестве Q,
на множестве иррациональных чисел имеет
два решения
и
,
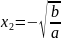то есть разрешимо.
Большую роль играют два иррациональных числа, обозначаемых буквами
= 3,1415926…3,14
e = 2,718281828…2,7
Числом («пи») называется отношение длины окружности к ее диаметру. С числом e вы познакомитесь чуть позже…
Объединением множеств рациональных и иррациональных чисел является множество действительных (вещественных) чисел.