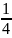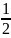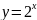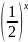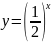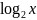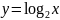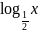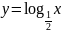- •Глава 1. Развитие понятия о числе.
- •§ 1. Основные операции над множествами.
- •§ 2. Замкнутость множеств.
- •§ 3. Числовые множества.
- •V. Множество действительных чисел r.
- •V. Множество комплексных чисел c.
- •Глава 2. Функции и их свойства.
- •§ 1. Понятие функции и её основные свойства.
- •V. Монотонность функции.
- •V. Стационарные и критические точки функции.
- •V. Точки экстремума и экстремумы функции.
- •V. Выпуклость и точки перегиба графика функции.
- •§ 2. Композиция функций и взаимно обратные функции.
- •Глава 3. Корни, степени и логарифмы.
- •§ 1. Корень натуральной степени и его свойства.
- •§ 2. Степень с действительным показателем.
- •§ 3. Иррациональные уравнения и неравенства.
- •§ 4. Логарифмы и их свойства.
- •§ 5. Показательная и логарифмическая функции, их графики и основные свойства.
- •§ 6. Показательные и логарифмические уравнения и неравенства.
§ 4. Логарифмы и их свойства.
. Понятие логарифма. Натуральный и десятичный логарифмы.
Определение. Логарифмом положительного числа b по положительному и не равному единице основанию a называется показатель степени, в который надо возвести число a, чтобы получить b.
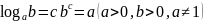
Из
определения непосредственно следует
равенство
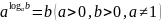 ,
называемое основным
логарифмическим тождеством.
,
называемое основным
логарифмическим тождеством.
Примеры:
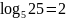 ,
так как
,
так как
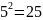 ;
;
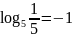 ;
;
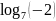 не определен, так как
не определен, так как
 ;
;
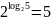 ;
;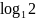 не определен, так как не выполнено
условие
не определен, так как не выполнено
условие
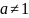 .
.
Для
удобства, ввиду частого использования,
логарифмы по основанию 10 назвали
десятичными
логарифмами, а логарифмы по основанию
е
- натуральными
логарифмами
и ввели следующие обозначения:
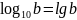 ;
;
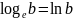 .
.
Примеры:
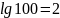 ,
так как
,
так как
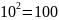 ;
;
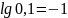 ,
так как
,
так как
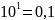 ;
;
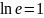 ,
так как
,
так как
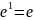 .
.
. Свойства логарифмов и основные формулы
Свойства логарифмов.
①
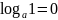 ;
②
;
②
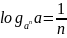 ;
;
③
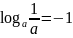 ;
④
;
④
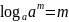 ;
;
⑤
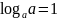 ;
⑥
;
⑥
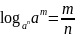 .
.
Основные формулы (соотношения):
①
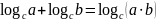 ;
;
②
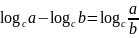 ;
;
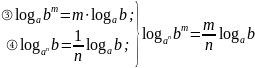
⑤ Формула перехода к новому основанию:
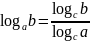 ;
в частности,
;
в частности,
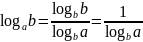 ;
;
Дополнительные формулы:
⑥
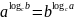 ;
;
⑦

Пример 1.
 ;
;
Пример 2.
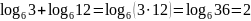 ;
;
Пример 3.
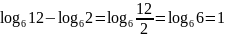 ;
;
Пример 4.
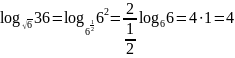 ;
;
Пример 5.
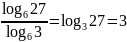 .
.
-
Вопросы и задачи
1 уровень
Вычислите:
а)
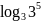 ;
б)
;
б)
 ;
в)
;
в)
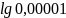 ;
г)
;
г)
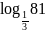 .
.
Вычислите:
а)
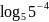 б)
б)
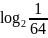 ;
в)
;
в)
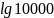 ;
г)
;
г)
 .
.
Вычислите:
а)
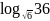 ;
б)
;
б)
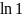 ;
в)
;
в)
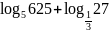 ;
г)
;
г)
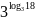 .
.
Вычислите:
а)
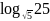 ;
б)
;
б)
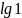 ;
в)
;
в)
 ;
г)
;
г)
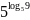 .
.
Выясните, при каких значениях x существует логарифм:
а)
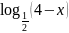 ;
б)
;
б)
 ;
в)
;
в)
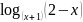 .
.
Выясните, при каких значениях x существует логарифм:
а)
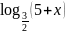 ;
б)
;
б)
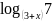 ;
в)
;
в)
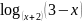 .
.
Вычислите:
а)
 ;
б)
;
б)
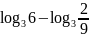 ;
в)
;
в)
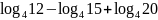 .
.
Вычислите:
а)
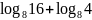 ;
б)
;
б)
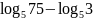 ;
в)
;
в)
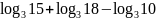 .
.
Вычислите:
а)
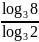 ;
б)
;
б)
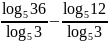 .
.
Вычислите:
а)
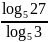 ;
б)
;
б)
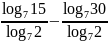 .
.
2 уровень
Вычислите:
а)
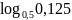 ;
б)
;
б)
 ;
в)
;
в)
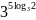 .
.
Вычислите:
а)
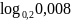 ;
б)
;
б)
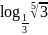 ;
в)
;
в)
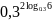 .
.
Вычислите:
а)
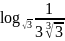 ;
б)
;
б)
 ;
в)
;
в)
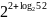 .
.
Вычислите:
а)
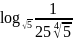 ;
б)
;
б)
 ;
в)
;
в)
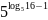 .
.
Выясните, при каких значениях x существует логарифм:
а)
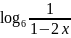 ;
б)
;
б)
 ;
в)
;
в)
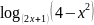 .
.
Выясните, при каких значениях x существует логарифм:
а)
 ;
б)
;
б)
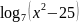 ;
в)
;
в)
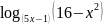 .
.
Вычислите:
а)
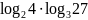 ;
б)
;
б)
 ;
в)
;
в)
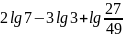 .
.
Вычислите:
а)
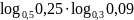 ;
б)
;
б)
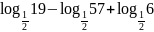 ;
в)
;
в)
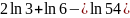 .
.
Вычислите:
а)
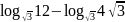 ;
б)
;
б)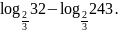
Вычислите:
а)
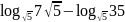 ;
б)
;
б)
 .
.
3 уровень
Вычислите:
а)
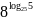 ;
б)
;
б)
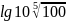 ;
в)
;
в)
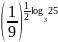 .
.
Вычислите:
а)
 ;
б)
;
б)
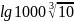 ;
в)
;
в)
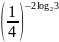 .
.
Вычислите:
а)
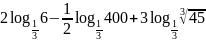 ;
б)
;
б)
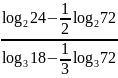 .
.
Вычислите:
а)
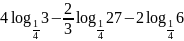 ;
б)
;
б)
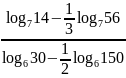 .
.
Выясните, при каких значениях x существует логарифм:
а)
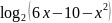 ;
б)
;
б)
 ;
в)
;
в)
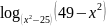 .
.
Выясните, при каких значениях x существует логарифм:
а)
 ;
б)
;
б)
 ;
в)
;
в)
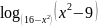 .
.
Вычислите:
а)
 ;
б)
;
б)
 ;
в)
;
в)
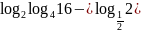 .
.
Вычислите:
а)
 ;
б)
;
б)
 ;
в)
;
в)
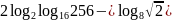 .
.
Вычислите:
а)
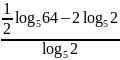 ;
б)
;
б)
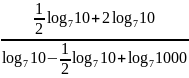 .
.
Вычислите:
а)
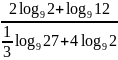 ;
б)
;
б)
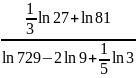 .
.
Вычислите:
а)
 ,
если
,
если
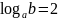 ;
;
б)
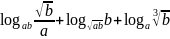 ,
если
.
,
если
.
Вычислите:
а)
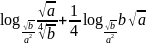 ,
если
,
если
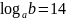 ;
;
б)
 ,
если
.
,
если
.
§ 5. Показательная и логарифмическая функции, их графики и основные свойства.
. Показательная функция, её свойства и график.
Определение:
Функция вида
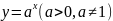 называется показательной.
называется показательной.
Основные свойства:
①
 ;
;
②
 ;
;
③ При
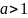 функция
функция
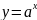 является возрастающей;
является возрастающей;
при
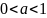 ,
функция является убывающей.
,
функция является убывающей.
График
показательной функции проходит через
точку (0;1),
так как
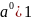 .
.
Для определенности пусть a = 2
|
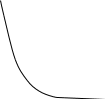
Для определенности пусть a = ½
|
. Логарифмическая функция, её свойства и график.
Определение:
Функция вида
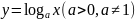 называется логарифмической.
называется логарифмической.
Основные свойства:
①
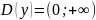 .
.
②
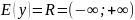 .
.
③ При
,
то функция
 является возрастающей; при
,
функция является убывающей.
является возрастающей; при
,
функция является убывающей.
График
логарифмической функции проходит через
точку (1;0), так как
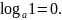
Для определенности пусть a = 2
|
Для определенности пусть a = ½
|
Замечание: показательная и логарифмическая функции с одинаковым основанием являются взаимно обратными, в связи с этим их графики симметричны относительно прямой y = x.
|
|
-
Вопросы и задачи
1 уровень
На координатной плоскости постройте графики функций:
а)
 ;
б)
;
б)
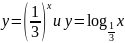 .
.
На координатной плоскости постройте графики функций:
а)
 ;
б)
;
б)
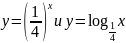 .
.
Найдите значение функции в точке x0:
а)
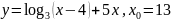 ;
б)
;
б)
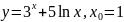 .
.
Найдите значение функции в точке x0:
а)
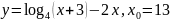 ;
б)
;
б)
 .
.
Укажите область определения функций:
а)
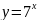 ;
б)
;
б)
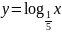 ;
в)
;
в)
 ;
г)
;
г)
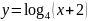 .
.
Укажите область определения функций:
а)
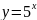 ;
б)
;
б)
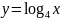 ;
в)
;
в)
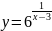 ;
г)
;
г)
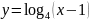 .
.
Укажите область значений функций:
а)
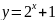 ;
б)
;
б)
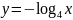 ;
в)
;
в)
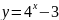 ;
г)
;
г)
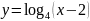 .
.
Укажите область значений функций:
а)
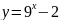 ;
б)
;
б)
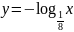 ;
в)
;
в)
 ;
г)
;
г)
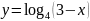 .
.
2 уровень
Укажите область определения функций:
а)
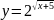 ;
б)
;
б)
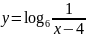 ;
в)
;
в)
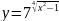 ;
г)
;
г)
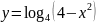 ;
д)
;
д)
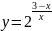 .
.
Укажите область определения функций:
а)
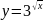 ;
б)
;
б)
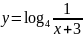 ;
в)
;
в)
 ;
г)
;
г)
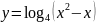 ;
д)
;
д)
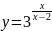 .
.
Укажите область значений функций:
а)
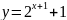 ;
б)
;
б)
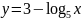 ;
в)
;
в)
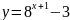 ;
г)
;
г)
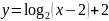 .
.
Укажите область значений функций:
а)
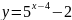 ;
б)
;
б)
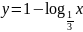 ;
в)
;
в)
 ;
г)
;
г)
 .
.
3 уровень
Найдите область определения функций:
а)
 ;
б)
;
б)
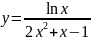 ;
в)
;
в)
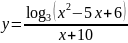 ;
г)
;
г)
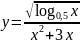 .
.
Найдите область определения функций:
а)
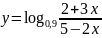 ;
б)
;
б)
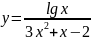 ;
в)
;
в)
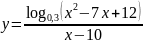 ;
г)
;
г)
 .
.
Найдите область значений функций:
а)
 ;
б)
;
б)
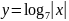 ;
в)
;
в)
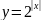 .
.
Найдите область значений функций:
а)
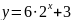 ;
б)
;
б)
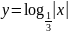 ;
в)
;
в)
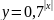 .
.
Постройте график функции и исследуйте её:
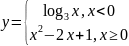 .
.Постройте график функции и исследуйте её:
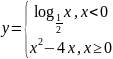 .
.Укажите горизонтальные и вертикальные асимптоты (если они есть) графиков функций:
а)
;
б)
 .
.
Укажите горизонтальные и вертикальные асимптоты (если они есть) графиков функций:
а)
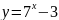 ;
б)
;
б)
 .
.
Найдите, обратную функцию для функций:
а)
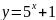 ;
б)
;
б)
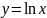 .
.
Найдите, обратную функцию для функций:
а)
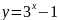 ;
б)
;
б)
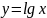 .
.