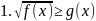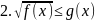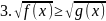- •Глава 1. Развитие понятия о числе.
- •§ 1. Основные операции над множествами.
- •§ 2. Замкнутость множеств.
- •§ 3. Числовые множества.
- •V. Множество действительных чисел r.
- •V. Множество комплексных чисел c.
- •Глава 2. Функции и их свойства.
- •§ 1. Понятие функции и её основные свойства.
- •V. Монотонность функции.
- •V. Стационарные и критические точки функции.
- •V. Точки экстремума и экстремумы функции.
- •V. Выпуклость и точки перегиба графика функции.
- •§ 2. Композиция функций и взаимно обратные функции.
- •Глава 3. Корни, степени и логарифмы.
- •§ 1. Корень натуральной степени и его свойства.
- •§ 2. Степень с действительным показателем.
- •§ 3. Иррациональные уравнения и неравенства.
- •§ 4. Логарифмы и их свойства.
- •§ 5. Показательная и логарифмическая функции, их графики и основные свойства.
- •§ 6. Показательные и логарифмические уравнения и неравенства.
§ 2. Степень с действительным показателем.
. Степень с рациональным показателем.
Степень
с натуральным показателем
определяется следующим образом:
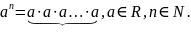
Примеры:
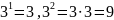 .
.
Степень с целым показателем доопределяется двумя следующими равенствами:
①
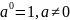 ;
;
②
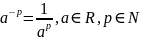 .
.
Примеры:
 .
.
Степень с рациональным показателем для неотрицательного числа a определяется так:
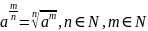 .
(при этом: если
.
(при этом: если
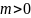 ,
то
,
то
 если
если
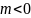 ,
то
,
то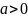 .)
.)
Примеры:
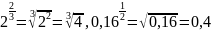 .
.
. Степень с действительным показателем.
Степень с иррациональным показателем строго не определяется, но, очевидно, что она существует.
Пример.

Таким
образом, можно говорить о степени
с действительным показателем
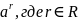 .
(если
.
(если
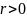 ,
то
,
то
 ,
если
,
если
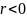 ,
то
).
,
то
).
Свойства степени:
①
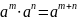 ;
;
②
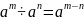 ;
;
③
 ;
;
④
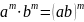 ;
;
⑤
 .
.
-
Вопросы и задачи
1 уровень
Представьте степень с дробным показателем в виде дроби:
а)
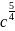 ;
б)
;
б)
 ;
в)
;
в)
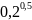 ;
г)
;
г)
 .
.
Представьте степень с дробным показателем в виде дроби:
а)
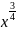 ;
б)
;
б)
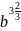 ;
в)
;
в)
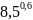 ;
г)
;
г)
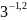 .
.
Представьте арифметический корень в виде степени с дробным показателем:
а)
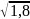 ;
б)
;
б)
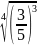 ;
в)
;
в)
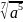 ;
г)
;
г)
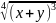 .
.
Представьте арифметический корень в виде степени с дробным показателем:
а)
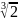 ;
б)
;
б)
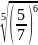 ;
в)
;
в)
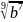 ;
г)
;
г)
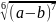 .
.
Найдите значение выражения:
а)
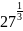 ;
б)
;
б)
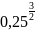 ;
в)
;
в)
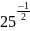 ;
г)
;
г)
 .
.
Найдите значение выражения:
а)
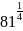 ;
б)
;
б)
 ;
в)
;
в)
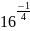 ;
г)
;
г)
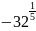 .
.
Представьте в виде степени с рациональным показателем:
а)
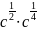 ;
б)
;
б)
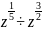 ;
в)
;
в)
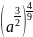 .
.
Представьте в виде степени с рациональным показателем:
а)
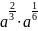 ;
б)
;
б)
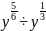 ;
в)
;
в)
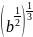 .
.
Найдите значение выражения:
а)
 ;
б)
;
б)
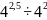 ;
в)
;
в)
 .
.
Найдите значение выражения:
а)
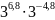 ;
б)
;
б)
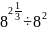 ;
в)
;
в)
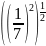 .
.
2 уровень
Представьте в виде степени с рациональным показателем:
а)
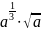 ;
б)
;
б)
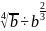 ;
в)
;
в)
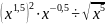 .
.
Представьте в виде степени с рациональным показателем:
а)
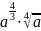 ;
б)
;
б)
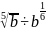 ;
в)
;
в)
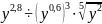 .
.
Вычислите:
а)
 ;
б)
;
б)
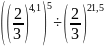 ;
в)
;
в)
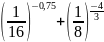 .
.
Вычислите:
а)
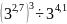 ;
б)
;
б)
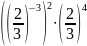 ;
в)
;
в)
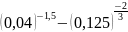 .
.
Вычислите:
а)
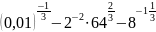 ;
б)
;
б)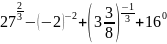 .
.
Вычислите:
а)
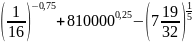 ;
б)
;
б)
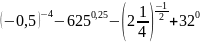 .
.
Упростите выражение:
а)
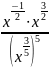 ;
б)
;
б)
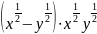 ;
в)
;
в)
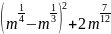 .
.
Упростите выражение:
а)
 ;
д)
;
д)
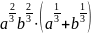 ;
б)
;
б)
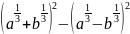 .
.
Сократите дробь:
а)
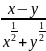 ;
б)
;
б)
 ;
в)
;
в)
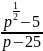 .
.
Сократите дробь:
а)
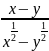 ;
б)
;
б)
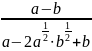 ;
в)
;
в)
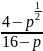 .
.
3 уровень
Вычислите:
а)
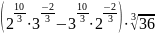 ;
б)
;
б)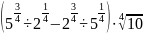 .
.
Вычислите:
а)
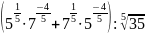 ;
б)
;
б)
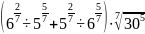 .
.
Упростите выражение:
а)
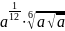 ;
б)
;
б)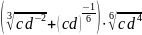 .
.
Упростите выражение:
а)
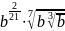 ;
б)
;
б)
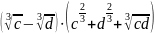 .
.
Упростите выражение:
а)
 ;
б)
;
б)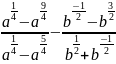 .
.
Упростите выражение:
а)
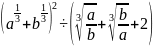 ;
б)
;
б)
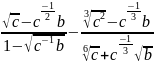 .
.
Упростите выражение:
а)
 ;
б)
;
б)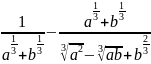 .
.
Упростите выражение:
а)
 ;
б)
;
б)
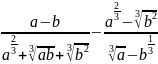 .
.
§ 3. Иррациональные уравнения и неравенства.
. Иррациональные уравнения.
Определение. Уравнения, в которых неизвестная величина находится под знаком радикала (корня) называются иррациональными.
Примеры:
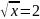 ;
;
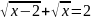 ;
;
 .
.
При решении иррациональных уравнений возможно расширение области допустимых значений уравнения (вследствие возведения в чётную степень), что может привести к появлению посторонних корней. Чтобы получить правильный ответ необходимо либо, найдя ОДЗ исходного уравнения, следить за равносильностью преобразований (добавляя ограничения в ОДЗ, если это потребуется), либо, найдя корни исходного уравнения, выполнить ПРОВЕРКУ, подставляя найденные корни в исходное уравнение.
Простейшие иррациональные уравнения имеют вид:
-
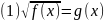
Уравнение (1) равносильно следующей системе:
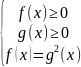
или
(2)
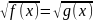
Уравнение (2) равносильно следующей системе:
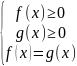
Очевидно, что одно из первых двух неравенств систем решать необязательно, так как оно следует из двух остальных.
Пример
1.
Решите уравнение:
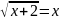 .
.
Возведём обе части уравнения в квадрат:
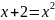 ;
;
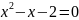 ;
;
x1 = 2, x2 = – 1.
Проверка:
1) x
=
2, тогда
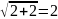 ,
,
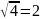 ,
2 = 2 – верно.
,
2 = 2 – верно.
2)
x
=
– 1, тогда
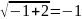 ,
1 = – 1 – неверно, то есть x
=
– 1 – посторонний корень.
,
1 = – 1 – неверно, то есть x
=
– 1 – посторонний корень.
Ответ: 2.
Решим пример 1 вторым способом (с ОДЗ)
.
ОДЗ:
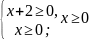
Возведя обе части в квадрат получим . Корень x = – 1 не входит в ОДЗ (не удовлетворяет условию x ≥ 0)
Ответ: 2.
Пример
2.
Решите уравнение:
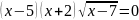 .
.
Исходное уравнение равносильно совокупности уравнений
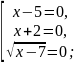

Учитывая ОДЗ: x – 7 ≥ 0, то есть x ≥ 7, необходимо отбросить посторонние корни 5 и – 2.
Ответ: 7.
Пример
3.
Решите уравнение
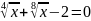 .
.
Введём
новую переменную
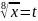 .
Получим уравнение
.
Получим уравнение
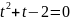 с корнями t1
=
1,
t2
=
– 2. Следовательно:
с корнями t1
=
1,
t2
=
– 2. Следовательно:
-
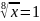
x = 1
или
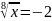
нет решений
Учитывая ОДЗ (x ≥ 0) или делая проверку, делаем вывод о том, что x = 1 является решением исходного уравнения.
Ответ: 1.
. Иррациональные неравенства.
Определение. Неравенства, в которых неизвестная величина находится под знаком радикала (корня), называются иррациональными.
Решение иррациональных неравенств, как правило, осуществляется путём возведения обеих частей неравенства в соответствующую степень. При этом необходимо следить за тем, чтобы при каждом преобразовании получалось неравенство, равносильное исходному. Это означает, что важную роль играет область допустимых значений неравенства.
Если обе части неравенства возводят в чётную степень, то полученное неравенство будет равносильно исходному только тогда, когда обе части исходного неравенства неотрицательны. При возведении обеих частей в нечётную степень всегда получается неравенство, равносильное исходному.
Таким образом, при решении иррациональных неравенств, нахождение ОДЗ и отслеживание равносильности преобразований обязательны (за редким исключением), так как ПРОВЕРКА, как правило, невозможна.
Простейшие иррациональные неравенства имеют вид:
|
|
|
Общие схемы решения следующие:

Данное неравенство равносильно совокупности систем неравенств:
 или
или
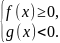
.
Данное неравенство равносильно совокупности систем неравенств (фактически, одной системе неравенств):
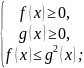 или
или
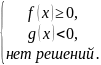
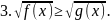
Данное неравенство равносильно следующей системе неравенств:
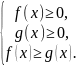
Пример
1.
Решите неравенство:
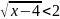 .
.
ОДЗ: x – 4 ≥ 0, то есть x ≥ 4. Обе части исходного неравенства неотрицательны, следовательно, можно возводить обе части неравенства в квадрат: x – 4 < 4; x < 8.
Учитывая
ОДЗ, имеем
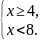 4 ≤ x
<8.
4 ≤ x
<8.
Ответ: [4; 8).
Пример
2.
Решите неравенство:
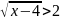 .
.
ОДЗ: x – 4 ≥ 0, то есть x ≥ 4. После возведения в квадрат: x – 4 > 4; x > 8.
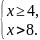 x
> 8.
x
> 8.
Ответ: (8; +∞).
Пример
3.
Решите неравенство:
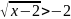 .
.
ОДЗ: x ≥ 2. Так как правая часть исходного неравенства отрицательна, то неравенство верно при всех допустимых значениях x.
Ответ: [2; +∞).
Пример
4.
Решите неравенство:
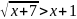 .
.
Решение оформляем по изложенной выше схеме:
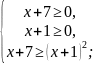 или
или
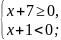
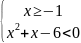 или
или
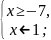
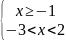 или
- 7 ≤ x
< –1.
или
- 7 ≤ x
< –1.
Ответ: [–7; 2).
-
Вопросы и задачи
1 уровень
Решите уравнения:
а)
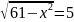 ;
б)
;
б)
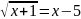 ;
в)
;
в)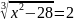 .
.
Решите уравнения:
а)
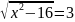 ;
б)
;
б)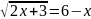 ;
в)
;
в)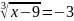 .
.
Решите уравнения:
а)
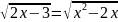 ;
б)
;
б)
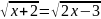 ;
в)
;
в)
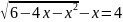 .
.
Решите уравнения:
а)
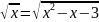 ;
б)
;
б)
 ;
в)
;
в)
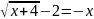 .
.
2 уровень
Решите уравнения:
а)
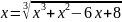 ;
б)
;
б)
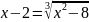 ;
в)
;
в)
 .
.
Решите уравнения:
а)
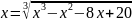 ;
б)
;
б)
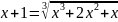 ;
в)
;
в)
 .
.
Решите неравенства:
а)
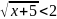 ;
б)
;
б)
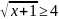 ;
в)
;
в)
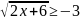 ;
г)
;
г)
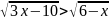 ;
д)
;
д)
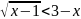 ;
е)
;
е)
 ;
ж)
;
ж)
 .
.
Решите неравенства:
а)
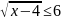 ;
б)
;
б)
 ;
в)
;
в)
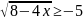 ;
г)
;
г)
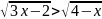 ;
д)
;
д)
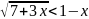 ;
е)
;
е)
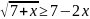 ;
ж)
;
ж)
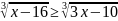 .
.
3 уровень
Решите уравнения:
а)
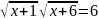 ;
б)
;
б)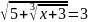 ;
в)
;
в)
 ;
г)
;
г)
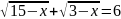 ;
д)
;
д)
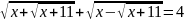 ;
е)
;
е)
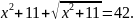
Решите уравнения:
а)
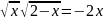 ;
б)
;
б)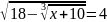 ;
в)
;
в)
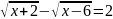 ;
г)
;
г)
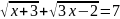 ;
д)
;
д)
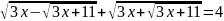 ;
е)
;
е)
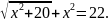
Найдите все значения параметра b, при которых уравнение
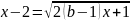 имеет единственное решение.
имеет единственное решение.Найдите все значения параметра p, при которых уравнение
 имеет единственное решение.
имеет единственное решение.Решите неравенства:
а)
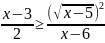 ;
б)
;
б)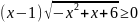 ;
в)
;
в)
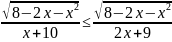 ;
;
г)
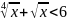 ;
д)
;
д)
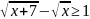 ;
е)
;
е)
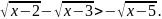
Решите неравенства:
а)
 ;
б)
;
б) ;
в)
;
в)
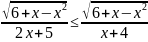 ;
г)
;
г)
 ;
д)
;
д)
 ;
е)
;
е)

Для каждого значения a решите неравенство
 .
.Для каждого значения a решите неравенство
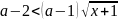 .
.