Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тихоокеанский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

statistika_3.docx

Скачиваний:

Добавлен:

01.07.2025

Размер:

63.99 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

Исходные данные

48	73	44	20	35	29	34	51	51	66
65	80	69	56	57	38	87	54	78	38
25	43	45	47	18	41	72	79	63	52
72	62	66	51	63	47	40	63	40	41
17	74	65	76	78	75	42	37	82	24
33	48	71	56	67	52	31	39	52	39
53	75	41	40	46	35	49	55	61	15
26	68	67	59	30	42	68	35	47	60
50	42	53	64	28	90	35	45	36	60
18	71	49	21	53	26	36	65	29	46




Построение интервального и дискретного вариационного ряда

Отсортируем имеющиеся данные по возрастанию

15	17	18	18	20	21	24	25	26	26
28	29	29	30	30	31	33	34	35	35
35	35	36	36	37	38	38	39	39	40
40	41	41	41	42	42	42	43	44	45
45	46	46	47	47	47	48	48	49	49
50	51	51	51	52	52	52	53	53	53
54	55	56	56	57	59	60	60	61	62
63	63	63	64	65	65	65	66	66	67
67	68	68	69	71	71	72	72	73	74
75	75	76	78	78	79	80	82	87	90

Построение интервального вариационного ряда.

Пусть x1, x2, x3… - совокупность значений случайной величины X, полученных в результате n независимых повторений некоторого эксперимента. Эта совокупность называется выборкой объёма n, а xi- выборочным значениями.

Элементы выборки, расположенные в порядке возрастания, образуют так называемый вариационный ряд. Пусть 1-число различных выборочных значений в данной выборке. Далее через 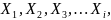будем обозначать только различные выборочные значения.

Вариационный ряд

X	15	17	18	20	21	24	25	26	28	29	30	31	33	34	35	36	37	38	39	40
частоты	1	1	2	1	1	1	1	2	1	2	2	1	1	1	4	2	1	2	2	2
X	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	59	60	61
частоты	3	3	1	1	2	2	3	2	2	1	3	3	3	1	1	2	1	1	2	1
X	62	63	64	65	66	67	68	69	71	72	73	74	75	76	78	79	80	82	87	90
частоты	1	3	1	3	2	2	2	1	2	2	1	1	2	1	2	1	1	1	1	1

Если случайная величина X дискретна и 1 велико или, если X непрерывна, то есть диапазон выборочных значений разбивают на k интервалов равной длины. Для определения оптимальной длины интервала можно использовать формулу Стерджеса:

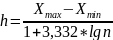
где X max, X min- соответственно максимальное и минимальное выборочное значение X. Если h окажется дробным, то за длину интервала надо взять либо ближайшее целое число, либо ближайшую, удобную для вычислений дробь. За начало первого интервала принимают величину 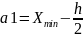. Если a₁-начало первого интервала, то a₂=a₁+h, a₃=a₂+h и т.д.

h= =9,786

Запишем интервальный и дискретный вариационные ряды. Дискретный ряд получим из интервального, заменив интервалы их серединами.

Интервалы		Сер. Интервалов	Частоты	Относительные частоты
10,11	19,89	15,00	4	0,04
19,89	29,68	24,79	9	0,09
29,68	39,47	34,57	16	0,16
39,47	49,25	44,36	21	0,21
49,25	59,04	54,14	16	0,16
59,04	68,82	63,93	17	0,17
68,82	78,61	73,72	12	0,12
78,61	88,40	83,50	4	0,04
88,40	98,18	93,29	1	0,01
			∑n=100	∑W=1

1 / 31 2 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.2025102.4 Кб2Shum_zash2.doc
#
15.05.20154.16 Mб24sp 23-101-2004.doc
#
01.05.202528.65 Кб1Spora.docx
#
21.11.20186.69 Mб51spravochnik_rtp_new.doc
#
01.05.20251.07 Mб1statistika.docx
#
01.07.202563.99 Кб0statistika_3.docx
#
01.07.202547.32 Кб3Statistika__Metod_ukazania__2.docx
#
15.05.2015762.57 Кб10stepanova_opredeliteli.pdf
#
22.09.2019993.79 Кб11stp_2_5_01_1_01.doc
#
18.03.201612.27 Mб32strateg_menedzh_fathutdinov.pdf
#
15.05.2015555.52 Кб26TEKhNIKA_SRT_KONEChNYJ_22_12_2013 (3).doc

48	73	44	20	35	29	34	51	51	66
65	80	69	56	57	38	87	54	78	38
25	43	45	47	18	41	72	79	63	52
72	62	66	51	63	47	40	63	40	41
17	74	65	76	78	75	42	37	82	24
33	48	71	56	67	52	31	39	52	39
53	75	41	40	46	35	49	55	61	15
26	68	67	59	30	42	68	35	47	60
50	42	53	64	28	90	35	45	36	60
18	71	49	21	53	26	36	65	29	46

15	17	18	18	20	21	24	25	26	26
28	29	29	30	30	31	33	34	35	35
35	35	36	36	37	38	38	39	39	40
40	41	41	41	42	42	42	43	44	45
45	46	46	47	47	47	48	48	49	49
50	51	51	51	52	52	52	53	53	53
54	55	56	56	57	59	60	60	61	62
63	63	63	64	65	65	65	66	66	67
67	68	68	69	71	71	72	72	73	74
75	75	76	78	78	79	80	82	87	90

48	73	44	20	35	29	34	51	51	66
65	80	69	56	57	38	87	54	78	38
25	43	45	47	18	41	72	79	63	52
72	62	66	51	63	47	40	63	40	41
17	74	65	76	78	75	42	37	82	24
33	48	71	56	67	52	31	39	52	39
53	75	41	40	46	35	49	55	61	15
26	68	67	59	30	42	68	35	47	60
50	42	53	64	28	90	35	45	36	60
18	71	49	21	53	26	36	65	29	46

15	17	18	18	20	21	24	25	26	26
28	29	29	30	30	31	33	34	35	35
35	35	36	36	37	38	38	39	39	40
40	41	41	41	42	42	42	43	44	45
45	46	46	47	47	47	48	48	49	49
50	51	51	51	52	52	52	53	53	53
54	55	56	56	57	59	60	60	61	62
63	63	63	64	65	65	65	66	66	67
67	68	68	69	71	71	72	72	73	74
75	75	76	78	78	79	80	82	87	90

48	73	44	20	35	29	34	51	51	66
65	80	69	56	57	38	87	54	78	38
25	43	45	47	18	41	72	79	63	52
72	62	66	51	63	47	40	63	40	41
17	74	65	76	78	75	42	37	82	24
33	48	71	56	67	52	31	39	52	39
53	75	41	40	46	35	49	55	61	15
26	68	67	59	30	42	68	35	47	60
50	42	53	64	28	90	35	45	36	60
18	71	49	21	53	26	36	65	29	46

15	17	18	18	20	21	24	25	26	26
28	29	29	30	30	31	33	34	35	35
35	35	36	36	37	38	38	39	39	40
40	41	41	41	42	42	42	43	44	45
45	46	46	47	47	47	48	48	49	49
50	51	51	51	52	52	52	53	53	53
54	55	56	56	57	59	60	60	61	62
63	63	63	64	65	65	65	66	66	67
67	68	68	69	71	71	72	72	73	74
75	75	76	78	78	79	80	82	87	90