
Решение:
а) По таблице истинности находим СДНФ и СКНФ
СДНФ:
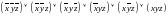
СКНФ:
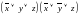
Минимизируем функцию с помощью карты Карно
Строим карту Карно

Интервалы области единиц:
{001,011,101,111}={--1}
{000,010}={0-0}
МДНФ:
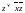
Интервалы области нулей:
{100,110}={1-0}
МКНФ:
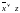
б) По таблице истинности находим СДНФ и СКНФ
СДНФ:

СКНФ:
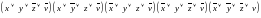
Минимизируем функцию с помощью карты Карно

Интервалы области единиц:
{0000,0001}={000-}
{0000,0100,1100,1000}={--00}
{0010,0110}={0-10}
{1000,1010}={10-0}
{1101,1111}={11-1}
{0111,1111}={-111}
МДНФ:
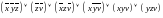
Интервалы области нулей:
{0011,1011}={-011}
{1001,1011}={10-1}
{0101}
{1110}
МКНФ:
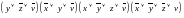
Задание №4
Булева
функция
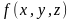 задана таблично. Показать, что система
из этой функции
задана таблично. Показать, что система
из этой функции
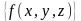 функционально полна, и выразить через
функцию
дизъюнкцию или конъюнкцию (на выбор).
функционально полна, и выразить через
функцию
дизъюнкцию или конъюнкцию (на выбор).
x |
y |
z |
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
|
|
5.6. |
Решение:
Для проверки на полноту системы, состоящей из этой функции, проверим функцию на принадлежность классам Поста:
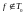 так
как
так
как
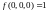
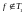 так
как
так
как
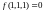
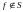 так
как
так
как
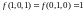
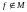 так
как
так
как
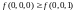
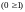
Чтобы проверить, принадлежит ли функция классу линейных функций, построим для неё полином Жегалкина:
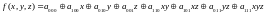
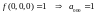
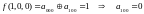
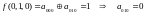
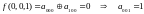
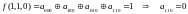
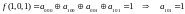
На
этом этапе уже видно что полином Жегалкина
содержит нелинейный член (xz),
таким образом
Поскольку функция не принадлежит ни одному из классов, то можно сделать вывод, что система из этой функции функционально полна
Задание №5
Можно ли с помощью указанных операций записать любую формулу алгебры высказываний?
6.6.
Дизъюнкция
и сложение по модулю 2
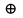 .
.
Решение:
Для
того чтобы ответить на данный вопрос,
выясним, полна ли функционально система
данных функций.
Построим
таблицу истинности для каждой функции
системы. При этом обозначим дизъюнкцию
как
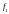 ,
а сложение по модулю 2 как
,
а сложение по модулю 2 как
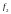 .
.
x |
y |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
x |
y |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
Исследуем на принадлежность классам Поста:
Сразу
видим, что
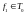 и
и
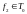 ,
так как
,
так как
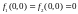 .
Следовательно система функций
не является функционально
полной, а это значит, что с помощью них
нельзя записать любую формулу алгебры
высказываний.
.
Следовательно система функций
не является функционально
полной, а это значит, что с помощью них
нельзя записать любую формулу алгебры
высказываний.
Заказать контрольную работу по дискретной математике и не только Вы можете у нас на сайте http://otl.su
Также посетите нашу группу Вконтакте: http://vk.com/otlsu
OTL.SU – Быстро, качественно, доступно!
