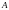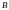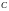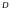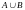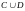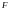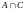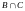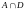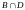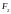Задание №1
Доказать равенство множеств:
а) исходя из определения равенства множеств;
б) Преобразуя левую (или правую) часть равенства в правую часть (соответственно, в левую);
в) используя характеристические функции и представляя множества с помощью булевых векторов.
1.6.
(A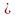 B)
(C
D)=(A
C)
(B
C)
(A
D)
(B
D)
B)
(C
D)=(A
C)
(B
C)
(A
D)
(B
D)
Решение:
а)
Пусть
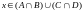 .
Тогда имеем: либо
.
Тогда имеем: либо
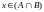 ,
либо
,
либо
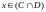 .
Если
,
то
.
Если
,
то
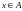 и
одновременно
и
одновременно
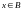 ,
если же
,
то
,
если же
,
то
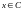 и одновременно
и одновременно
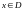 .
.
Предположим
что равенство верно. Тогда
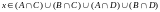 .
Это означает, что
.
Это означает, что
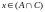 ,
либо
,
либо
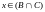 ,
либо
,
либо
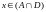 ,
либо
,
либо
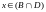 .
Значит x
одновременно
содержится либо в A
и
C,
либо,
B
и C,
либо A
и D,
либо B
и D.
Но исходя из первой части доказательства
этого не может быть (x
может одновременно содержаться либо в
A
и B,
либо в C
и D).
.
Значит x
одновременно
содержится либо в A
и
C,
либо,
B
и C,
либо A
и D,
либо B
и D.
Но исходя из первой части доказательства
этого не может быть (x
может одновременно содержаться либо в
A
и B,
либо в C
и D).
Таким образом, заключаем, что равенство неверно.
б) Преобразуем правую часть равенства, используя законы алгебры логики
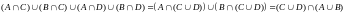
Следовательно, исходное равенство неверно, так как
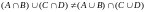
в) Построим таблицы истинности для правой и левой частей
Для левой части
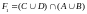
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Для правой части
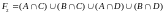
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
Как можно увидеть, последние столбцы в таблицах истинности не совпадают, следовательно, равенство неверно.