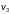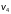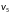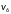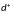Решение:

Составим матрицу смежности дополнительного графа

Для этого заменим в исходной матрице нули единицами, единицы нулями и получим матрицу смежности дополнительного графа

Задать и графически:

Граф :

Граф :

Запишем матрицы инцидентности для графов и :

Ребра соответствуют столбцам матрицы, а вершины графа строкам

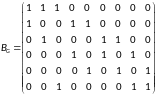
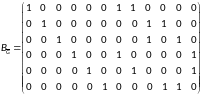
Рассчитаем степени вершин графов:

Учитываем, что при подсчете степени вершин, петля учитывается дважды.

	3	3	3	3	3	3
	4	4	4	4	4	4

Проверка изоморфности графов и :

Графы изоморфны, так как из матрицы смежности графа можно получить матрицу смежности графа , путем перестановок строк:

Поменяв местами во второй матрице первую строку с последней, а также 4-ю и 5-ю со 2-й и 3-й соответственно, получим первую матрицу.

Проверка связности графов:

Граф не является связным, так как, например, не существует цепи, которая соединяла бы вершины с номерами 6 и 4.

Граф является связным, так как для любой пары вершин найдется цепь, соединяющая их.

Пример цикла в графе и цепи, не являющейся циклом в графе :

Например, следующий цикл в графе не является циклом в графе :

Графы и оба являются планарными, потомучто их можно изобразить на плоскости без пересечения ребер, то есть:

Граф :

Граф :

Графы и оба не являются двудольными, потомучто в каждом из них содержится цикл нечетной длины:

Граф :

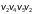
Граф :

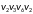
Графы и оба не являются эйлеровыми:

Граф : не является связным

Граф : все вершины имеют нечетную степень

Граф не является гамильтоновым, так как не является связным

Граф является гамильтоновым, так как существует простой цикл 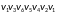который содержит все вершины графа ровно по одному разу.

Изобразим пример остовного ациклического подграфа графа :

Задача 11

Ориентированный граф задан матрицей смежности

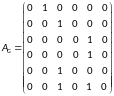
1) Задать графически

2) Рассчитать полустепени вершин

3) Составить матрицы инцинденстности и достижимости

4) Определить тип связности орграфа, выделить компоненты связности

Решение:

Зададим орграф графически

Рассчитаем полустепени вершин:

	1	1	1	1	1	2
	0	1	3	0	3	0

Составим матрицы инцинденстности и достижимости:

Обозначим дуги на нашем орграфе:

Строим матрицу инцидентности (столбцы соответствуют дугам, а строки вершинам)

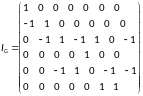
Находим матрицу достижимости :

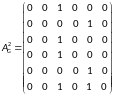
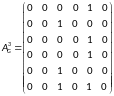
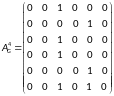
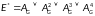
Таким образом, матрица достижимости имеет вид:

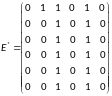
Определим тип связности орграфа:

Граф является слабо связным. Поскольку при учете направлений не каждая вершина оказывается достижима из любой, но при игнорировании направлений, получается связный граф.

Задача 12

Взвешенный граф задан матрицей весов. Построить его графическое представление, с помощью алгоритма Дейкстры определить матрицу расстояний. Найти радиус, центр и диаметр графа.

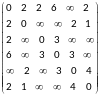
Изобразим данный граф:

Над каждым ребром подпишем его вес

Определим матрицу расстояний для данного графа:

	0	0+1=1	0+2=2	0+2+3=5	0+2+2=4	0+2=2
	0+2=2	0	0+2+2=4	0+2+3=5	0+2+3=5	0+1=1
	0+2=2	0+2+2=4	0	0+3=3	0+3+3=6	0+2+2=4
	0+3+2=5	0+3+2=5	0+3=3	0	0+3=3	0+3+2+1=6
	0+2+2=4	0+2+3=5	0+3+3=6	0+3=3	0	0+2+1=3
	0+2=2	0+1=1	0+2+2=4	0+3+2+1=6	0+2+1=3	0

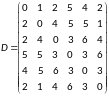
Определим для каждой вершины графа наибольшее удаление:

, , , , ,

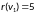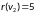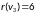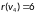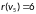Минимальное из полученных чисел является радиусом графа, а максимальное – диаметром:

,

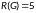Центрами являются вершины и

Заказать контрольную работу по дискретной математике и не только Вы можете у нас на сайте http://otl.su

Также посетите нашу группу Вконтакте: http://vk.com/otlsu

OTL.SU – Быстро, качественно, доступно!