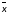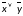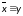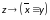Задача 1
Найти
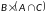 ,
,
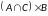 ,
,
 ,
если
,
если
 ,
,
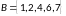 ,
,
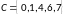
Решение:
Находим:
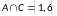

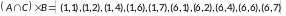
Очевидно,
что
 .
Тогда:
.
Тогда:
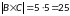
Задача 2
Найти область определения, область значений отношения
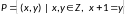
Является отношение рефлексивным, симметричным, антисимметричным, транзитивным?
Решение:
Найдем область определения:
Поскольку
 может принимать любые целочисленные
значения, то область определения будет
выглядеть так:
может принимать любые целочисленные
значения, то область определения будет
выглядеть так:

Найдем область значений:
Аналогично
и для
 .
Он тоже может принимать любые целочисленные
значения. Поэтому запишем область
значений:
.
Он тоже может принимать любые целочисленные
значения. Поэтому запишем область
значений:
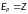
Отношение
не является
рефлексивным,
потому что
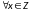
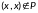 ,
то есть:
,
то есть:

Отношение
не является
симметричным,
потому что
 из того, что
из того, что
 не всегда следует что
не всегда следует что
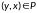 .
Например:
.
Например:
Пусть
 и
и
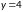 .
Тогда:
.
Тогда:
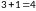 ,
но
,
но

Отношение является антисимметричным, потому что потому что из того, что всегда следует что . То есть:
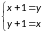
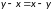
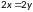
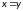
Отношение
не является
транзитивным,
потому что
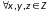 из того что
и одновременно
из того что
и одновременно
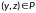 не следует что
.
Например:
не следует что
.
Например:
Пусть
,
и
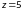 .
Тогда:
.
Тогда:
,
 ,
но
,
но

Задача 3
Сформулировать
высказывание, соответствующее формуле
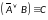
Решение:
A=”Невеста явилась в ЗАГС”
B=”Жених не явился в ЗАГС”
C=”Брак не состоялся”
Тогда:
 =”Невеста
не явилась в ЗАГС”
=”Невеста
не явилась в ЗАГС”
 =”Невеста
не явилась в ЗАГС ИЛИ жених не явился в
ЗАГС”
=”Невеста
не явилась в ЗАГС ИЛИ жених не явился в
ЗАГС”
То есть получаем следующее: «Брак не состоялся тогда и только тогда, когда невеста не явилась в ЗАГС или жених не явился в ЗАГС»
Задача 4
Найти
СДНФ и СКНФ формулы
 а) по таблице истинности, б) с помощью
эквивалентных преобразований. Составить
многочлен Жегалкина при помощи
эквивалентных преобразований исходной
формулы
а) по таблице истинности, б) с помощью
эквивалентных преобразований. Составить
многочлен Жегалкина при помощи
эквивалентных преобразований исходной
формулы
Решение:
Составим таблицу истинности для данной формулы:
|
|
|
|
|
|
|
|
f |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
Построим СДНФ по таблице истинности:
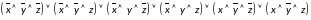
Построим СКНФ по таблице истинности:
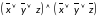
Составим полином Жегалкина, преобразовав исходную формулу:
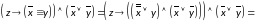


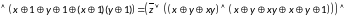

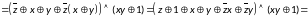
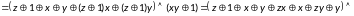

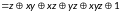
Задача 5
Минимизировать
в классе ДНФ логическую функцию
 ,
которая принимает значение 1 на следующих
наборах переменных (0, 5, 8, 9, 13)
,
которая принимает значение 1 на следующих
наборах переменных (0, 5, 8, 9, 13)