3. Метод приведения определителя к треугольному виду

С помощью элементарных преобразований определитель приводится к треугольному виду, когда все элементы, расположенные по одну сторону одной из диагоналей, равны нулю. Например, Значение определителя здесь вычисляется просто. Очевидно, что оно равно произведению элементов главной диагонали:

А = а₁₁  b₂₂  b₃₃  …  b_nn.

Однако, здесь следует помнить, что при перестановке строк (столбцов)знак определителя меняется на противоположный, а при умножении строки (столбца) на число на это число умножается весь определитель.

СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ

1. Определитель с нулевой строкой (столбцом) равен нулю.

2. Если какие-либо две строки (столбца) определителя пропорциональны, то он равен нулю.

3. Если какую-нибудь строку (столбец) определителя умножить на произвольное число, то и весь определитель умножится на это число.

4. Если какие-либо две строки (столбца) определителя поменять местами, то определитель изменит знак на противоположный.

5. Если к какой-нибудь строке (столбцу) определителя прибавить любую другую строку (столбец), умноженную на произвольное число, то определитель не изменится.

6. Определитель произведения матриц равен произведению их определителей.

Матрица, определитель которой равен нулю, называется вырожденной; матрица, определитель которой не равен нулю, называется невырожденной.

Контрольные вопросы:

1. Привести пример двух таких матриц, что определитель их суммы равен сумме их определителей. (Одна из матриц нулевая).

2. Может ли определитель 2-го порядка принимать значение большее, чем определитель 5-го порядка? (Да).

3. Как изменится определитель 3-го порядка, если его строки переставить следующим образом: первую – на место второй, вторую – на место третьей, третью – на место первой?

(Не изменится).

РАНГ МАТРИЦЫ

Минором k-го порядка матрицы А называется определитель, составленный из элементов матрицы, расположенных на пересечении каких-либо k строк и k столбцов.

Рангом матрицы А называется наибольший из порядков ее миноров, не равных нулю.

Обозначения: r ( A ), rang ( A ).

Базисным минором называется любой из миноров матрицы А, порядок которого равен r ( A ).

Метод элементарных преобразований нахождения ранга матрицы

При элементарных преобразованиях матрицы ее ранг не изменяется. Поэтому для нахождения ранга матрицы А ее с помощью элементарных преобразований нужно привести к ступенчатому виду. Количество ненулевых строк ступенчатой матрицы и есть искомый ранг матрицы А.

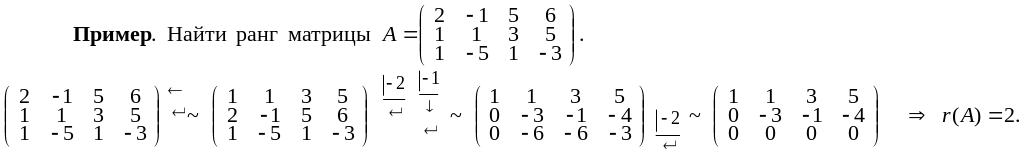
Задание для самоконтроля:

1. Найти ранги матриц А = и В = .

Метод окаймляющих миноров нахождения ранга матрицы

1) Найти какой-нибудь минор М₁ первого порядка (т.е. элемент матрицы), отличный от нуля. Если такого минора нет, то матрица А нулевая и r ( A ) = 0.

2. Вычислять миноры 2-го порядка, содержащие М₁ (окаймляющие М₁) до тех пор, пока не найдется минор М₂, отличный от нуля. Если такого минора нет, то r ( A ) = 1, если есть, то r ( A ) ≥ 2. И т.д.

  

k) Вычислять (если они существуют) миноры k-го порядка, окаймляющие минор

М _{k – 1} ≠ 0 до тех пор, пока не найдется минор М_k, отличный от нуля. Если такого минора нет, то r ( A ) = k –1, если есть, то r ( A ) ≥ k и процесс продолжается.

При нахождении ранга матрицы таким способом достаточно на каждом шагу найти всего один ненулевой минор k-го порядка, причем искать его только среди миноров

М _{k – 1} ≠ 0.

Пример.

Найти ранг матрицы методом окаймляющих миноров и указать один из базисных миноров: .

Т.к. у матрицы А есть ненулевые элементы, то r ( A ) ≥ 1. Найдем какой-либо ненулевой минор 2-го порядка (если он существует). Таким минором является, например, М₂ = = 3 ≠ 0. Значит, r ( A ) ≥ 2.

Вычислим миноры 3-го порядка, окаймляющие М₂: = = 0, = = 0.

Т.о., все миноры, окаймляющие М₂, равны нулю, следовательно, r ( A ) < 3. Итак, r ( A ) = 2.

Одним из базисных миноров является М₂ = .

Задание для самоконтроля:

Найти ранг матрицы методом окаймляющих миноров и указать один из базисных миноров:

1. . 2. .

Контрольные вопросы:

1. Может ли ранг матрицы быть равным нулю? меньше нуля? равным 2,5? (Да, нет, нет).

2. Ранг матрицы А равен r. Что можно сказать о r ( 2A )? r (–A )? r (0A )? (r, r, 0).

3. Как может измениться ранг матрицы при транспонировании? (Не изменяется).

4. Как может измениться ранг матрицы при добавлении к ней одной произвольной строки? одного произвольного столбца? (Может увеличиться на 1).

5. Как может измениться ранг матрицы при вычеркивании одной строки? одного столбца?

(Может уменьшиться на 1).