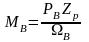Переходного теплового сопротивления на интервале 0 - 0,1 с

Из справочных данных [40] известно, что ударный ток, который выдерживает этот тиристор при температуре охлаждающего воздуха 40 ºС, является синусоидальным однополупериодным импульсом:

Как показывает результат расчёта кривой нагрева Т25 этим током (рис. 2.5), температура полупроводниковой структуры в момент закрывания вентиля и приложения обратного напряжения и восстановления его запирающих свойств оказывается 200 ºС. Указанный момент является наиболее опасным для полупроводниковой структуры, ввиду чего полученное значение температуры считается критериальным [35].

На рис. 2.6 представлен результат расчёта нагрева тиристора Т25 аварийным током короткого замыкания в трёхфазной мостовой схеме. Импульс рассматриваемого тока имеет среднее значение около 500 А. Анализ воспроизведённого аварийного режима показал, что в момент прекращения этого импульса температура полупроводниковой структуры меньше 200 ºС, т.е. ниже критериальной. Это означает, что тиристоры в данном случае выдержат перегрузку при условии срабатывания электронной защиты и снятия импульсов управления за время, меньшее 1/3 периода после достижения аварийным током амплитудного значения.

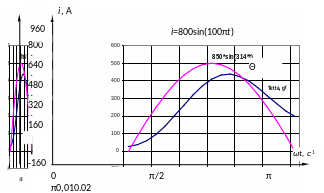
Рис. 2.5. График ударного тока Т25 и расчётная кривая нагрева

Θ

ωt, с^-1

π/3

2π/3

Рис. 2.6. Расчётные кривые тока короткого замыкания

И температуры нагрева тиристора т25

2.3. Математические модели машин переменного тока

2.3.1. Уравнения машины двойного питания

Машины переменного тока, в первую очередь асинхронные, составляют основной класс применяемых электродвигателей, а частотные электроприводы на их основе заняли лидирующее положение в регулируемом электроприводе. Важной задачей является освоение математического моделирования этих ответственных узлов современных автоматизированных систем.

При отображении функционирования машин переменного тока в составе регулируемого электропривода особое значение имеют точность и адекватность учёта электромеханического преобразования энергии и электромагнитного взаимодействие контуров статора и ротора в широком диапазоне частот вращения.

Рассматривается симметричная машина двойного питания с обмотками, соединёнными в звёзды (рис.2.19). Возможно подключение внешних цепей с источниками ЭДС, реактивными и пассивными элементами к зажимам А-В-С статора и a-b-c ротора

Рис.2.19. Схема обмоток машины переменного тока

Для упрощения идентификации моделей и облегчения расчётов целесообразно перейти к относительным единицам и выражать все переменные и параметры в долях от соответствующих базисных величин. Тогда относительные величины будут наглядно представлять степень загрузки и использования активных материалов, которая не меняется в столь широких пределах, как размеры и мощности машин.

Также запись расчётных соотношений в относительных единицах позволяет оперировать с безразмерными величинами в более узком диапазоне значений, что способствует повышению точности вычислений [49].

Амплитудные значения фазных напряжений и тока обмотки статора в номинальном режиме, а также угловой частоты напряжения питающей сети ω₁ и угла поворота результирующего вектора намагничивающей силы принимаются в качестве базисных, как это сделано в [49]

(2.20)

Производные базисные величины, выражаемые в соответствии с физическим смыслом через основные величины и с учётом числа Z_p пар полюсов на фазу, приведены в табл. 2.1.

Таблица 2.1. Производные базисные величины

Формула	Ед. изм	Название
	с	Время
	В·с	Потокосцепление
	Гн	Индуктивность
	Ф	Емкость
	Ом	Сопротивления
	Вт, В·А	Мощности
	Дж	Энергия
	рад	Угол поворота ротора
	с-1	Угловая частота вращения ротора
	кг∙м2	Момент инерции
	Н·м	Момент

Напряжения ветвей схемы (рис.2.19), соответствующих фазным обмоткам статора и ротора, выражаются в относительных единицах, согласно (2.8), по законам электромагнитной индукции и Ома для участка цепи

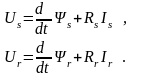(2.21)

В приведённых выражениях индекс s относится к напряжениям, потокосцеплениям токам и сопротивлениям статора, r – ротора. С применением метода контурных токов уравнения электрического равновесия фазных цепей статора и ротора (2.21) разрешаются относительно независимых потокосцеплений Ψ_AB, Ψ_ab, и токов I_AB, I_ab,

(2.22)

где , - линейные напряжения на зажимах обмоток,

значок «prime» ( ) означает транспонирование матрицы, прописные буквы в обозначениях фаз соответствуют цепям статора, а строчные – цепям ротора.

Уравнения (2.22) разрешаются к нормальному виду относительно производных потокосцеплений

(2.23)

При условии симметрии цепей, когда умножение векторов линейных напряжений на обратную матрицу 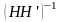означает переход к векторам напряжений фаз, выбранных в качестве независимых,

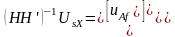
и выполняются соотношения

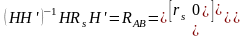
уравнение (2.23) оказывается разрешено относительно фазных величин

(2.24)

Потокосцепления и токи обмоток в (2.24) связаны через индуктивности намагничивающего контура и рассеяния (2.17). В общем случае они являются периодически изменяющимися величинами в зависимости от угла поворота ротора. Это вызывает сложности для представления процессов и дополнительные затраты времени на обращение матриц при интегрировании уравнений машины.

Обычной практикой является применение координатных преобразований физических величин, подробно описанных, например, в [46]. Благодаря этим преобразованиям, из рассмотрения исключаются периодические синусоидальные изменения физических величин и учитываются только изменения амплитудных и действующих значений. Рассмотрение физических величин на переменном токе переносится в область, аналогичную постоянному току, что существенно упрощает анализ хода протекания процесса и широко используется, в том числе, в системах векторного управления машинами переменного тока.

Координатные преобразования осуществляются на основе применения матриц поворота статора и ротора

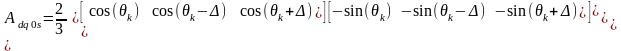(2.25)

где матрица A_dq0s применяется при третьем порядке векторов и матриц, или трёхфазном представлении, а матрица A_dqs – при двухфазном. Оба представления дают одинаковый результат, просто в трёхфазном варианте, чуть более громоздком и применяемом в дальнейшем изложении, естественным образом выполняются операции с векторами трёхфазных величин и матрицами параметров. У преобразованных трёхфазных величин третьи элементы полагаются нулевыми, что строго выполняется при симметрии цепей. Индекс ”dq” означает, что данная величина используется в преобразованном виде. Матрицы координатных преобразований для цепей ротора

(2.26)

Будем считать, что частота вращения системы координат ω_k совпадает с угловой частотой питающей сети ω₁, т.е. – угол поворота системы координат; Δ=2π/3. Отметим, что θ_r – угол поворота ротора относительно начального положения в переходном процессе не вычисляется непосредственно как функция времени ( ) и его нужно воспроизводить путём решения соответствующего уравнения состояния. Разница угловых частот вращения системы координат и ротора в относительных единицах представляет собой скольжение β=ω_k-ω_r.

Преобразованные величины выражаются через непреобразованные

(2.24)

где Е_dq01 и Е_dq02 представляют вектора преобразованных фазных ЭДС статора и ротора, т.е. источники энергии внешних цепей. Для обратного преобразования используются матрицы

, (2.25)

так что

(2.26)

После умножения уравнений (2.24) на матрицы поворота A_s и A_r и учёта обратных преобразований (2.26) получаются выражения для преобразованных напряжений обмоток статора и ротора

(2.27)

По правилу дифференцирования произведения имеем

(2.28)

Следует учесть соотношения, в которых получаются простейшие вещественные матрицы

(2.29)

Преобразованные напряжения статора и ротора согласно выведенным соотношениям

(2.30)

В уравнения (2.30), полученные для преобразованных величин, входят матрицы активных сопротивлений, которые в случае симметрии параметров обмоток не отличаются от исходных матриц, введённых при анализе непреобразованных величин

. (2.31)

Аналогично, с учётом (2.19) определяются матрицы индуктивностей рассеяния

. (2.32)

Приложение результатов анализа электромагнитных полей машины (2.13 – 2.19) к области преобразованных величин даёт следующие соотношения между потокосцеплениями и токами обмоток:

(2.33)

(2.34)

(2.35)

Дальнейший вывод зависит от того, какой конечный вид должна иметь модель, т.е. какие независимые переменные будут содержать итоговые уравнения. Обычно применяются следующие варианты описания электромагнитного взаимодействия обмоток статора и ротора: В настоящем варианте уравнения для преобразованных напряжений разрешаются относительно производных преобразованных токов статора и ротора

(2.36)

Определение величин U_dq0s и U_dq0r предусматривает учёт взаимосвязи цепей машины с внешними цепями. Вектора U_X, U_x линейных напряжений на зажимах статора и ротора выражаются с помощью топологической матрицы Н

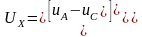. (2.37)

Они имеют второй порядок и, например, в простейшем случае, соответствующем применению асинхронного короткозамкнутого двигателя, подключённого к мощной сети, определяются с учётом принятых базисных величин как система синусоидальных напряжений и нулевой вектор:

. (2.38)

После координатных преобразований

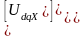(2.39)

дифференциальное уравнение, представляющее электромагнитное взаимодействие статора и ротора машины двойного питания, или уравнение состояния её цепей, принимает вид

(2.40)

г де

В (2.40) используются матрицы L_sr и R_sr индуктивного и активного взаимодействия контуров статора и ротора

.

В случае асинхронного короткозамкнутого двигателя вектор U_dxr преобразованных напряжений на зажимах ротора становится нулевым. Уравнению состояния (2.40) соответствует схема замещения (рис.2.20), содержащая взаимоиндуктивности, а внешние фазные ЭДС представляются элементами вектора U_X (2.39).

При использовании данной схемы для анализа процессов с учётом функционирования внешних устройств потребуется приравнивать напряжения на зажимах статора и ротора соответствующим напряжениям схем замещения этих устройств. При этом придётся либо осуществлять обратный переход от преобразованных величин машины к непреобразованным, либо применять преобразование параметров и переменных внешних схем замещения.

Рис. 2.20. Схема замещения машины переменного тока

Результирующий вектор преобразованных намагничивающих токов, определяемый по формуле

,

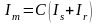не содержит компонент, не участвующих в формировании намагничивающих сил фазных обмоток вдоль дуги воздушного зазора. Направления векторов намагничивающих сил и главных потокосцеплений Ψ_m совпадают, их модули (нормы) связываются через индуктивность главного намагничивающего контура l_m. Величина этой индуктивности определяется по кривой намагничивания ψ_m(i_m). Так что можно учесть возможное насыщение магнитной цепи машины. Например, при аппроксимации кривой намагничивания гиперболическим синусом

_,

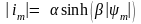где α и β – коэффициенты аппроксимации,

. (2.41)

Значения результирующих тока намагничивания и потокосцепления главного намагничивающего контура находятся через преобразованные токи намагничивания и потокосцепления намагничивания

. (2.42)

Электромагнитный момент, развиваемый электродвигателем, вычисляется по формуле

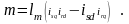(2.43)

Отображение электромеханического взаимодействия электродвигателя и нагрузки осуществляется на основе уравнений движения. Например, в случае неизменной статической нагрузки с моментом сопротивления m_c и моментом инерции j_m уравнения движения имеют вид

(2.44)

Таким образом, система уравнений (2.40) и (2.44) позволяет воспроизвести переходные процессы электромагнитного взаимодействия статора и ротора электрической машины переменного тока с возможным учётом подключения внешних цепей и электромеханического взаимодействия машины с нагрузкой.