1.2. Предметная область и классификация моделирования

Предметную область моделирования можно определить, исходя из общих представлений, как совокупность объектов и задач моделирования. Объектом моделирования автоматизированного электропривода может быть конкретное электротехническое устройство, часть устройства или комплекс устройств, процессы в которых интересуют исследователя. Для представления объектов и задач моделирования, рассматриваемых в настоящем пособии, на рис. 1.3 приведена в качестве примера упрощенная функциональная схема некоторого производственного участка.

Предполагается, что участок подключается к цеховой подстанции автоматическим выключателем QF, имеет мощный регулируемый электропривод постоянного тока (ТП-ДПТ) и ряд вспомогательных электроприводов (M1 – Mn). Микропроцессорная система управления (МПУ) обеспечивает взаимодействие всех элементов в соответствии с выполняемой производственной задачей. Функции локального управления отдельными узлами реализуются контактными и бесконтактными логическими схемами К1-Кn.

Рис. 1.3. Схема производственного участка

При разработке подобного комплекса электрооборудования с помощью математического моделирования могут быть выполнены различные задачи, например:

• оценка быстродействия системы ТП-ДПТ с переменным моментом инерции и нагрузки;

• анализ влияния процесса запуска мощного асинхронного двигателя (Mв) на работу системы электропривода постоянного тока;

• анализ нагрузок асинхронных двигателей (M1 – Mn) автоматической линии с целью выдачи рекомендаций по настройке защиты;

• оценка эффективности мероприятий по повышению производительности автоматической линии для заданного технологического процесса.

Задачу анализа автоматизированного электропривода упрощенно можно свести к получению зависимости вектора физических величин Y от векторов R и Х, представляющих параметры и внешние воздействия:

Y=f(R,X) .

Если набор R и Х детерминирован, т.е. задан как совокупность определённых значений, то анализ выполняется на основе одно- или многовариантного воспроизведения функционирования системы электропривода. Численные значения физических величин, полученные как функции времени, обрабатываются с целью определения характерных мгновенных или интегральных значений, представляющих технико-экономические показатели. Тогда результат получается в виде более или менее наглядной таблицы, а в идеальном случае – некоторого уравнения регрессии [9].

Также существует широкий класс задач, в которых значения параметров и внешних воздействий имеют в принципе случайную природу. Физическая величина здесь представляется в виде некоторой усреднённой функции с разбросом δy, т.е.

,

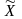где и - усреднённые значения параметров и внешних воздействий, а δR и δX – их разбросы.

Применительно к электроприводу можно выделить две основные группы подобных задач. В одной оцениваются надёжность, эффективность, энергопотребление, т.е. качество функционирования. В другой анализируются наличие очередей, простои, т.е. функционирование объектов с позиций теории массового обслуживания. Для решения задач анализа, связанных с воспроизведением факторов, формализованным по законам случайных событий, применяется имитационное моделирование [1]. Оно предусматривает отображение процесса функционирования объекта по некоторому алгоритму, функции блоков которого могут быть описаны различными способами, включая тексты, формулы, таблицы экспериментальных данных.

Для анализа объектов различной физической природы, размера и мощности применяются существенно различающиеся математические модели, что ставит задачу определения признаков их классификации. В соответствии с блочно-иерархическим принципом построения технических объектов естественным является разделение математических моделей по степени подчинённости. При этом можно отнести к отдельным уровням иерархии модели объектов, являющихся элементами, узлами, установками и системами в целом. Если принять эти уровни горизонтальными, то по вертикали становится возможным представить другие важные признаки моделей: рассматриваемые физические процессы, теоретические основы анализа и синтеза, применяемые численные методы, программные средства. Получается двумерная таблица, наглядно представляющая предметную область математического моделирования автоматизированного электрооборудования (табл. 1.1).

Можно утверждать, что для решения каждой конкретной задачи нужна специализированная модель с достаточной степенью детализации тех элементов и процессов, которые существенно влияют на результат анализа. Недопустимы как избыточные сложность и детализация модели, так и пренебрежение важными физическими особенностями объектов и задач. Здесь большое значение имеет квалификация постановщика задачи и ее исполнителя.

Таблица 1.1. Предметная область математического моделирования

Объекты	Процессы	Теория	Численные методы	Примеры программных средств
Элемент	Технологические Физико-химические Тепловые Электромагнитные	Математическая физика Термодинамика, Электродинамика	Экспертные оценки, диф. уравнения в частности производных	Специал. ППП Mathcad
Узел	Электромагнитные Электротепловые Электромеханические	ТОЭ, Теоретическая механика ТАУ Термодинамика	Диф. уравнения в частных производных, обыкновенные диф уравнения	Matlab P-cad Специал. ППП
Уста-новка	+ Информационные	+ Алгебра логики, теория автоматов	Обыкновеные. диф. уравнения Дискретные методы	Mathcad Matlab со Специал. библ.
Комп-лекс	+ Массового обслуживания	+ Теория вероят-ностей, теория оптимизации	Функционалы Множества	GPSS Специал. библ. Matlab

При решении вопросов практического применения моделей большое значение имеет уровень их проработки и развития. По аналогии с классификацией экспертных систем, приведённой в [19, с. 268], можно выделить: теоретическую модель, рабочую модель, промышленный и коммерческий прототипы. Для теоретической модели может быть предложено только математическое описание. Его полезность и работоспособность демонстрируются с помощью готовых программных средств. Это уровень постановки задачи на разработку модели с точки зрения стороннего заказчика.

Рабочая модель реализуется в виде программы, показывается ее достоверность и полезность. Это исследовательский прототип, который позволяет решать все поставленные практические задачи, но может эффективно функционировать только в руках разработчиков. Промышленный прототип, имеющий полный набор программной документации с описаниями применения и практическими примерами, может применяться квалифицированными заинтересованными заказчиками, для которых, собственно, модель и разрабатывается. Коммерческий прототип, имеющий удобные в применении текстовые и графические средства представления входных описаний исходных данных, процедур моделирования и обработки получаемых данных, а также средства диагностики и обучения, может быть передан сторонним пользователям.