
- •Модели оптимального развития энергосистем и сапр
- •Введение
- •1.3.2. Искусственные нейронные сети
- •Нормативно-балансовый метод
- •Метод экспертных оценок
- •Экстраполяционный метод
- •1. Технические показатели
- •2. Экономические показатели
- •2.7. Определение типа электростанции в условиях неопределенности
- •1. Выбор номинального напряжения электрической сети
- •2. Конфигурация
- •3. Выбор сечения
- •3.1. Организация проектирования энергетических систем
- •3.2. Назначение сапр
- •Библиографический список
- •Содержание
Нормативно-балансовый метод
Применяется при
планировании электропотребления на
основе планов производства различной
продукции
![]() в натуральных объемах для предприятий
- потребителей электроэнергии. При этом
используются нормируемые удельные
расходы электроэнергии
в натуральных объемах для предприятий
- потребителей электроэнергии. При этом
используются нормируемые удельные
расходы электроэнергии
![]() ,
измеряемые в кВт*ч
на единицу продукции. Прогнозируемый
объем необходимой электроэнергии:
,
измеряемые в кВт*ч
на единицу продукции. Прогнозируемый
объем необходимой электроэнергии:
![]() .
(1.12)
.
(1.12)
Удельные расходы электроэнергии приводятся в справочниках по проектированию энергосистем и систем электроснабжения. В качестве примера в таблице 1.9 приведены расходы по некоторым видам производства
Таблица 1.9
-
Наименование производства
Единица
продукции
Удельный расход,
кВт*ч
Добыча каменного угля закрытая
1 т угля
35-70
Добыча каменного угля открытая
То же
7-8
Добыча бурого угля закрытая
То же
10-15
Нефтедобыча насосным способом
1 т нефти
100-300
Доменное производство
1 т чугуна
10-13
Производство стали в дуговых печах
1 т
620-1135
Электролитное производство
1 т
3000-5000
Производство алюминия
1 т
10000-18400
Производство водорода
1 тыс. м3
5000-6000
Хлебозавод выпечка хлеба
1 т
70-80
Метод экспертных оценок
Используется для долгосрочного прогнозирования и в основном качественных показателей. Основан на учете и обработке мнений специалистов в своей предметной области. Существуют разные методы сбора экспертной информации:
индивидуальный, в основе которого интервью или подготовка пояснительной записки;
групповой метод (метод групповой экспертизы).
В групповом методе часто используется «мозговой штурм». При этом собранная группа специалистов свободно обменивается мнениями. В результате протоколируемой дискуссии появляются какие-то новые идеи, которые позже оцениваются уже другими специалистами. В результате возникают решения – традиционные и нетрадиционные. Иногда в такой экспертизе назначают повторную встречу, на которой обсуждаются результаты анализа и повторно решаются те же самые задачи (экспертиза с обратной связью по методу Делфи).
Экстраполяционный метод
Основан на сборе статистики, математическом анализе ее с целью определения устойчивых закономерностей, описываемых математическим выражением, и распространении их на будущее. При этом должно выполняться правило ретроспекции, по которому период прогнозирования не должен превышать одну треть периода ретроспекции (рис. 1.8).
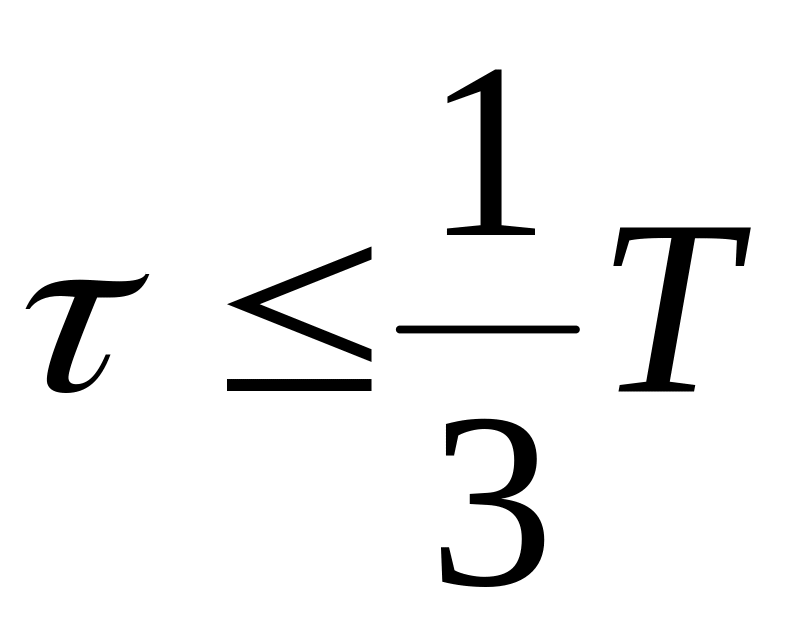 .
.

Рис. 1.8
В простейшем случае
в основе метода лежит обработка
статистической выборки, связывающей
каких-то два взаимосвязанных параметра
![]() и
и
![]() .
.
Итак, имеется
выборка
![]() ,
,
![]() ,
,
![]() ,…,
,…,![]() и выборка другого (прогнозируемого)
параметра
и выборка другого (прогнозируемого)
параметра
![]() ,
,
![]() ,
,
![]() ,…,
,…,![]() .
Задача заключается в определении
зависимости
.
Задача заключается в определении
зависимости
![]() ,
которая наилучшим образом описывает
статистические данные. Эту функцию
можно использовать для нахождения
промежуточных значений
при различных значениях
внутри этой таблицы
,
которая наилучшим образом описывает
статистические данные. Эту функцию
можно использовать для нахождения
промежуточных значений
при различных значениях
внутри этой таблицы
![]() ,
что называется интерполяцией,
а можно и за пределами таблицы
,
что называется интерполяцией,
а можно и за пределами таблицы
![]() ,
что называется экстраполяцией.
Часто за параметр
принимается время.
,
что называется экстраполяцией.
Часто за параметр
принимается время.
Обычно представляется многочленом -ого порядка, имеющим вид:
![]() .
(1.13)
.
(1.13)
Степень его заранее
не известна. Поэтому задача заключается
в определении в первую очередь порядка
многочлена. Для этого используют
табличные
разности,
которые определяют по исходной выборке,
имеющей постоянный шаг
![]() по
х,
полагая, что
по
х,
полагая, что
![]() .
Табличные разности определяются
следующим образом (табл. 1.10):
.
Табличные разности определяются
следующим образом (табл. 1.10):
Таблица 1.10
Определение табличных разностей
-
Разности I порядка
Разности II порядка
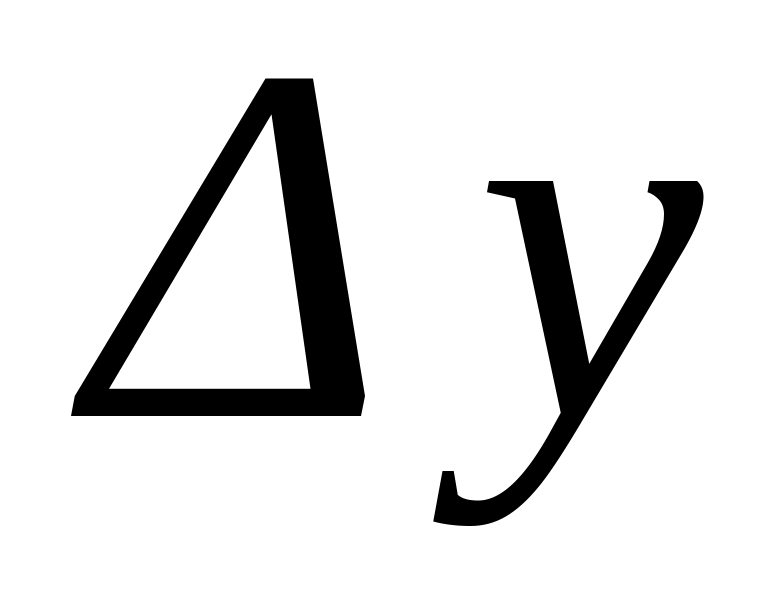
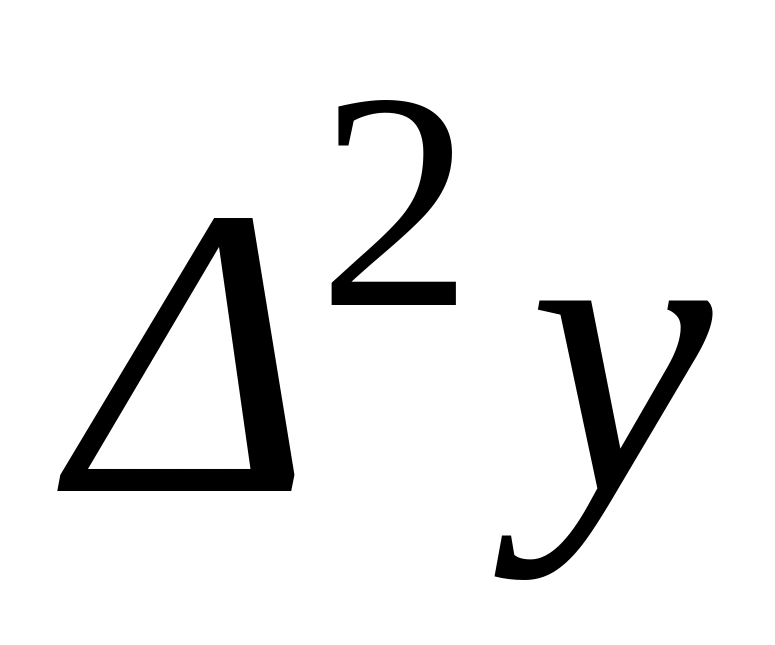
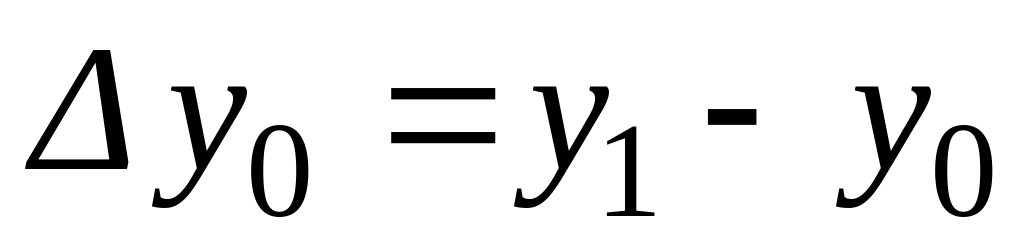
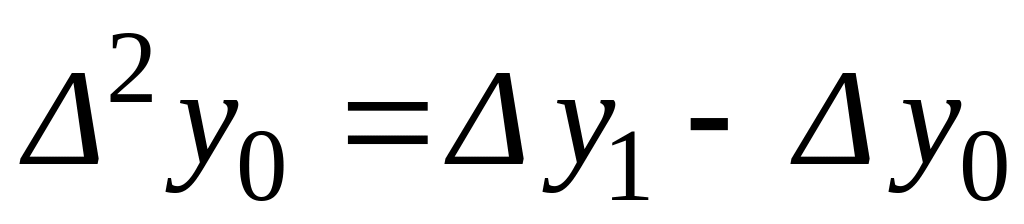



и т. д.
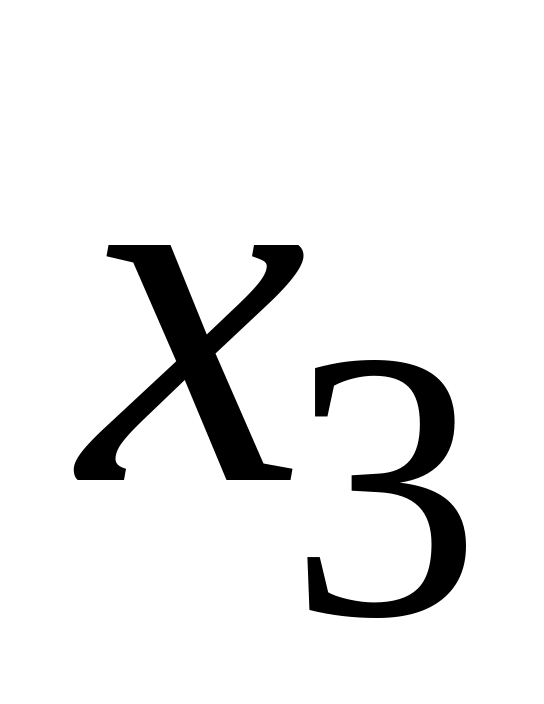
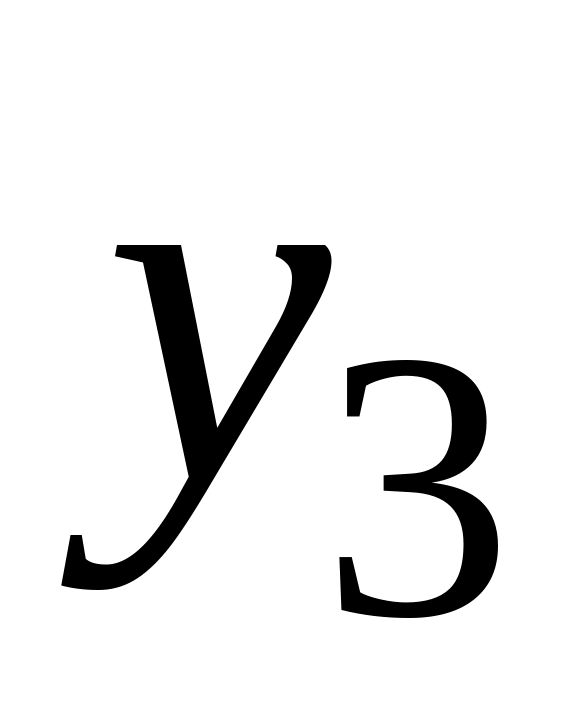
и т. д.
Как видно, табличные
разности
![]() -го
порядка определяются по следующему
правилу:
-го
порядка определяются по следующему
правилу:
![]() .
.
Оказывается, что
для многочлена
![]() -ого
порядка все табличные разности
-ого
порядка все табличные разности
![]() будут одинаковы, а
будут одинаковы, а
![]() .
.
Существует и
обратная связь: если при анализе табличных
разностей обнаружены одинаковые значения
для разностей
![]() ,
то статическая выборка хорошо описывается
многочленом
-ого
порядка. Определить ее можно, составив
по исходной выборке систему из
,
то статическая выборка хорошо описывается
многочленом
-ого
порядка. Определить ее можно, составив
по исходной выборке систему из
![]() уравнений:
уравнений:
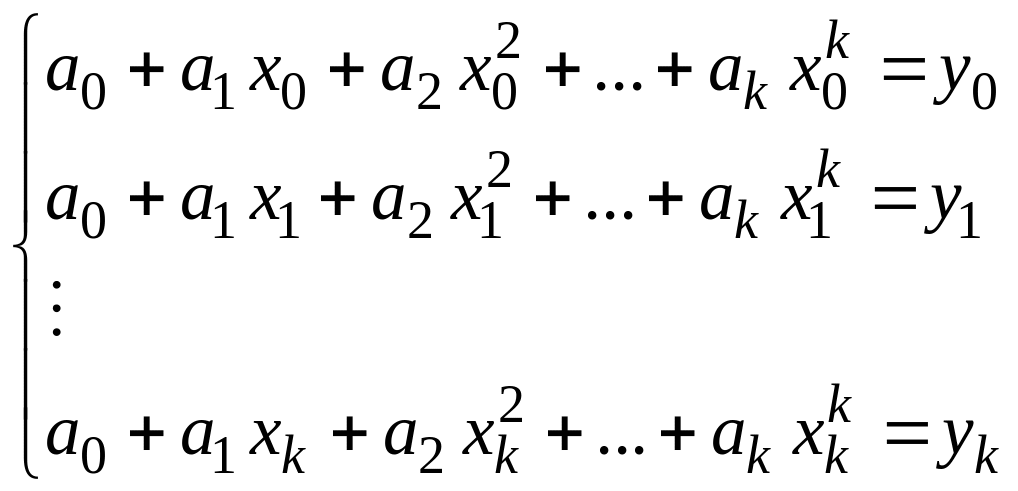 .
(1.14)
.
(1.14)
Решение этой
системы линейных алгебраических
уравнений позволяет найти все коэффициенты
от
![]() до
до
![]() .
.
Для определения
многочлена
![]() разработаны и другие методы, основанные
на применении полиномов, например, с
помощью полинома
Лагранжа:
разработаны и другие методы, основанные
на применении полиномов, например, с
помощью полинома
Лагранжа:
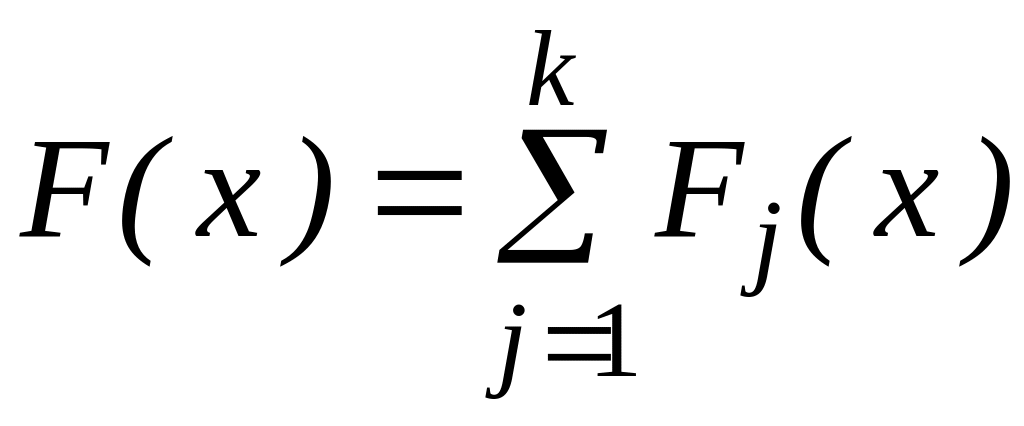 ,
(1.15)
,
(1.15)
в котором каждое слагаемое обладает следующим свойством
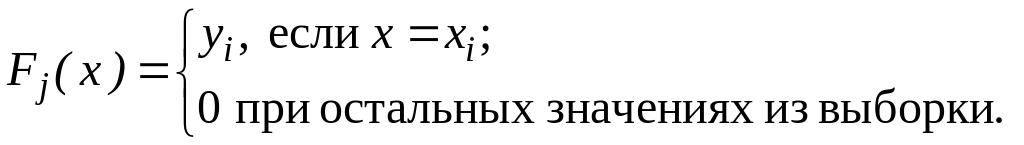
Каждое слагаемое формируется по формуле
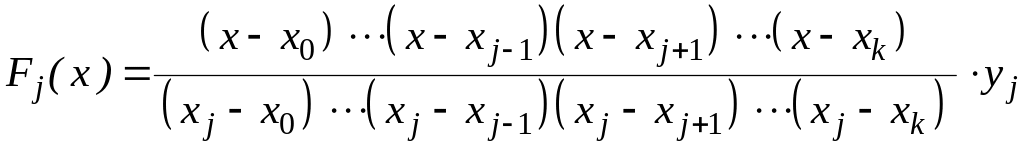 .
(1.16)
.
(1.16)
В рассмотренных методах используется не вся выборка, а только часть ее элементов, что не обеспечивает полного учета скрытых в выборке связей.
1.5. Метод наименьших квадратов
В этом методе для определения математического выражения используются все данные, описывающие выборку. При этом вид зависимости определяется в соответствии с характером процесса, оцениваемого по выборке. Функция, описывающая эту зависимость, называется предиктором или трентом. Наиболее простые и часто используемые предикторы:
![]() ,
,
![]() ,
,
![]() ,
,
![]() и др.
и др.
Неизвестные
коэффициенты
![]() для принятого предиктора подбираются
так, чтобы квадрат среднеквадратической
ошибки в точках выборки был минимальным.
В соответствии с этим формируется
целевая функция, зависящая только от
коэффициентов
для принятого предиктора подбираются
так, чтобы квадрат среднеквадратической
ошибки в точках выборки был минимальным.
В соответствии с этим формируется
целевая функция, зависящая только от
коэффициентов
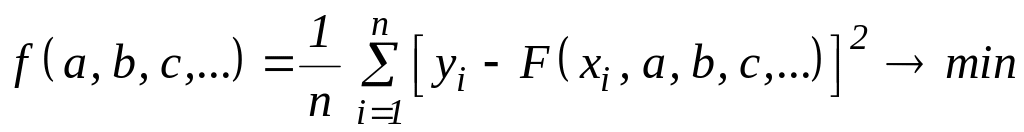 .
(1.17)
.
(1.17)
Чтобы найти
![]() ,
достаточно взять производные по
неизвестным коэффициентам:
,
достаточно взять производные по
неизвестным коэффициентам:
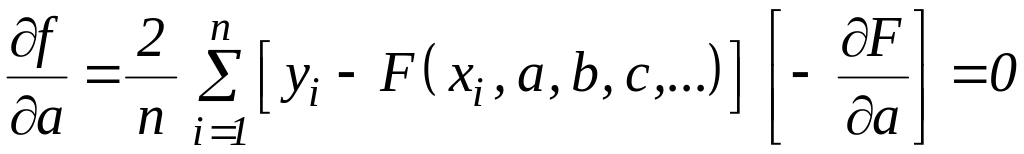 .
(1.18)
.
(1.18)
Значение «2» в числителе и знак «–» не существенны, поскольку правая часть равна 0. Аналогичные производные по остальным коэффициентам предиктора позволяют сформировать систему уравнений, решение которой и определяет все коэффициенты предиктора.
Рассмотрим все этапы определения коэффициентов линейного предиктора, для которого целевая функция:
 .
(1.19)
.
(1.19)
Производные по a и b образуют систему из 2-х уравнений
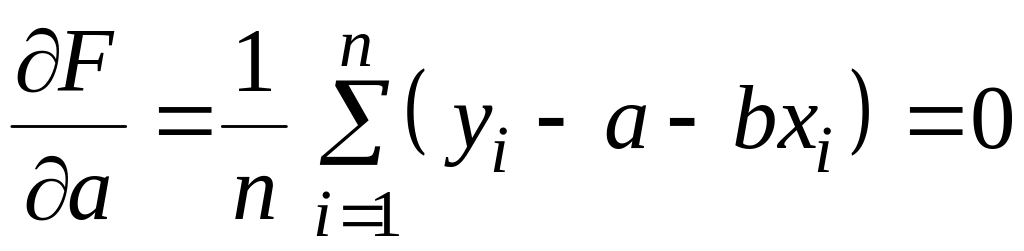 ,
(1.20)
,
(1.20)
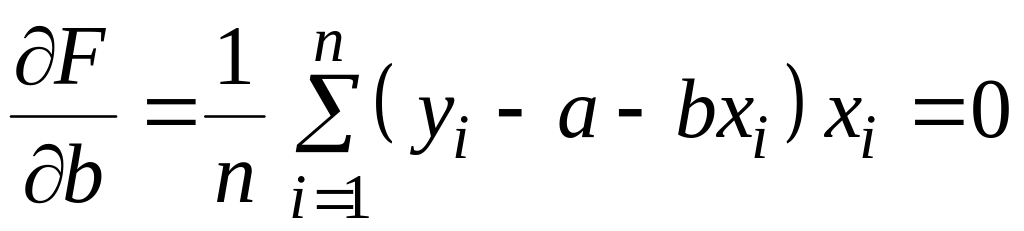 .
(1.21)
.
(1.21)
Введем следующие обозначения для средних значений:
 ;
;
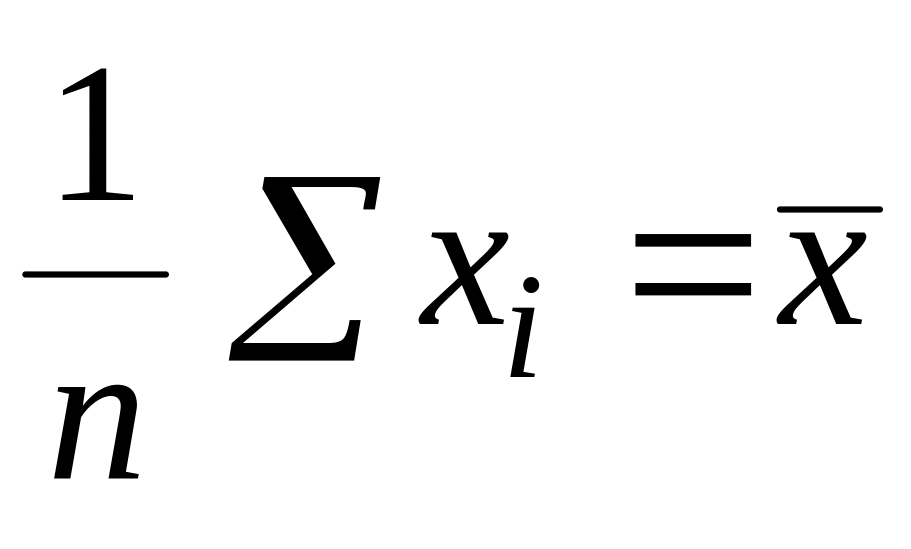 ;
;
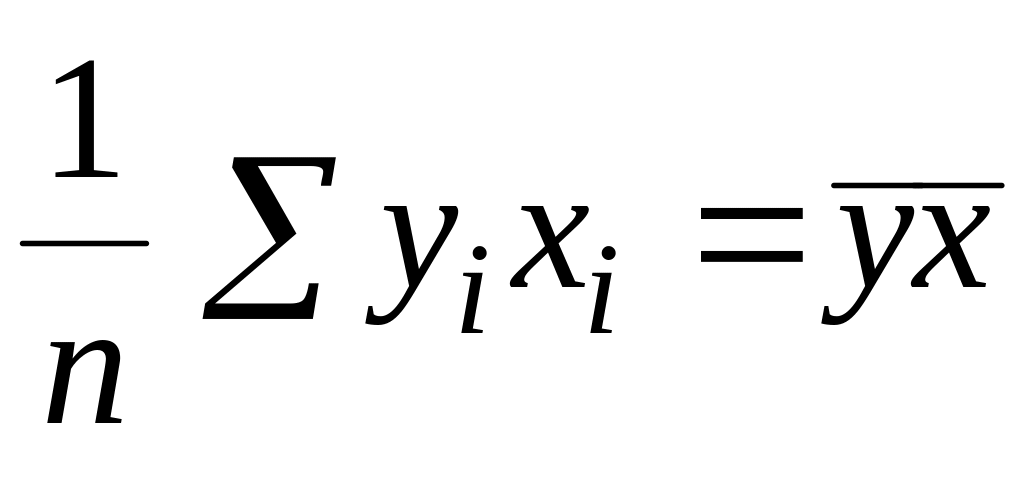 ;
;
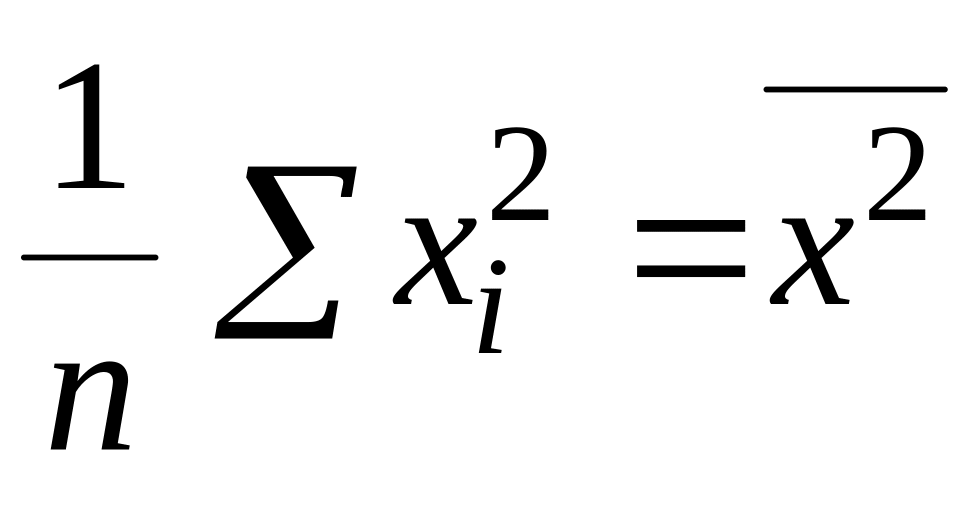 ,
,
с учетом которых система приводится к виду
 (1.22)
(1.22)
решение которой и определяет искомые коэффициенты
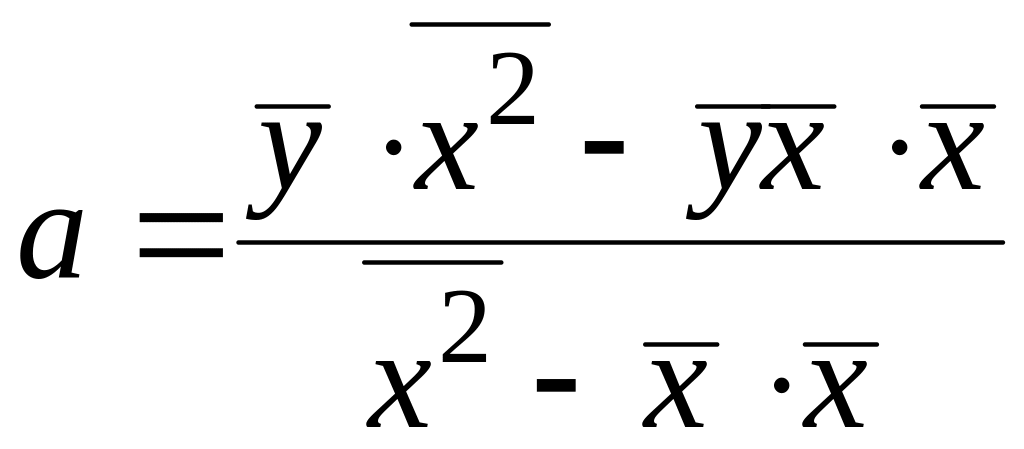 ;
;
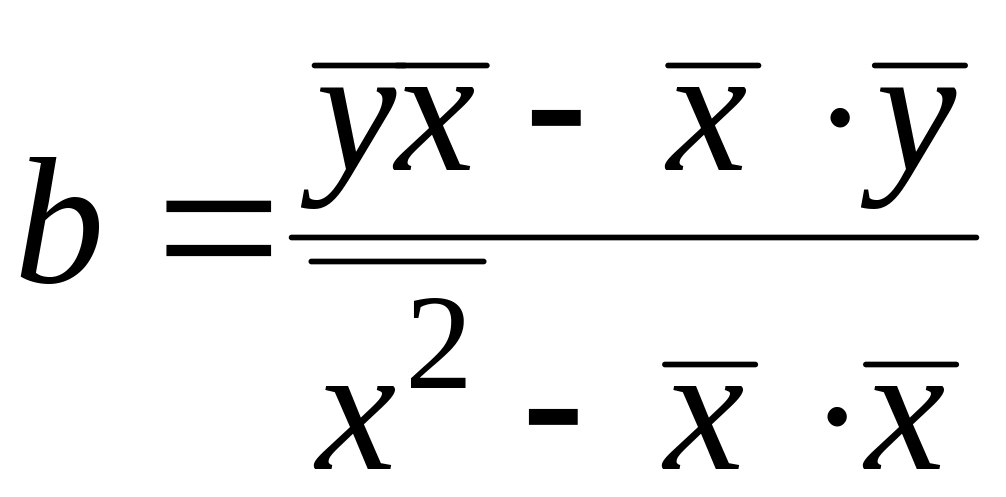 .
(1.23)
.
(1.23)
Для проверки
правильности выбора предиктора
используются различные критерии. Проще
всего определять допустимость предиктора,
сравнивая дисперсии сглаженной и
исходной выборки
![]() или путем анализа среднеквадратической
ошибки
или путем анализа среднеквадратической
ошибки
![]() .
.
Для предиктора СЛАУ формируется аналогично и имеет похожую структуру
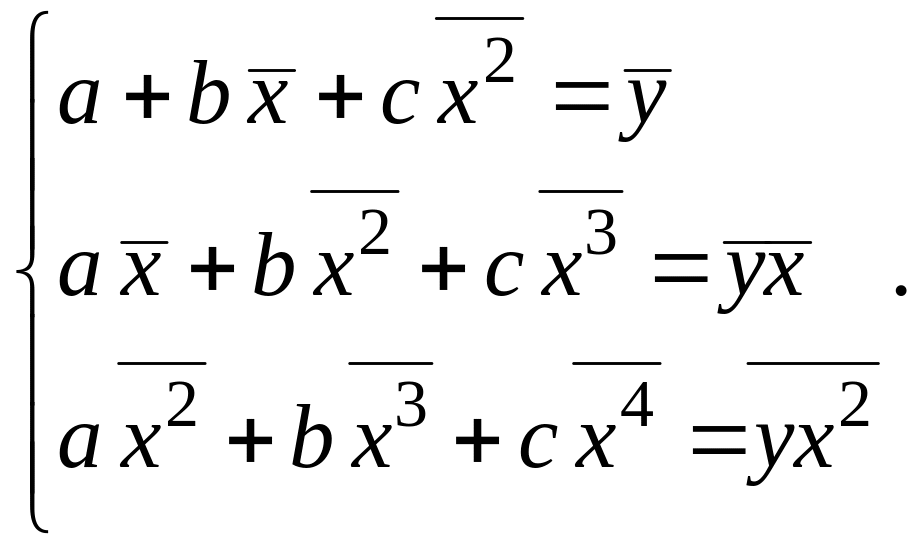 (1.24)
(1.24)
Как видно, матрица коэффициентов при неизвестных, определяемая значениями соответствующих средних, симметрична.
Часто на практике используют метод взвешенных наименьших квадратов, где каждый элемент выборки вводится в целевую функцию с определенным коэффициентом достоверности
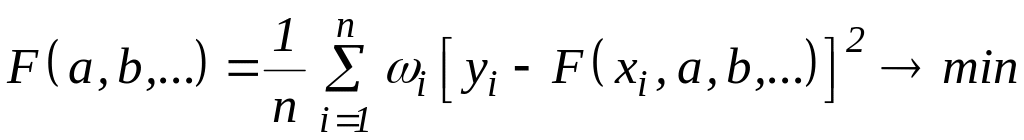 ,
(1.25)
,
(1.25)
где
![]() – коэффициент
достоверности.
– коэффициент
достоверности.
Пример 1.1.
Дана выборка, в которой представлены
мощность
![]() и электроэнергия
и электроэнергия
![]() .
.
Таблица 1.11
, МВт |
10,0 |
11,0 |
12,2 |
13,5 |
|
, ГВт·ч |
5,6 |
6,6 |
7,0 |
7,8 |
|
Определить ожидаемую мощность при пропуске электроэнергии 8,5 ГВт·ч.
Здесь – прогнозируемый параметр. Построим примерный вид зависимости по имеющейся информации.
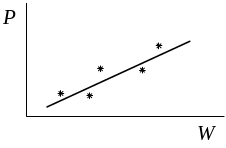
Рис. 1.9
Учитывая характер
зависимости, в качестве предиктора
выбираем
![]() .
Тогда
.
Тогда
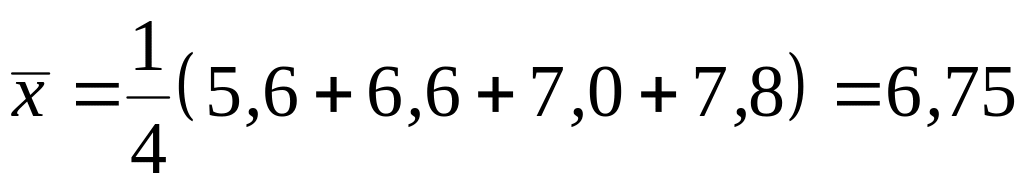 ;
;
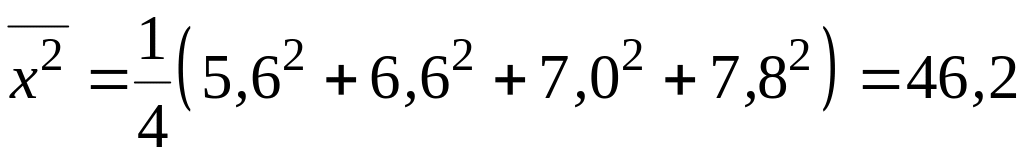 ;
;
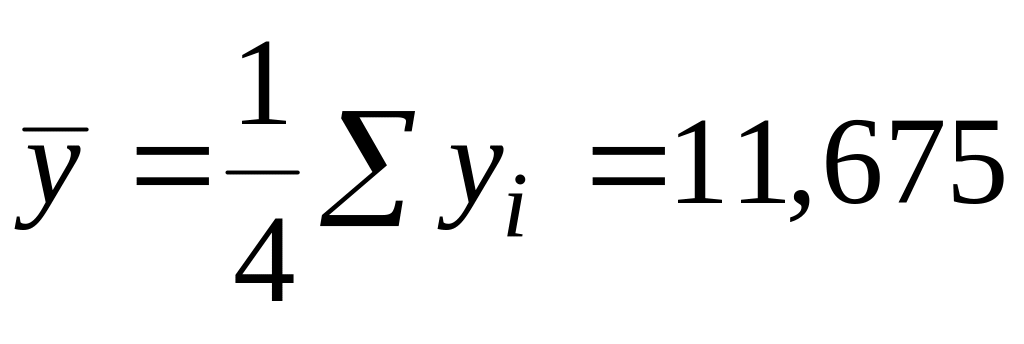 ;
;
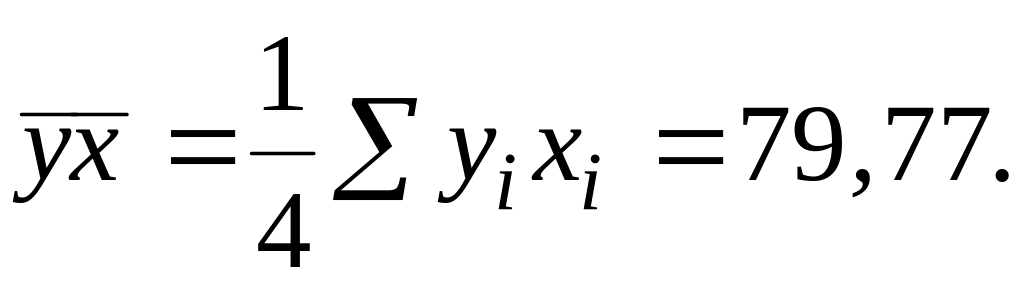 ..
..
Коэффициенты: 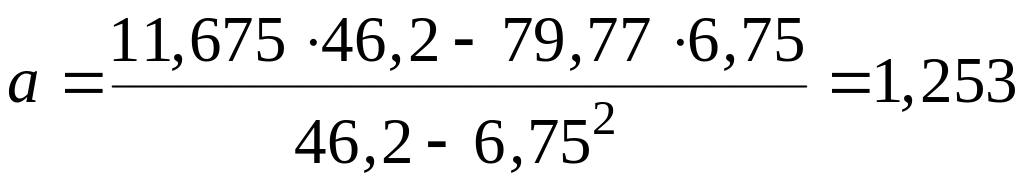 ;
;
 .
.
Таким образом, исходная выборка описывается выражением
![]() .
.
Проверим на достоверность выбранный предиктор. Определим ошибку сглаживания выборки в точках аппроксимации (табл. 1.12), среднеквадратическую ошибку и дисперсии:
Таблица 1.12
|
5,6 |
6,6 |
7,0 |
7,8 |
|
9,715 |
11,225 |
11,83 |
13,03 |
|
–0,285 |
0,225 |
–0,37 |
–0,47 |
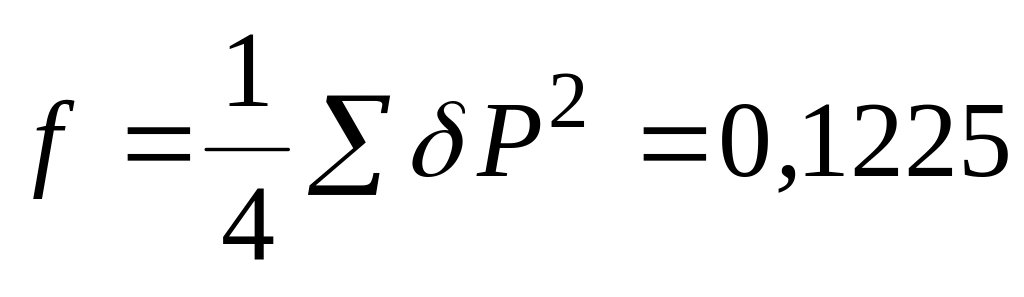 ;
;
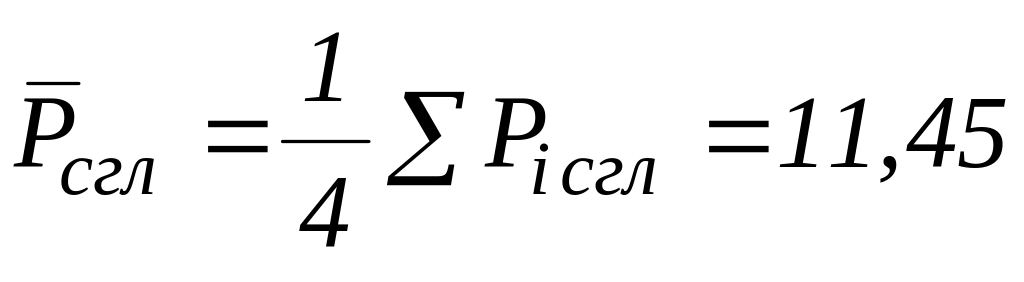 ;
;
![]() .
.
Далее определим дисперсии:
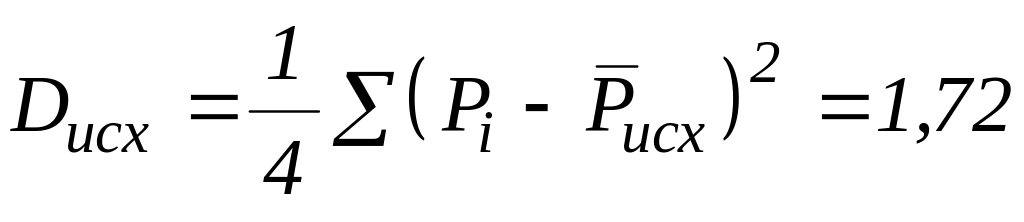 ;
;
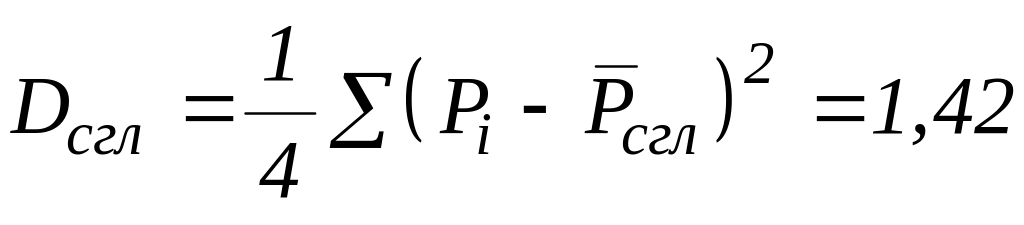 .
.
Таким образом, оба условия достоверности предиктора и выполняются, и полученное выражение можно использовать для прогноза. При =8,5 ожидаемое значение мощности
![]() .
.
При прогнозировании временных зависимостей, например, изменения электрических нагрузок, на общую закономерность, обычно линейную, называемую трендом, накладываются периодические и случайные составляющие. Соответствующий им статистический ряд можно определить как разность исходной выборки и найденной функции линейного предиктора. Полученную выборку можно аппроксимировать тригонометрическими функциями или гармоническим рядом Фурье с определением коэффициентов методом наименьших квадратов.
1.6. Корреляционный анализ
В больших системах действуют случайные процессы. Случайные параметры в системах взаимосвязаны. Например, погодные условия влияют на потребление электроэнергии, количество осадков влияет на выработку электроэнергии на ГЭС, и таких примеров в окружающем мире можно привести достаточно много. Взаимосвязь случайных процессов описывается уравнениями регрессии, которые могут использоваться для того, чтобы определить по одному или нескольким ожидаемым значениям случайных параметров математическое ожидание другого прогнозируемого параметра. При этом в первую очередь надо учитывать те параметры, которые наиболее сильно влияют на прогнозируемый.
Для оценки степени связи случайных процессов используется корреляционный анализ. Рассмотрим простейший процесс, который представлен выборкой для двух случайных параметров.
Таблица 1.13
|
|
|
… |
|
|
|
|
… |
|
Будем считать, что прогнозируемый параметр . Степень связи определяется коэффициентом корреляции. Для представительной выборки, являющейся результатом глубоких статистических наблюдений, коэффициенты парной корреляции определяются по следующей формуле:
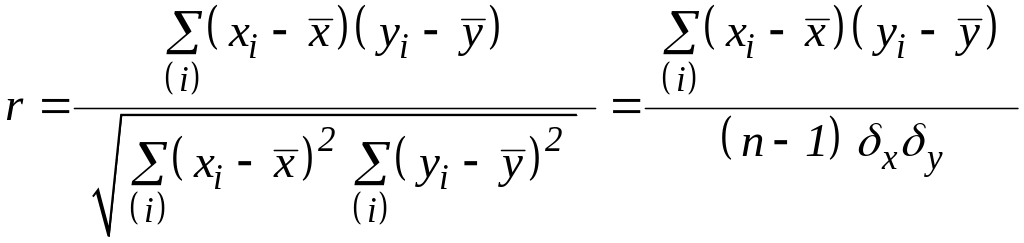 .
(1.26)
.
(1.26)
Здесь учтены
следующие соотношения для дисперсий
при больших выборках
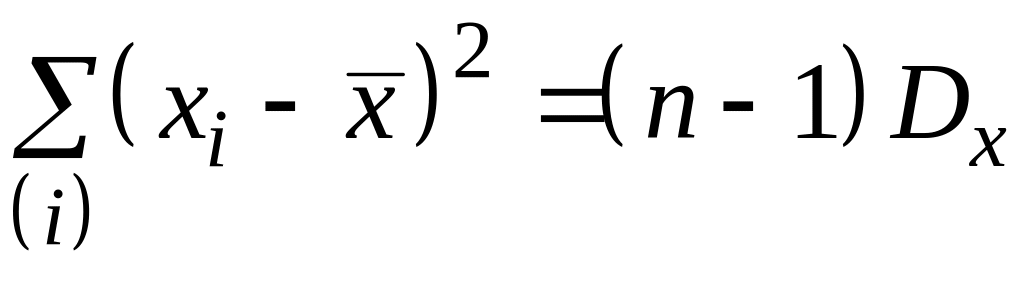 и
и
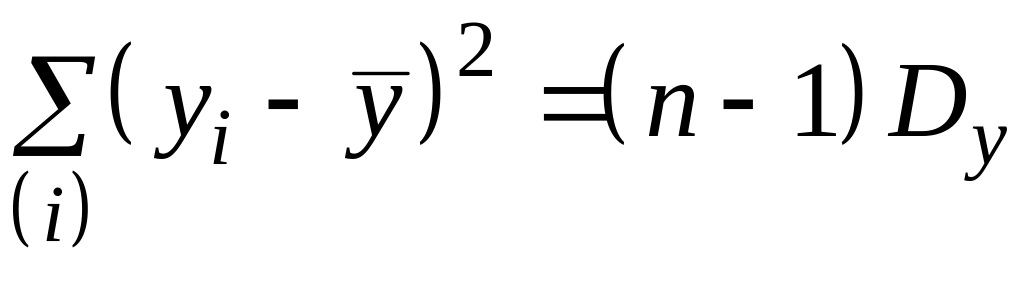 ,
а также стандартные отклонения
,
а также стандартные отклонения
![]() и
и
![]() .
.
Коэффициент
корреляции лежит в пределах
![]() ,
определяя при этом степень и характер
взаимосвязи параметров наблюдения:
,
определяя при этом степень и характер
взаимосвязи параметров наблюдения:
|
– случайные процессы совершенно не взаимосвязаны; |
|
– связь очень сильная; |
|
– связь прямо пропорциональная; |
|
– связь обратно пропорциональная. |
С использованием
коэффициента корреляции
![]() можно определить уравнения линейной
регрессии, позволяющие по ожидаемому
значению X
или Y
получить математическое ожидание
другого параметра:
можно определить уравнения линейной
регрессии, позволяющие по ожидаемому
значению X
или Y
получить математическое ожидание
другого параметра:
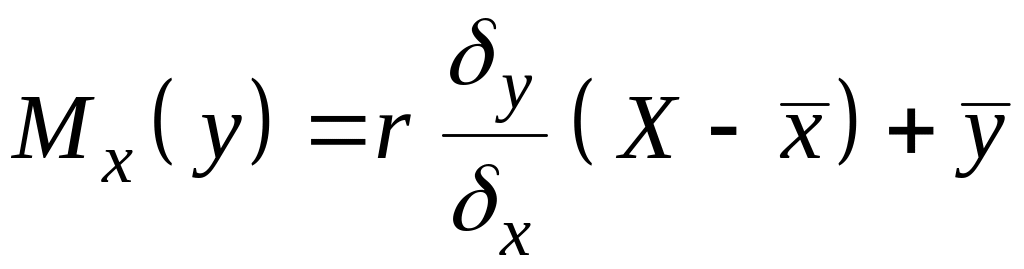 ;
(1.27)
;
(1.27)
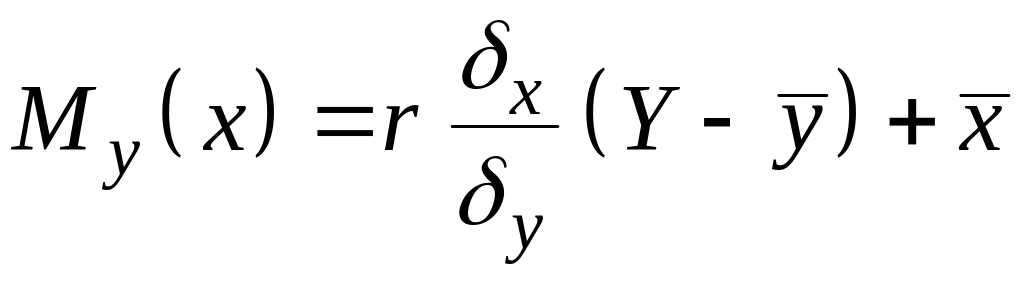 .
(1.28)
.
(1.28)
Здесь средние
 ;
;
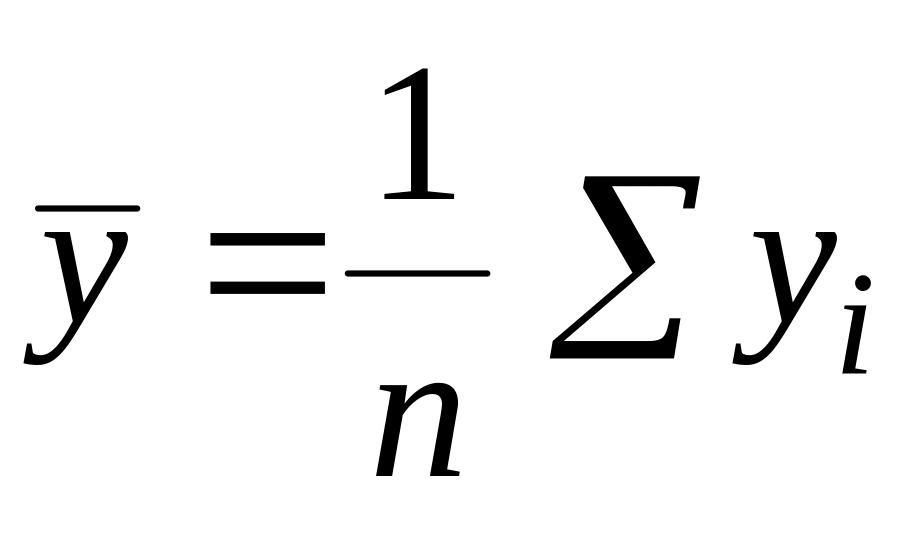 и дисперсии
и дисперсии
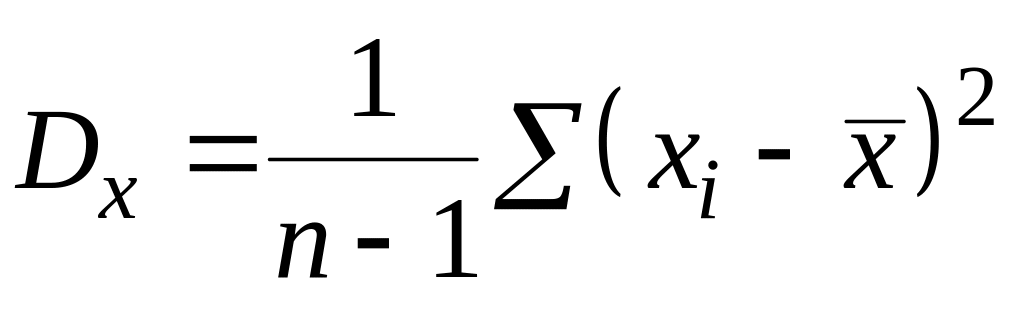 ;
;
 .
.
Таким образом, корреляционный анализ может найти применение в прогнозировании в тех ситуациях, когда на прогнозируемый параметр влияют различные случайные процессы и необходимо оценить степень влияния каждого и ранжировать их.
Пример 1.2. Найдем уравнение регрессии для исследуемой ранее выборки (табл. 1.14).
Таблица 1.14
, МВт |
10,0 |
11,0 |
12,2 |
13,5 |
|
, ГВт·ч |
5,6 |
6,6 |
7,0 |
7,8 |
|
Найдем уравнение линейной регрессии
. (1.29)
Ранее было
получено:  ;
.
;
.
Найдем дисперсии,
смещенные при малой выборке, и стандартные
отклонения
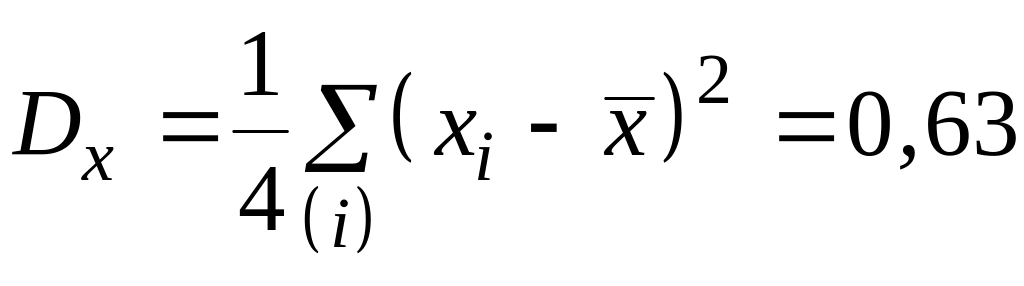 ;
; ![]() ;
;
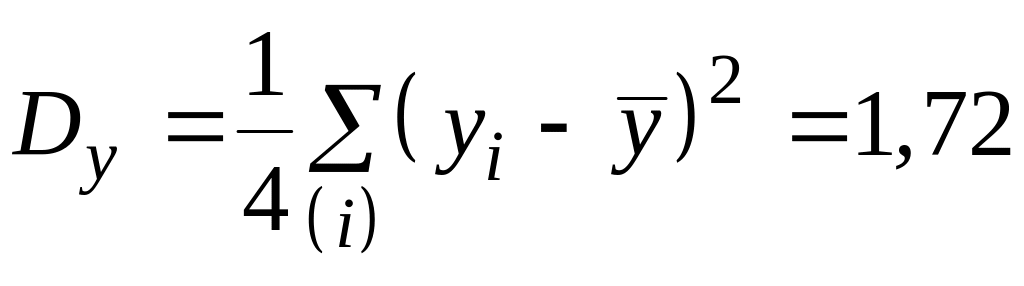 ; δy.
; δy.
Определим коэффициент корреляции:
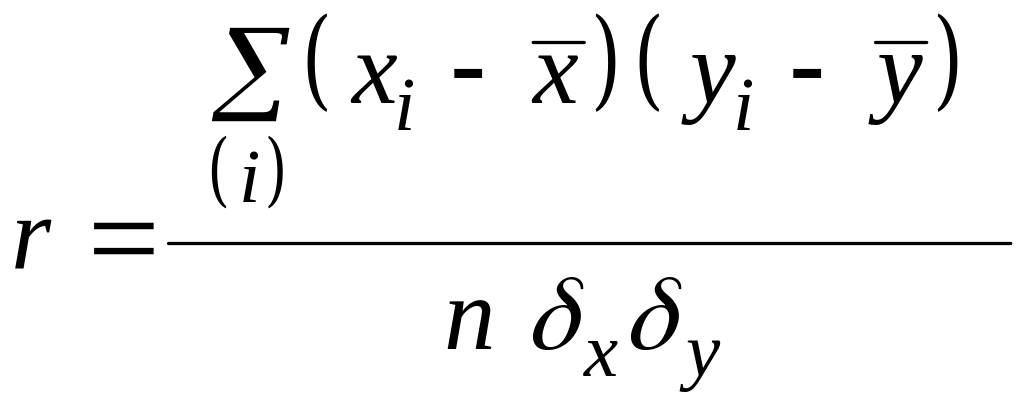 .
(1.30)
.
(1.30)
Подставив числовые значения, получим

что характеризует связь как жесткую и прямо пропорциональную.
Уравнение линейной регрессии
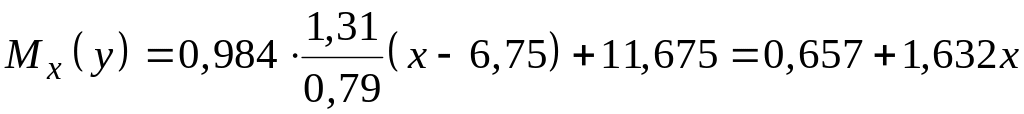 ,
(1.31)
,
(1.31)
или при переходе к параметрам мощности и электроэнергии :
![]() .
.
Сравним полученные результаты.
Таблица 1.15
Метод наименьших квадратов |
Корреляционный анализ |
|
|
|
|
Определить какая из полученных функций даст более точный результат и отдать ей предпочтение на этапе прогнозирования невозможно. Оценку может дать только практика. Ошибки в прогнозах часто определяются за счет неучтенных взаимосвязей. Повысить точность прогноза можно на основе многомерного корреляционного анализа.
1.7. Многомерный корреляционный анализ
Основой многомерного
анализа также является статистическая
выборка, которая может быть представлена
таблицей и обозначена матрицей
![]() :
:
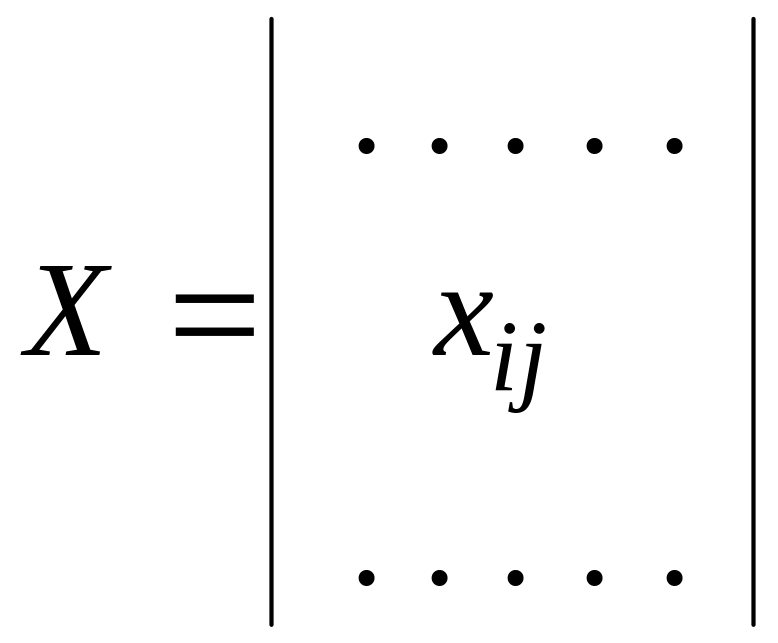 ,
,
где ![]() – номер наблюдения (строка);
– номер наблюдения (строка);
![]() – определяет параметр наблюдения
(столбец).
– определяет параметр наблюдения
(столбец).
Здесь определяются корреляционные связи между каждой парой параметров, расположенных в столбцах k и j. Соответствующие коэффициенты корреляции рассчитываются по формулам парной корреляции
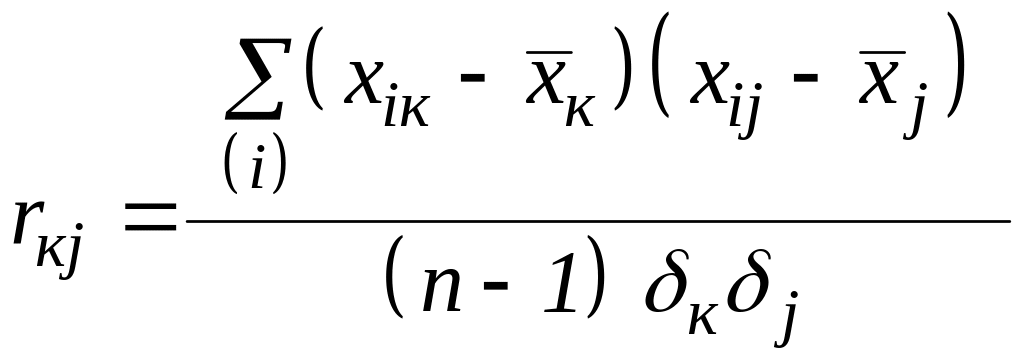 ,
(1.32)
,
(1.32)
где
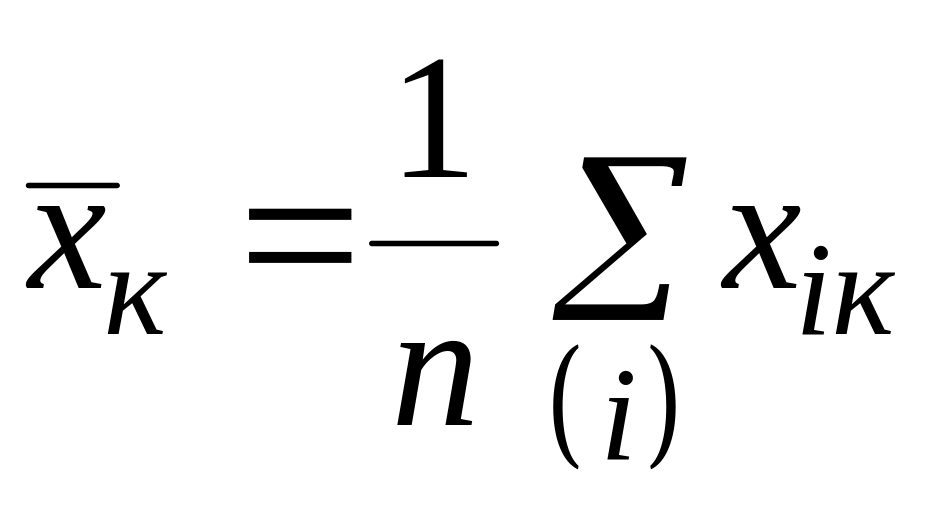 и
и
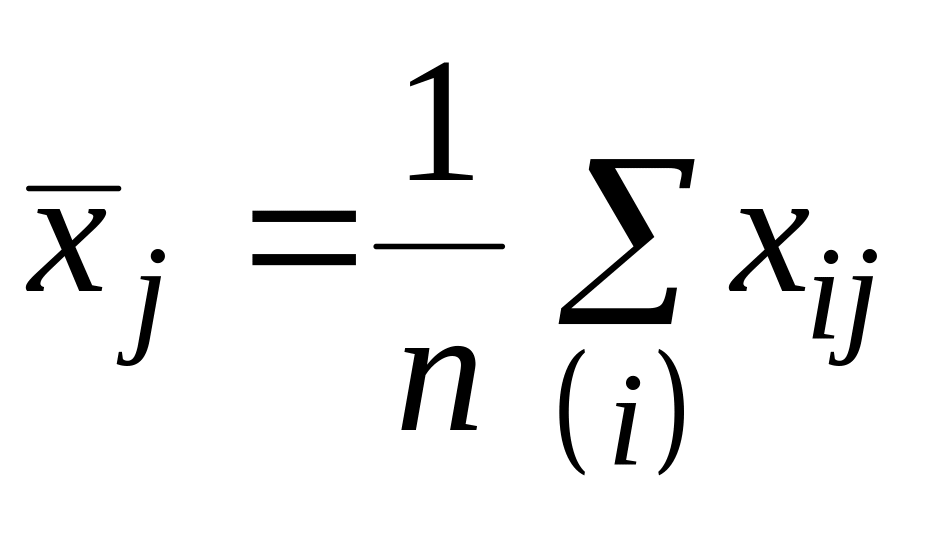 -
средние значения параметров;
-
средние значения параметров;
 ,
,
![]() - дисперсия и отклонение параметра k,
- дисперсия и отклонение параметра k,
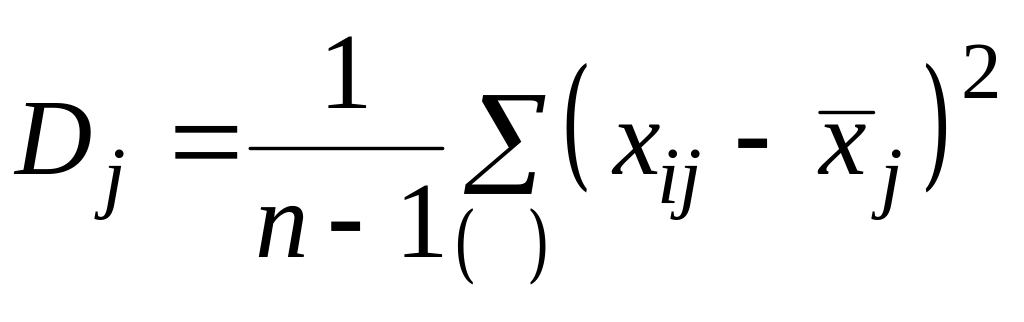 ,
,
![]() -
дисперсия
и отклонение параметра j.
-
дисперсия
и отклонение параметра j.
В результате расчетов находится матрица коэффициентов корреляции, которая всегда квадратная и симметричная относительно главной диагонали
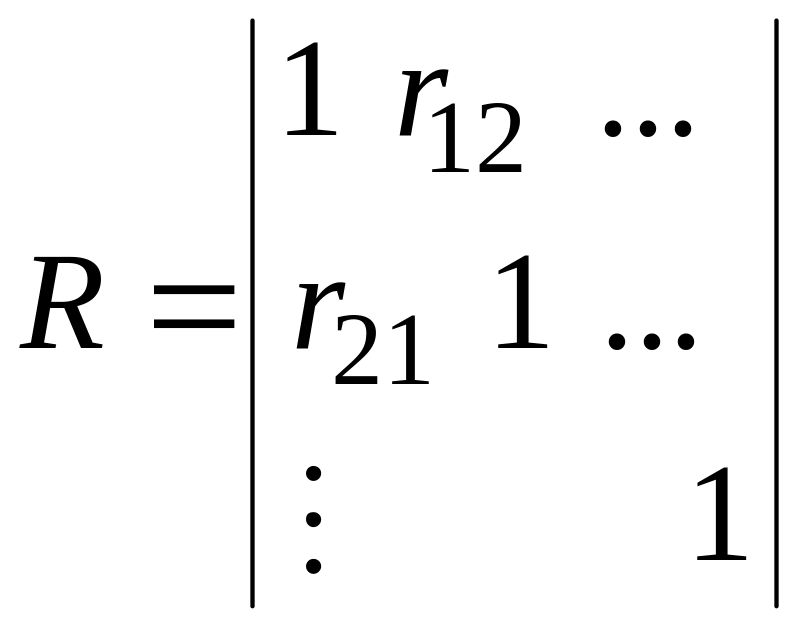 .
.
Порядок матрицы
![]() определяется числом параметров. Ее
анализ позволяет выявить те параметры,
которые наиболее сильно влияют на
прогнозируемый и при формировании
уравнения регрессии не учитывать те,
которые слабо влияют. Тем не менее,
определить уравнение регрессии достаточно
сложно. Например, при влиянии двух
параметров x2
и x3
на прогнозируемый x1,
уравнение регрессии определяется как
сумма:
определяется числом параметров. Ее
анализ позволяет выявить те параметры,
которые наиболее сильно влияют на
прогнозируемый и при формировании
уравнения регрессии не учитывать те,
которые слабо влияют. Тем не менее,
определить уравнение регрессии достаточно
сложно. Например, при влиянии двух
параметров x2
и x3
на прогнозируемый x1,
уравнение регрессии определяется как
сумма:
![]() ,
(1.33)
,
(1.33)
причем коэффициенты определяются следующим образом:
 ;
;
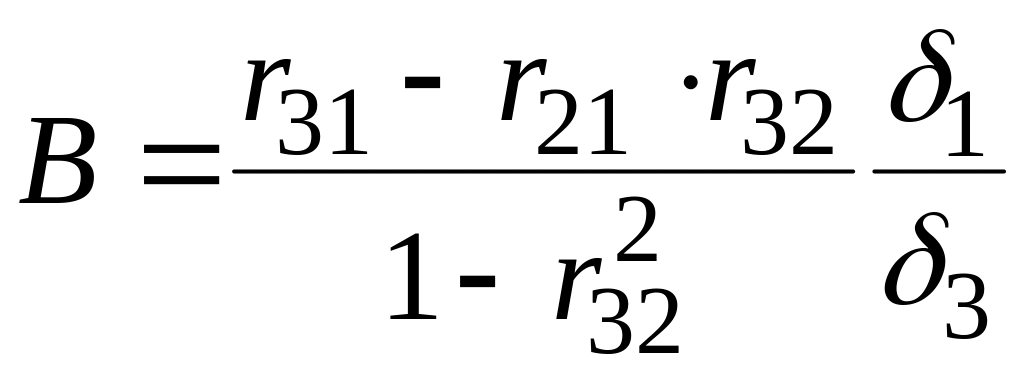 .
(1.35)
.
(1.35)
Пример 1.3.
Для предприятия по результатам наблюдений
получена выборка, связывающая потребляемую
электроэнергию
,
выпуск готовой продукции
![]() и температуру
на улице.
и температуру
на улице.
Таблица 1.16
-
Вид выборки
1
100
10
300
обучающая выборка
2
110
-10
270
3
60
18
150
4
70
20
200
экзаменационная выборка
Обычно для проверки качеств уравнения регрессии исходную выборку делят на две части. Большую часть называют обучающей, а оставшуюся – экзаменационной. И хотя наша выборка далеко не представительная, тем не менее, выделим в ней и экзаменационную часть.
Определим среднее значение для параметров по обучающей выборке:
 .
.
Дисперсия:
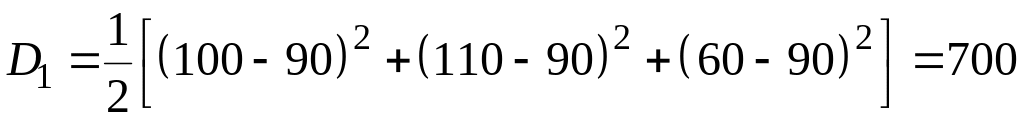 .
.
Стандартное отклонение:
![]() .
.
Аналогично для
![]() и
и
![]() :
:
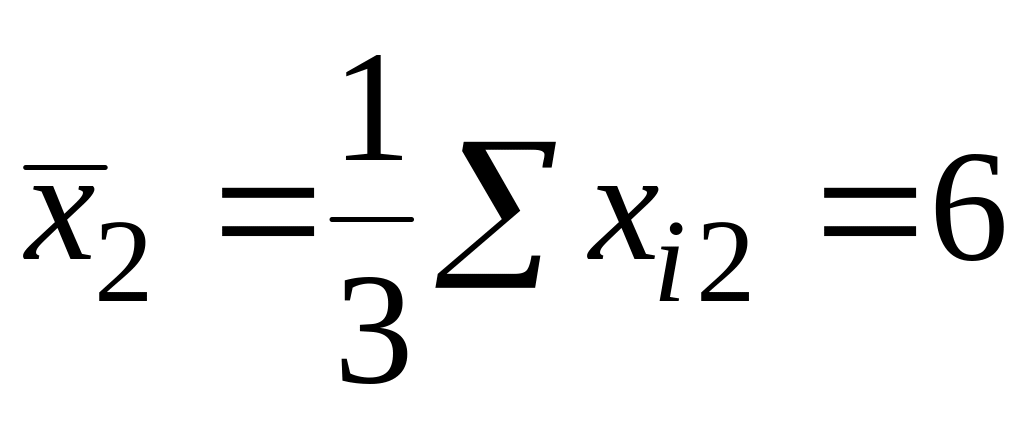 ;
;
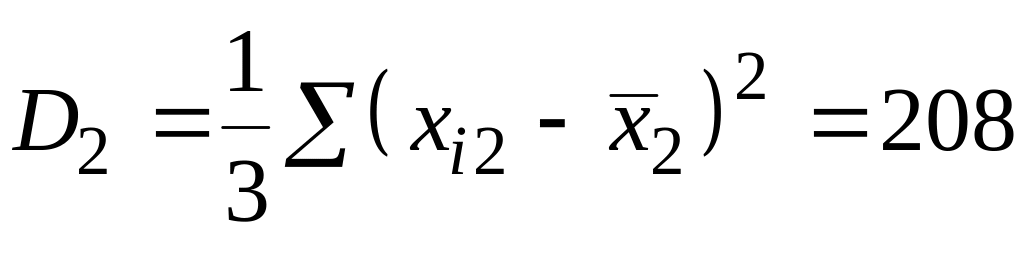 ;
;
![]() ;
;
![]() ;
;
![]() и
и
![]() .
.
Рассчитаем коэффициенты парной корреляции:
между и параметрами:
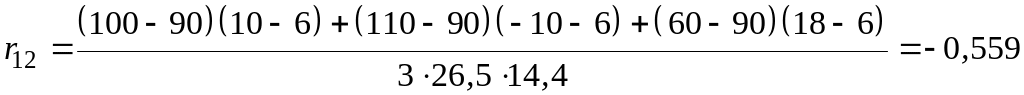
между и :
 ;
;
между и :
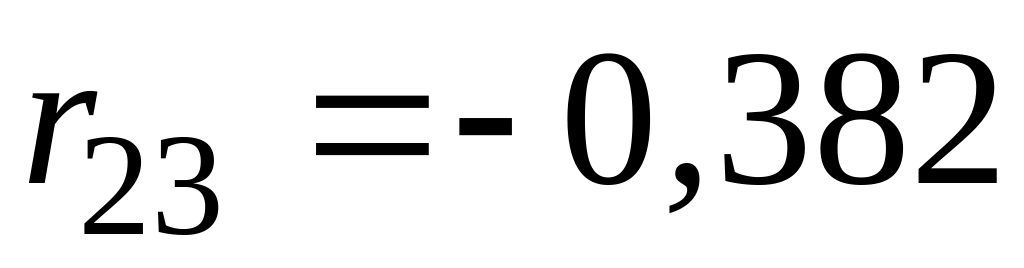 .
.
Треугольник матрицы коэффициентов корреляции будет выглядеть таким образом:
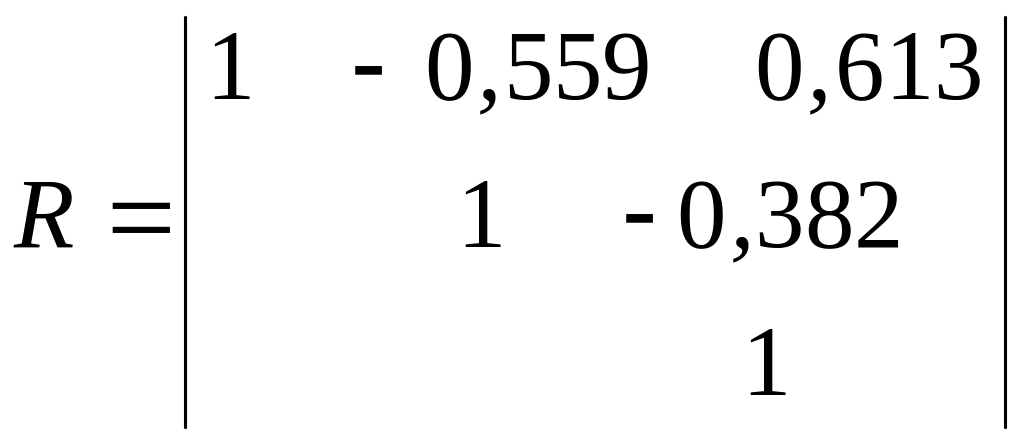 .
.
Остается найти уравнение регрессии:
![]()
![]()
Таким образом, уравнение регрессии:
![]() .
(1.36)
.
(1.36)
Проверим корректность его по экзаменационной выборке (см. табл. 1.16):
![]() .
.
Для принятой далеко не представительной выборки результат можно считать вполне удовлетворительным.
Рассмотренные методы являются далеко не единственными, но они дают представление о сути экстраполяционных методов прогнозирования. Сегодня для целей прогнозирования графиков потребления электроэнергии начинают применяться новые методы на основе искусственных нейронных сетей и другие интеллектуальные методы.
1.8 Прогнозирование графиков нагрузок с применением ИНС
Одной из задач управления режимами энергосистем на ближайшую перспективу, измеряемую часами, сутками, неделями, является прогнозирование графика потребления. Для этой цели используются архивные данные, которые формируются на основе телеметрии по фактическим параметрам прошедших режимов. На серверах оперативно-информационных комплексов хранятся ретроспективные данные за период, измеряемый годами.
Для определения входных переменных нейронной сети при решении задач прогнозирования нагрузки используется модель, описывающая изменение во времени фактических значений нагрузки, которая представляется нелинейной функцией:
![]() ,
(1.37)
,
(1.37)
где Pt – фактическая нагрузка системы в момент времени t; t – текущее время на момент прогноза; Pt−n– предшествующие наблюдения нагрузки; Нt−n –предшествующие наблюдения внешних факторов (температуры окружающей среды, влажности, ветра), влияющих на нагрузку; n – глубина ретроспекции.
На основании выражения (1.37) первой переменной, которая должна быть использована в качестве входа, является сама нагрузка. Например, для суточного графика при часовом разрезе число входов будет равно 24. Вопрос учета числа и состава предшествующих наблюдений нагрузки, как и учета внешних факторов, в каждой задаче решается по-своему. Второй входной переменной, как правило, должна быть температура окружающей среды, влияющая на уровень потребления. В большинстве случаев других параметров погодных условий, как правило, в наличии попросту нет. Кроме того, в качестве входных переменных могут быть использованы параметры, связанные с сезоном года, например, долгота дня, или социальные факторы, например, рабочий или праздничный день, день недели и т.п.
Выходной слой в этой задаче должен содержать 24 нейрона. Обученная ИНС может использоваться для целей прогнозирования длительное время, пока результаты прогноза будут подтверждаться с приемлемой точностью.
Модель долгосрочного прогнозирования формируется для временных диапазонов месяц-квартал-год и используется для планирования технико-экономических показателей работы, а также для составления графиков ремонтов основного оборудования. Прогнозируемыми показателями являются месячное электропотребление (Рср), максимальная и минимальная нагрузки за месяц (Pmax и Pmin ) и коэффициенты, характеризующие график электропотребления: коэффициент неравномерности месячного графика нагрузки α= Pmin /Pmax и коэффициент заполнения месячного графика нагрузки β= Рср/Pmax.
Входными параметрами для обучения ИНС являются следующие переменные, взятые из архива за предшествующие месяцы сезона, аналогичного прогнозируемому месяцу: электропотребление за месяц, определяемое средней мощностью Рср; максимальная и минимальная нагрузки (Pmax и Pmin ), средняя температура (Tср ), долгота дня (ДД ), количество праздничных дней (ПД ) того же месяца.
Для определения прогноза мощностей, характеризующих потребление, с помощью обученной ИНС на вход ее необходимо ввести дополнительно значения долготы дня и количества праздничных дней, а также прогнозируемую среднюю температуру по данным Гидрометцентра.
2. ОПТИМИЗАЦИОННЫЕ МОДЕЛИ ПЛАНИРОВАНИЯ РАЗВИТИЯ
Математическая модель – система переменных, а также уравнений и неравенств, которые описывают основные свойства системы и ее внутренние и внешние связи. Оптимизационная модель дополняется целевой функцией, которая формализует критерии оптимизации.
При составлении моделей для энергетической отрасли широко используется эквивалентирование с тем, чтобы упростить модель.
Применяется территориальное эквивалентирование, когда близко расположенные объекты объединяются в один. При этом появляется ошибка, связанная с учетом затрат на транспорт электроэнергии (потери, капитальные вложения и др.).
Эквивалентирование внешних связей осуществляется, как правило, заданием объемов обмена ресурсами. При этом задача должна решаться итеративным методом, путем совместного планирования развития связанных систем.
Эквивалентирование внутренних технологических связей осуществляется с помощью удельных расходов, например, топлива на выработку электроэнергии
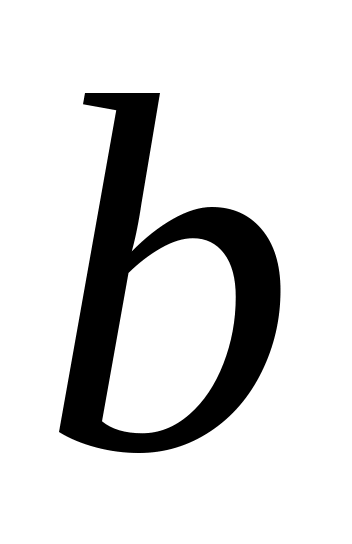 в т у.т. на МВт*ч. Разные технологии
характеризуются разными коэффициентами.
в т у.т. на МВт*ч. Разные технологии
характеризуются разными коэффициентами.
Особое место занимает учет динамики развития системы. Здесь возможно составление динамической модели, где каждый оптимизируемый параметр , например, установленная мощность станции, представляется несколькими переменными, соответствующими мощности этой станции на разных временных разрезах. При этом в целевой функции можно учесть эффект дисконтирования затрат. Недостатком является слишком большая размерность математической модели. Поэтому часто динамику учитывают решением нескольких статических моделей, справедливых для отдельного временного разреза. Например, при
 ,
,
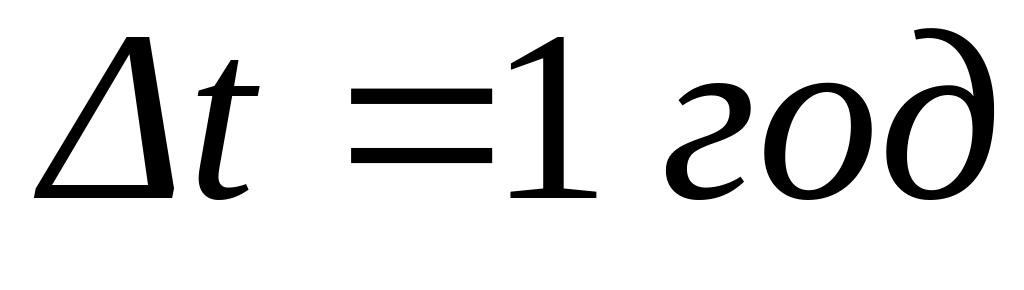 , размерность модели снизится в пять
раз. Правда, полученные решение придется
согласовывать между собой, или, как
говорят, «припасовывать».
, размерность модели снизится в пять
раз. Правда, полученные решение придется
согласовывать между собой, или, как
говорят, «припасовывать».
При построении модели развития глобальной энергетики используется технологическая иерархия. При этом энергетика разделяется на подсистемы:
газовую и газоперерабатывающую;
нефтяную и нефтеперерабатывающую;
угольную и углеперерабатывающую;
электроэнергетическую систему.
Все подсистемы связаны по технологии, и поиск оптимальных путей развития их проводится на основе итерационных процессов.
Оптимизация электроэнергетической системы заключается в выборе структуры развития генерирующих мощностей, выборе развития электрических сетей и выборе сетей электроснабжения предприятий и городов.
Рассмотрим примеры составления моделей, начиная с простейших.
2.1. Линейная модель планирования развития производства
Рассмотрим
простейшую модель на примере энергетического
производства. Предположим, имеется
несколько площадок для возможного
сооружения новых электростанций с
предельной мощностью
![]() с известными удельными затратами
с известными удельными затратами
![]() .
Известно размещение новых нагрузок с
потребностью
.
Известно размещение новых нагрузок с
потребностью
![]() в часы максимума, а также возможные
трассы ЛЭП, связывающие электростанции
и нагрузки, заданной длины
в часы максимума, а также возможные
трассы ЛЭП, связывающие электростанции
и нагрузки, заданной длины
![]() .
Известны удельные затраты на транспорт
.
Известны удельные затраты на транспорт
![]() .
.
Составим линейную оптимизационную модель, позволяющую определить мощность электростанций, направления и объемы передачи мощности по ЛЭП.
В качестве переменных
принимаем
![]() – неизвестные потоки мощности от
-ой
электростанции к
-у
потребителю.
– неизвестные потоки мощности от
-ой
электростанции к
-у
потребителю.
В модели учтем
условие баланса мощностей у потребителей:
![]() ,
. . . ,
,
. . . ,
![]() ,
(2.1)
,
(2.1)
где – число объектов потребления;
ограничение по предельной мощности станций:
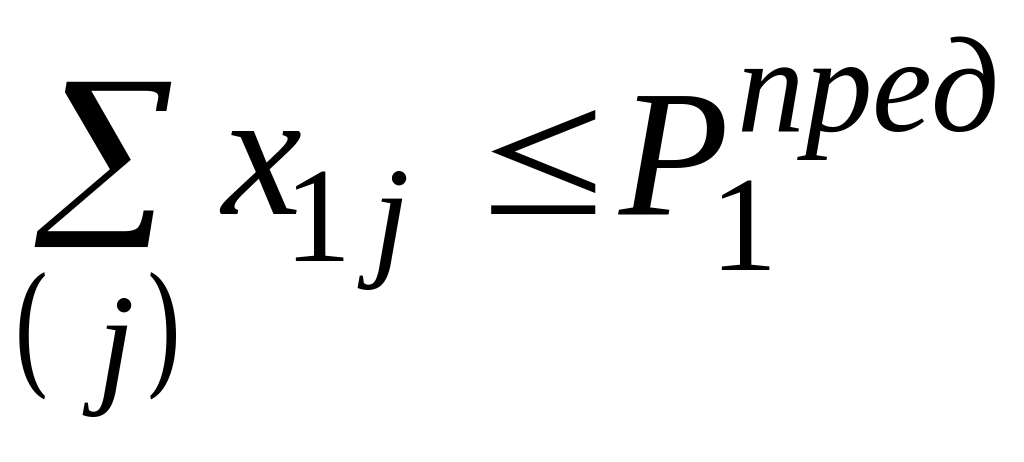 ,…
,
,…
,
 ,
(2.2)
,
(2.2)
где – число площадок для сооружения электростанций.
Целевая функция:
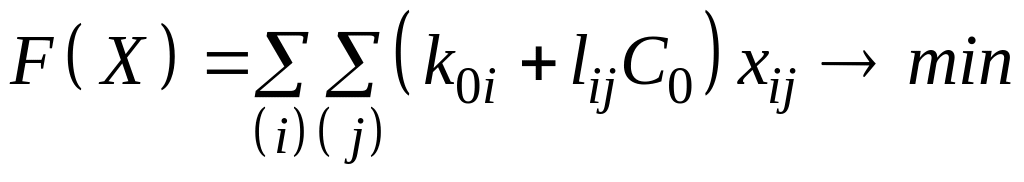 . (2.3)
. (2.3)
Сформулированная
модель является линейной и может решаться
симплекс-методом. Модель имеет все
признаки открытой транспортной задачи,
и может быть решена и методами транспортной
задачи (распределительным или методом
потенциалов). В результате решения
получится достаточно простая схема,
определяемая базисным решением, где
отличными от нуля будут только
![]() переменных из общего числа
переменных из общего числа
![]() .
.
2.2. Линейная модель планирования развития ТЭХ промышленного предприятия
ТЭХ – топливно-энергетическое хозяйство, развитие которого связано с крупными затратами ресурсов. Сегодня существует множество отраслей, теснейшим образом связанных с энергосистемой. Например, металлургическая отрасль. Рассмотрим упрощенную модель металлургического предприятия. Это энергоемкое, многопродуктовое производство (сталь, чугун, прокат различных профилей, кокс, тепло и др.). Предприятие использует различные энергоресурсы: уголь, газ, нефтепродукты, электроэнергию и др. С производством связаны большие затраты. Для оптимизации можно успешно использовать линейные оптимизационные модели.
При составлении
упрощенной модели пройдем по всем этапам
системного анализа. Сначала выделим
объект из общей технико-экономической
системы, частью которой является
предприятие. Внешние связи с поставщиками
ресурсов и потребителями продукции
определим объемами обменных продуктов.
Для упрощения задачи ограничимся
несколькими видами ресурсов. Обозначим
выделяемые объемы угля
![]() ,
газа
,
газа
![]() ,
электроэнергии
,
электроэнергии
![]() ,
а отпуск готовых продуктов:
,
а отпуск готовых продуктов:
![]() –
чугуна,
–
чугуна,
![]() – стали,
– стали,
![]() – тепла. Таким образом, выделяемая
система в результате локализации объекта
может быть представлена «черным ящиком»,
для которого определены лишь внешние
связи (рис.
2.1).
– тепла. Таким образом, выделяемая
система в результате локализации объекта
может быть представлена «черным ящиком»,
для которого определены лишь внешние
связи (рис.
2.1).
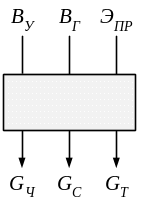
Рис. 2.1
Затем рассматривается
предприятие с его внутренними
технологическими связями. В качестве
неизвестных будем рассматривать все
возможные объемы производства основной
продукции по разным освоенным или
возможным новым технологиям, обозначаемым
индексом
.
Рассмотрим несколько технологий и
введем соответствующие переменные,
определяющие возможные объемы производства
чугуна
![]() по технологии
,
стали
по технологии
,
стали
![]() по технологии
,тепла
на котельной
по технологии
,тепла
на котельной
![]() ,
тепла на ТЭЦ
,
тепла на ТЭЦ
![]() и т.п.
и т.п.
Различные технологии характеризуются удельными расходами первичных ресурсов, а некоторые и возможными выходами вторичных энергоресурсов. Их набор определяется технологическими схемами, которые в наглядной форме представляют технологию предприятия и основные потоки всех видов первичных и вторичных ресурсов и продуктов производства. Без подготовки такой схемы невозможно составление математической модели производства. На рисунке 2.2 показана упрощенная технологическая модель предприятия. В качестве альтернативных источников тепловой энергии рассматриваются котельная и ТЭЦ. Рассматриваемые разные технологии для них могут определяться типом основного оборудования, видом топлива, параметрами пара и т.п. На ТЭЦ в качестве вторичного энергоресурса рассматривается электроэнергия, удельный выход который зависит от типа турбины и параметров пара.
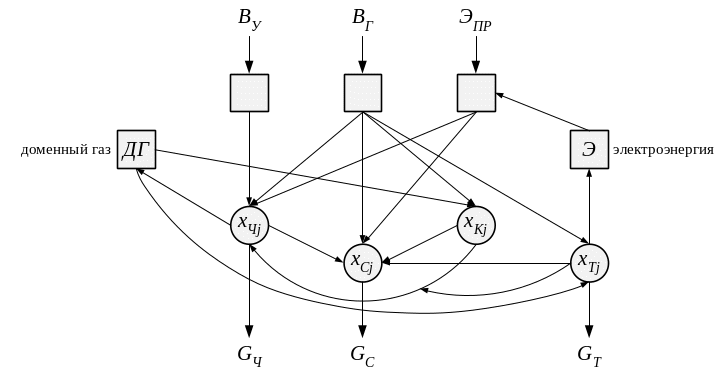
Рис. 2.2
При производстве
чугуна удельные расходы угля, газа,
тепла и электроэнергии обозначим,
соответственно,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Аналогично обозначаются и остальные
удельные расходы, численные значения
которых характеризуют возможные
технологические процессы.
.
Аналогично обозначаются и остальные
удельные расходы, численные значения
которых характеризуют возможные
технологические процессы.
Удельный выход вторичных энергоресурсов обозначим:
![]() –
выход доменного
газа при производстве единицы 1 т чугуна;
–
выход доменного
газа при производстве единицы 1 т чугуна;
![]() – удельный выход
электроэнергии при производстве 1 Гкал
тепла .
– удельный выход
электроэнергии при производстве 1 Гкал
тепла .
В качестве целевой
функции будем учитывать общие внутренние
затраты на производство основной
продукции и затраты на внешние первичные
энергоресурсы. В связи с этим удельные
затраты на производство единицы продукции
по разным технологиям:
![]() ,
,
![]() ,
,
![]() определяются без учета стоимости
первичных энергоресурсов. Для определения
затрат на эти ресурсы используются
тарифы
определяются без учета стоимости
первичных энергоресурсов. Для определения
затрат на эти ресурсы используются
тарифы
![]() ,
,
![]() ,
,
![]() .
.
Опишем основные свойства системы с помощью линейных уравнений и неравенств.
Баланс по чугуну, стали, теплу и коксу, соответственно,
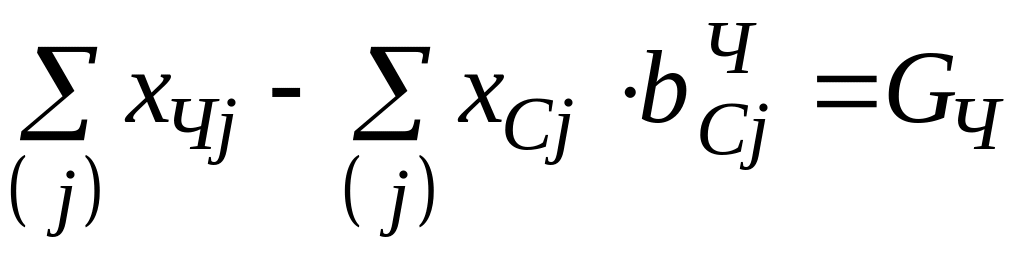 ;
(2.4)
;
(2.4)
![]() ;
(2.5)
;
(2.5)
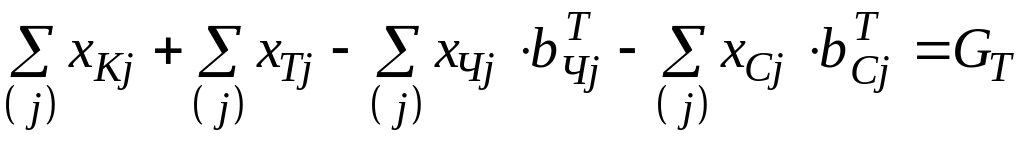 ,
(2.6)
,
(2.6)
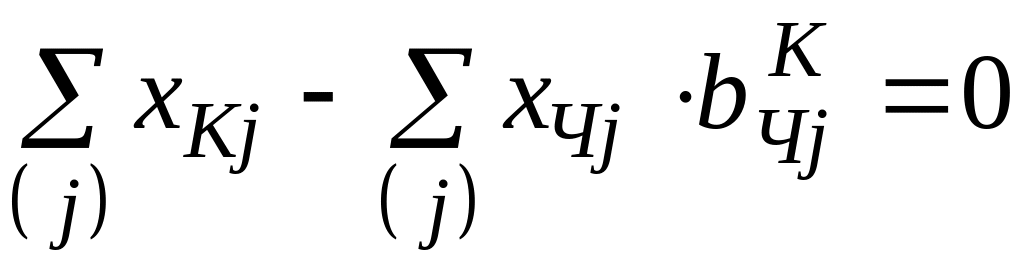 .
(2.7)
.
(2.7)
Баланс по доменному газу
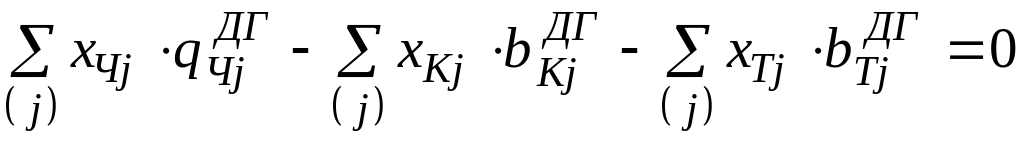 .
(2.8)
.
(2.8)
Баланс по первичным энергоресурсам
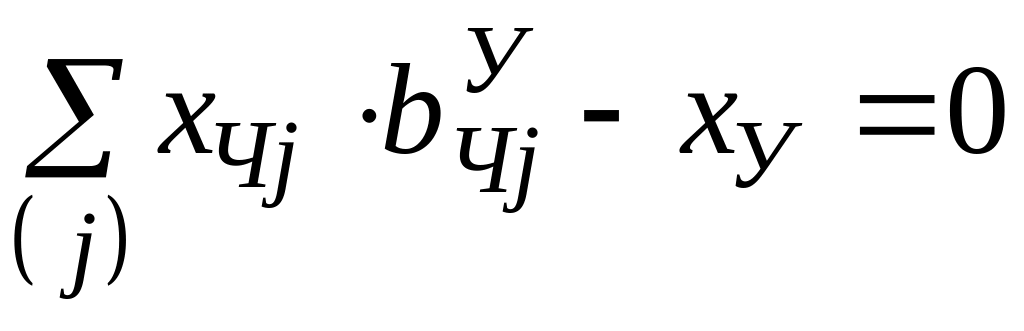 ,
(2.9)
,
(2.9)
где
![]() – объем необходимого для производства
угля;
– объем необходимого для производства
угля;
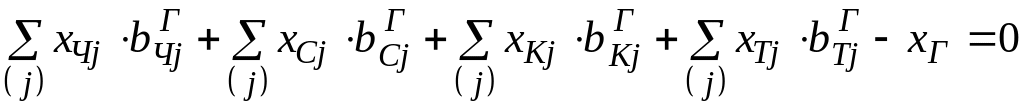 ,
(2.10)
,
(2.10)
где
![]() – необходимый объем газа;
– необходимый объем газа;
 .
(2.11)
.
(2.11)
Ограничения по выделяемым первичным энергоресурсам:
![]() ,
,
![]() ,
,
![]() .
.
Составим целевую функцию. Учтем затраты на основное производство и на первичные ресурсы:
![]() .
.
Сформулированная задача упрощена до предела и может решаться симплекс-методом, что позволит определить наилучшие технологии и обеспечить минимизацию общих затрат на развитие производства. На примере этой задачи видно, что в составлении математической модели необходимо участие технологов. Только в этом случае можно обеспечить экономический эффект.
2.3. Учет затрат в ЛЭП
При составлении математических моделей развития энергосистемы учитываются затраты, связанные с вводом новых мощностей на электростанциях, затраты на добычу и транспорт топлива и затраты в ЛЭП. Затраты в ЛЭП определяются сечением, типом опор и передаваемой мощностью. При планировании заранее не известно сечение ЛЭП, следовательно, затраты в линию необходимо представить функцией только от мощности, исключив сечение, но сохранив возможность определения сечения по найденному в результате решения потоку. Для этой цели может использоваться известный метод экономических интервалов. Рассмотрим суть этого метода.
Затраты на
![]() ЛЭП определенного типа (например, на
железобетонных опорах) сечением
ЛЭП определенного типа (например, на
железобетонных опорах) сечением
![]() как
известно, определяются как приведенные
затраты:
как
известно, определяются как приведенные
затраты:
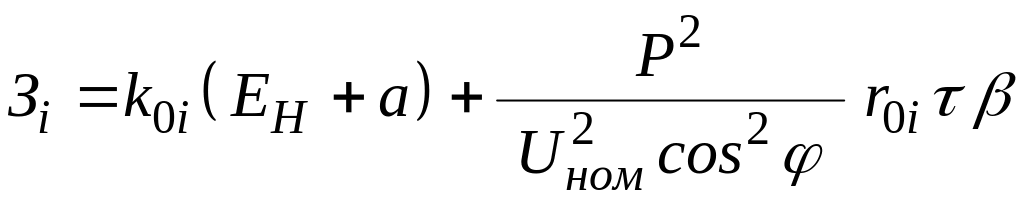 ,
(2.12)
,
(2.12)
где ![]() – удельные затраты;
– удельные затраты;
![]() – нормативный коэффициент;
– нормативный коэффициент;
![]() – коэффициент амортизационных отчислений;
– коэффициент амортизационных отчислений;
![]() – стоимость
потерянной электроэнергии,
– стоимость
потерянной электроэнергии,
– число часов набольших потерь.
Если построить зависимости для всех
сечений, допустимых для принятого
напряжения
![]() ,
то получим семейство пересекающихся
парабол. На рисунке 2.3
показаны только 3 сечения.
,
то получим семейство пересекающихся
парабол. На рисунке 2.3
показаны только 3 сечения.

Рис. 2.3
Точки пересечения определяют границы экономических интервалов по мощности , которые целесообразны для каждого сечения. Они приведены в различных справочниках по проектированию электроэнергетических систем.
Таким образом,
верхняя граница экономического интервала
для сечения
![]() определяется равенством затрат для
-го
и
определяется равенством затрат для
-го
и
![]() -го
сечения
-го
сечения![]() :
:
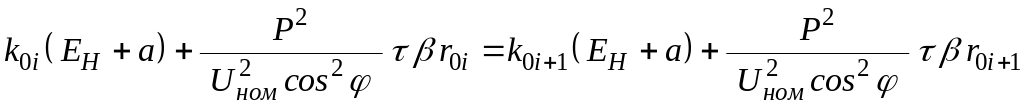 .
.
Из этого условия можно получить:
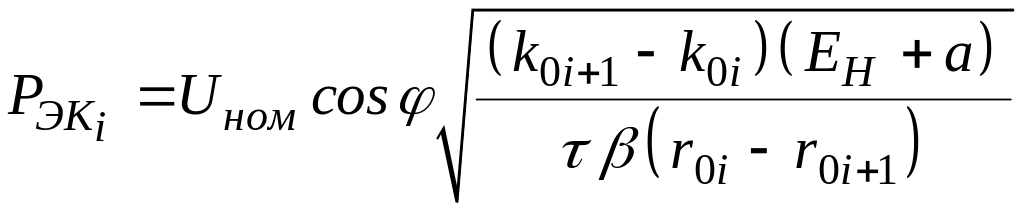 .
(2.13)
.
(2.13)
Условием существования экономического интервала будет условие:
![]() ,
,
что определяется
соотношением
![]() и
и
![]() :
:
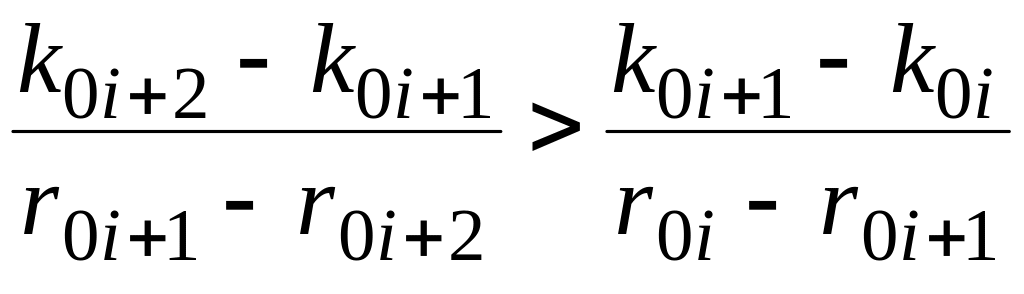 .
.
С помощью таблиц экономических интервалов по найденному в результате решения модели потоку однозначно можно выбрать сечение.
Функция минимальных затрат от определяется нижней огибающей затрат для разных сечений (см. рис. 2.3). Она неудобна для использования в моделях, т.к. на границах интервалов кривая меняет изгиб, и производные имеют разрыв. Поэтому нижнюю огибающую аппроксимируют плавной зависимостью. В качестве предикторов при этом можно принять:
 , что обеспечивает
достаточно высокую точность, но может
использоваться в нелинейных моделях;
, что обеспечивает
достаточно высокую точность, но может
использоваться в нелинейных моделях;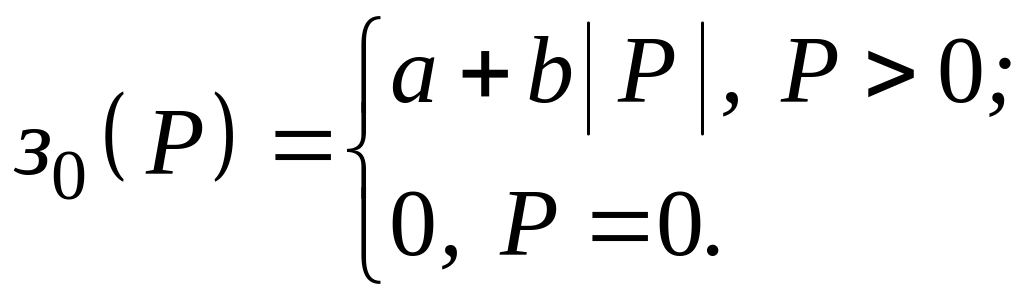 – имеет неплохую
точность, но разрыв при
– имеет неплохую
точность, но разрыв при
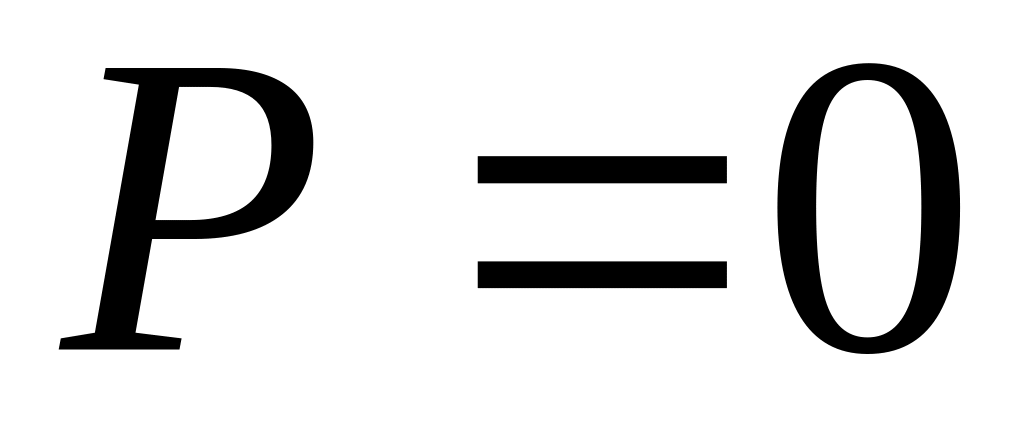 не позволяет использовать его в простых
линейных моделях.
не позволяет использовать его в простых
линейных моделях.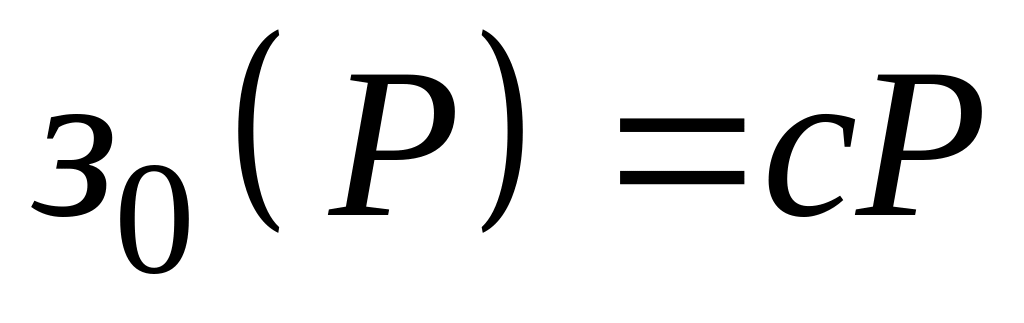 – предиктор
рассчитан на линейные модели, но грубо
представляет затраты, особенно в
диапазоне малых мощностей.
– предиктор
рассчитан на линейные модели, но грубо
представляет затраты, особенно в
диапазоне малых мощностей.
Существуют и другие более сложные предикторы, ориентированные все-таки на нелинейные модели.
Определим с помощью метода наименьших
квадратов коэффициент
![]() простейшего предиктора. С этой целью
из нижней огибающей составляется выборка
из 5-6 точек в рабочем диапазоне мощностей.
простейшего предиктора. С этой целью
из нижней огибающей составляется выборка
из 5-6 точек в рабочем диапазоне мощностей.
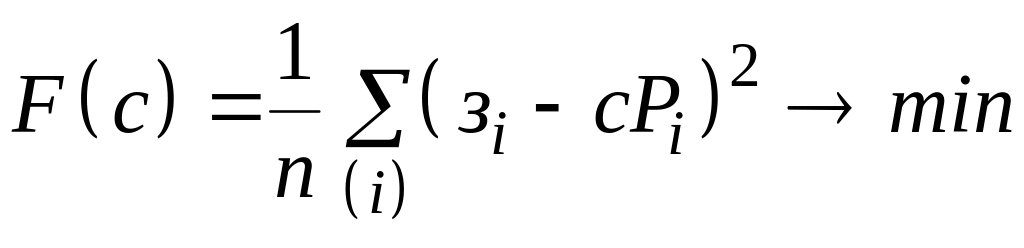 .
(2.14)
.
(2.14)
Условие равенства нулю производной
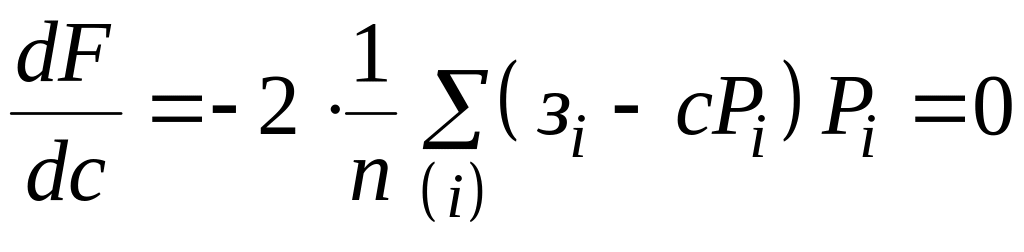
с учетом обозначений
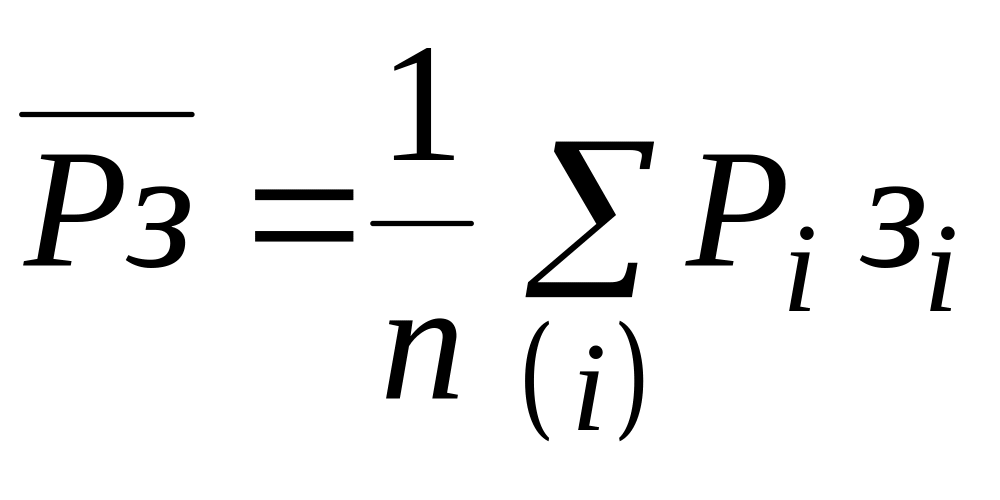 и
и

преобразуем к виду
![]() ,
откуда находим
,
откуда находим
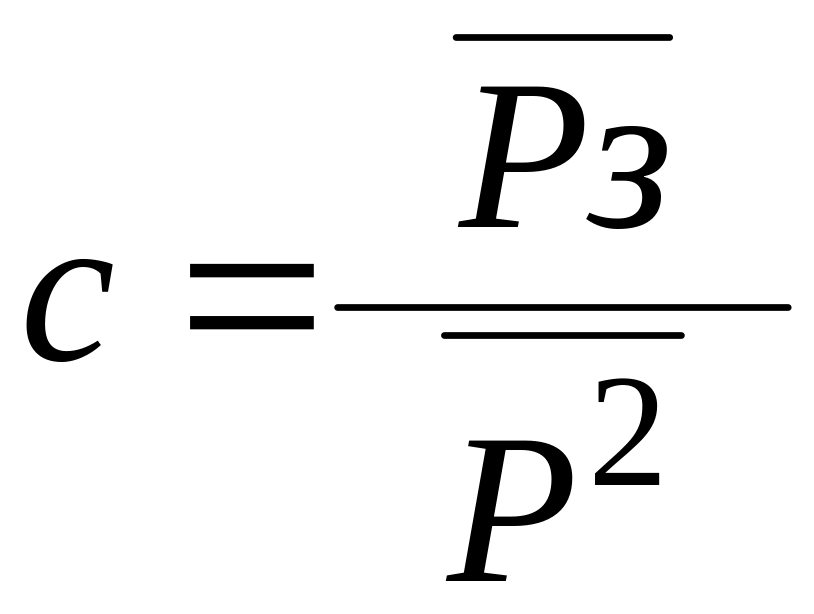 .
.
Пример 2.1.
Определить
удельные затраты в двухцепную ЛЭП
![]() сечением
2×АС-240 при
сечением
2×АС-240 при
![]() МВт.
МВт.
Примем следующие значения технико-экономических показателей:
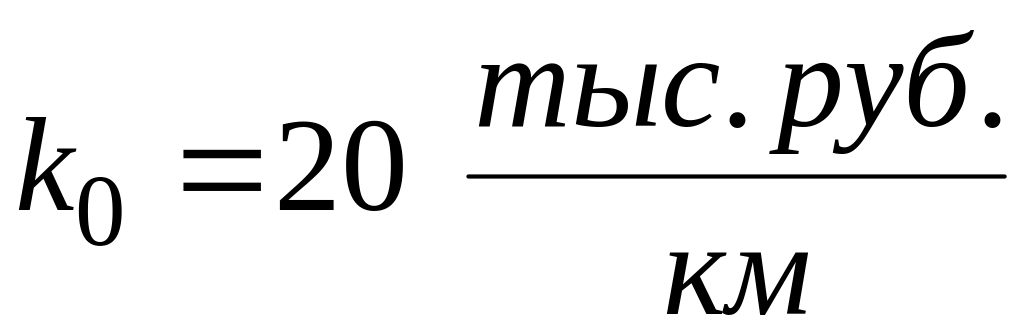 ,
учтем коэффициент инфляции, который
можно принять для Урала и Сибири равным
35.
,
учтем коэффициент инфляции, который
можно принять для Урала и Сибири равным
35.
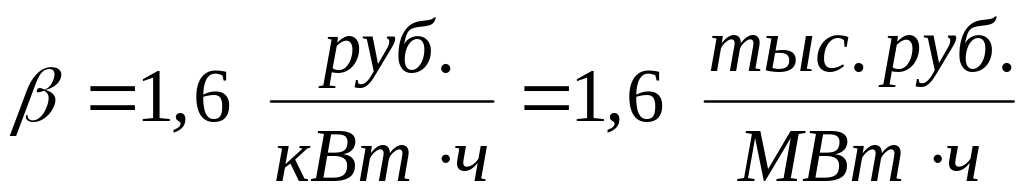 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() для одной цепи АС-240.
для одной цепи АС-240.
Получаем
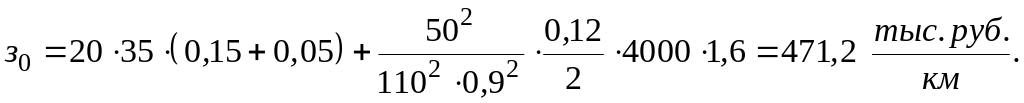
2.4. Линейная оптимизационная динамическая модель выбора структуры генерирующих мощностей и ЛЭП энергосистемы
Обычно планирование
начинается с оценки по прогнозируемым
нагрузкам возможных дефицитов мощности
и энергии для расчетного периода
.
При этом применяется временная ступень
![]() ,
определяющая временные сечения
при составлении модели. Покрытие дефицита
мощности сегодня возможно с использованием
разного типа электростанций: ГЭС, АЭС,
КЭС, ТЭЦ, ПГУ, ГТУ, установок малой
генерации и др.
,
определяющая временные сечения
при составлении модели. Покрытие дефицита
мощности сегодня возможно с использованием
разного типа электростанций: ГЭС, АЭС,
КЭС, ТЭЦ, ПГУ, ГТУ, установок малой
генерации и др.
Сооружение ГЭС планируются особо с учетом притока воды, удобства створа, требований других водопользователей.
АЭС планируются также самостоятельно в моделях развития ядерно-энергетической системы страны;
Решение о строительстве ТЭЦ и малых установок когенерации на промышленных предприятиях принимается в рамках планирования ТЭХ предприятий или городов.
Таким образом, для покрытия дефицита электроэнергии наиболее широко используются ТЭС – КЭС и ПГУ. Коэффициент полезного действия КЭС не превышает 35%, а у ПГУ может достигать 50÷60%.
Составление модели начинается с выбора расчетной схемы, на которой должны быть представлены возможные площадки сооружения станций (ТЭС), возможные базы для поставки топлива и возможные трассы ЛЭП для связи станций (площадок) с известными нагрузками (рис. 2.4)

Рис. 2.4
Исходные данные для планирования включают прогнозируемые технические и экономические показатели. Обозначения, вводимые для этих показателей приведены ниже.
