Раздел 2. Экономический анализ результатов
2.1. Четыре обязательных свойства «Остатков»
Для того чтобы полученное уравнение регрессии было адекватным необходимо, чтобы остаточная компонента удовлетворяла следующим свойствам:
1. Случайность колебаний уровней остаточной последовательности.
2. Соответствие распределения случайной компоненты нормальному закону распределения.
3. Равенство нулю математического ожидания случайной компоненты.
4. Независимость значений уровней случайной компоненты.
Рассмотрим способы проверки этих свойств:
1)
Для
исследования случайности отклонений
от уравнения регрессии находят разности
ɛi=
yi
-
.
В данной задаче используется критерий
серий, основанный на медиане выборки.
Выборка признается случайной, если для
5% уровня значимости выполняются следующие
неравенства :
Кmax < [3,3lg(n+1)] ; ν > [1/2 (n+1-1,96√n-1)],
где Кmax- общая протяженность самой длинной серии, а ν- общее число серий. В работе вычислены результаты, согласно которым Кmax=2 < 4,
а ν= 14> 6. Отсюда следует, что данная модель отвечает первому свойству.
2) Проверка второго свойства производится с помощью нахождения показателей асимметрии γ1 и эксцесса γ2. В качестве оценки асимметрии используются формулы :
,
,
,
+
,
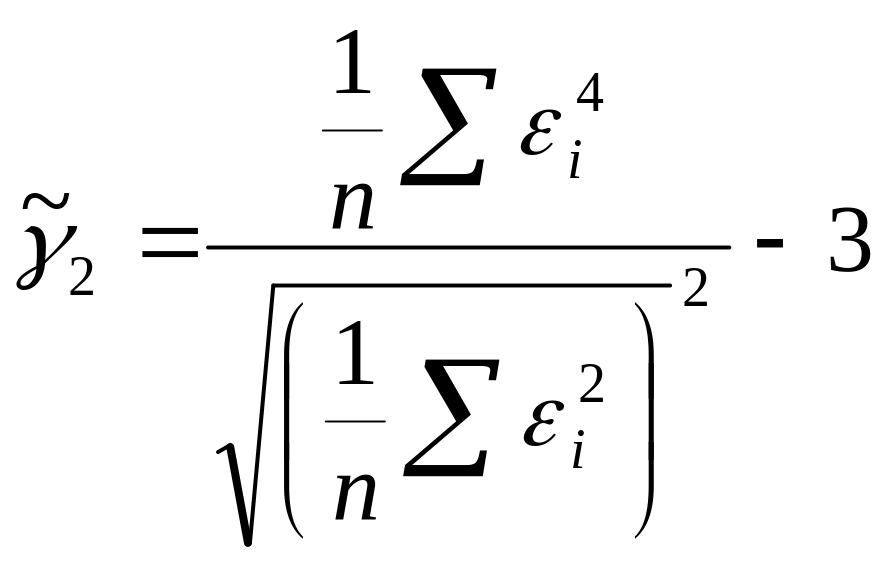где γ1
и γ2
– выборочные характеристики асимметрии,
а σy1
и
σy2
их
среднеквадратические ошибки.
Если
одновременно выполняются условия |
|
< 1,5 σy2
,
и
<1,5
σy2
то
гипотеза о нормальном распределении
принимается. В данной работе
=
-0,4;
=0,59,
σy1
=0,47,
σy2
=0,76,
=0,88;
1,5* σy1=0,71;
1,5* σy2=1,14.
Гипотеза выполняется, соответственно данная модель отвечает второму свойству.
3)Проверка
адекватности осуществляется на основе
t-
критерия Стьюдента по формуле
,
где
- среднее арифметическое значение, а
Sɛ-
стандартное среднеквадратическое
отклонение для этой последовательности.
В данной работе
=
2,84217Е-14, Sɛ=51,48.
Т.к. расчетное t
= 2,47206E-15
меньше табличного, то гипотеза о равенстве нулю математического ожидания случайной последовательности принимается.
4)Проверка независимости значений уровней случайной компоненты производится на основе d – критерия Дарбина – Уотсона по формуле:
Далее
сравниваем полученное значение с
критическими верхним d2
и
нижним d1
.
В работе получено значение d
= 1,74,т.к.
2,26;
(4-2,26)=1,74. Это значение больше верхнего
табличного d2,
а значит, гипотеза о независимости
уровней остаточной последовательности
принимается.
Вывод: все 4 проверки свойств остаточной последовательности дали положительный результат, а значит, модель адекватна.
2.2. Получение модели для преобразованных исходных данных
Мы находим средние величины Y, X2, X3, используя следующие формулы:
,
,
Таблица №6
|
|
|
755,002 |
344,35
|
17,91075
|
Используем формулы:
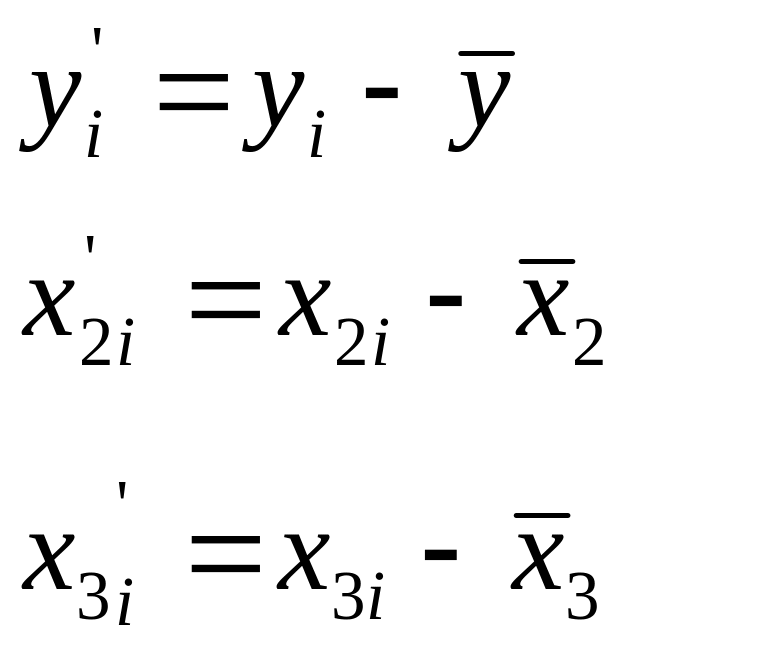
Таблица №7
Получаем:
Производительность(Y`) |
Фондовооруженность(X2`) |
Процент прибыли(X3`) |
-498,592 |
-244,35 |
-13,51075 |
-515,992 |
-224,35 |
-14,61075 |
-442,702 |
-174,35 |
-11,86075 |
-187,102 |
-114,35 |
-5,81075 |
-7,802 |
5,65 |
1,33925 |
-417,302 |
-174,35 |
-12,96075 |
-484,602 |
-194,35 |
-16,09575 |
-252,102 |
-84,35 |
-5,81075 |
106,298 |
125,65 |
-0,86075 |
439,198 |
205,65 |
6,28925 |
-47,022 |
11,65 |
-4,16075 |
449,298 |
426,65 |
4,63925 |
298,198 |
-11,35 |
18,38925 |
53,798 |
-216,35 |
21,13925 |
543,498 |
436,65 |
-2,51075 |
139,738 |
12,65 |
7,93925 |
408,098 |
99,65 |
13,43925 |
1,798 |
-75,35 |
1,88925 |
720,598 |
321,65 |
21,13925 |
-307,302 |
-132,35 |
-8,01075 |
На основании данных таблицы получаем результаты расчета коэффициентов уравнения регрессии и статистических характеристик:
Таблица 8
ВЫВОД ИТОГОВ |
|
|
|
Регрессионная статистика |
|
Множественный R |
0,991033691 |
R-квадрат |
0,982147776 |
Нормированный R-квадрат |
0,980047515 |
Стандартная ошибка |
54,35745149 |
Наблюдения |
20 |
Дисперсионный анализ |
|
|
|
|
|
|
df |
SS |
MS |
F |
Значимость F |
Регрессия |
2 |
2763450,013 |
1381725,007 |
467,6311616 |
1,37843E-15 |
Остаток |
17 |
50230,45306 |
2954,732533 |
|
|
Итого |
19 |
2813680,466 |
|
|
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Y-пересечение |
8,11054E-14 |
12,15469566 |
6,67276E-15 |
1 |
X2` |
1,182454589 |
0,066494058 |
17,78286096 |
2,02289E-12 |
X3` |
16,62193545 |
1,183634254 |
14,04313486 |
8,77044E-11 |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
-25,64416602 |
25,64416602 |
-25,64416602 |
25,64416602 |
1,042164391 |
1,322744787 |
1,042164391 |
1,322744787 |
14,12468549 |
19,11918542 |
14,12468549 |
19,11918542 |
Вывод вероятности
Персентиль |
Y` |
2,5 |
-515,992 |
7,5 |
-498,592 |
12,5 |
-484,602 |
17,5 |
-442,702 |
22,5 |
-417,302 |
27,5 |
-307,302 |
32,5 |
-252,102 |
37,5 |
-187,102 |
42,5 |
-47,022 |
47,5 |
-7,802 |
52,5 |
1,798 |
57,5 |
53,798 |
62,5 |
106,298 |
67,5 |
139,738 |
72,5 |
298,198 |
77,5 |
408,098 |
82,5 |
439,198 |
87,5 |
449,298 |
92,5 |
543,498 |
97,5 |
720,598 |
У
равнение
регрессии имеет вид:
В таблице №8 получаем необходимые значения, используя формулы:
y”i=yi/yср.
x’’2i=x2i/x2cp
x”3i=x3i/x3cр
Таблица №8
Производительность(Y``) |
Фондовооруженность(x2``) |
Процент прибыли(x3``) |
0,339614994 |
0,290402207 |
0,245662521 |
0,316568698 |
0,348482648 |
0,184246891 |
0,413641288 |
0,493683752 |
0,337785967 |
0,752183438 |
0,667925076 |
0,675571933 |
0,989666253 |
1,016407725 |
1,07477353 |
0,447283583 |
0,493683752 |
0,276370336 |
0,358144747 |
0,435603311 |
0,10133579 |
0,666090951 |
0,755045738 |
0,675571933 |
1,14079168 |
1,364890373 |
0,951942269 |
1,581717664 |
1,597212139 |
1,351143866 |
0,93771937 |
1,033831857 |
0,767695378 |
1,595095112 |
2,239001016 |
1,259020421 |
1,394963192 |
0,967039349 |
2,026715799 |
1,07125544 |
0,371714825 |
2,180254875 |
1,719862994 |
2,268041237 |
0,859818824 |
1,185082953 |
1,036735879 |
1,443267312 |
1,54052572 |
1,289385799 |
1,750345463 |
1,002381451 |
0,781181937 |
1,105481345 |
1,954431909 |
1,934078699 |
2,180254875 |
0,592978562 |
0,615652679 |
0,552740673 |
Результаты расчета коэффициентов уравнения регрессии и статистических характеристик:
Таблица №9
ВЫВОД ИТОГОВ
Регрессионная статистика |
|
Множественный R |
0,991033691 |
R-квадрат |
0,982147776 |
Нормированный R-квадрат |
0,980047515 |
Стандартная ошибка |
0,071996434 |
Наблюдения |
20 |
Дисперсионный анализ |
|
|
|
|
|
|
df |
SS |
MS |
F |
Значимость F |
Регрессия |
2 |
4,847919604 |
2,423959802 |
467,6311616 |
1,37843E-15 |
Остаток |
17 |
0,08811927 |
0,005183486 |
|
|
Итого |
19 |
4,936038874 |
|
|
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Y-пересечение |
0,066373906 |
0,034514348 |
1,923081554 |
0,071384977 |
x2`` |
0,539307496 |
0,030327375 |
17,78286096 |
2,02289E-12 |
x3`` |
0,394318598 |
0,028079101 |
14,04313486 |
8,77044E-11 |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
-0,006445002 |
0,139192815 |
-0,006445002 |
0,139192815 |
0,475322328 |
0,603292663 |
0,475322328 |
0,603292663 |
0,335076875 |
0,453560322 |
0,335076875 |
0,453560322 |
ВЫВОД ВЕРОЯТНОСТИ
Персентиль |
Y`` |
2,5 |
0,316568698 |
7,5 |
0,339614994 |
12,5 |
0,358144747 |
17,5 |
0,413641288 |
22,5 |
0,447283583 |
27,5 |
0,592978562 |
32,5 |
0,666090951 |
37,5 |
0,752183438 |
42,5 |
0,93771937 |
47,5 |
0,989666253 |
52,5 |
1,002381451 |
57,5 |
1,07125544 |
62,5 |
1,14079168 |
67,5 |
1,185082953 |
72,5 |
1,394963192 |
77,5 |
1,54052572 |
82,5 |
1,581717664 |
87,5 |
1,595095112 |
92,5 |
1,719862994 |
97,5 |
1,954431909 |
Уравнение регрессии имеет вид:
Для нахождения относительных значений мы будем использовать следующие формулы:
а0 = а”0 * уср (2)
b2 = b”2*уср/х2ср (3)
bз = b”з*уср/х3ср (4)
Далее используем формулы 2, 3, 4 и получаем коэффициенты регрессии. Это говорит о том, что все вычисления проведены верно.
Таблица №11
a0 |
50,1123178 |
b2 |
1,16204751 |
b3 |
16,60850539 |