МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Тюменский государственный нефтегазовый университет» Институт кибернетики, информатики и связи

Отделение информационных технологий и вычислительной техники

Теория вероятностей и математическая статистика

Методические указания для самостоятельных работ

по дисциплине «Теория вероятностей и математическая статистика»

для студентов, обучающихся по специальностям 230113 Компьютерные системы и комплексы, 230115 Программирование в компьютерных системах, 230401 Информационные системы (по отраслям)

Составитель Т.В. Цыганова

Тюмень

ТюмГНГУ

2012

Теория вероятностей и математическая статистика: метод. указ. для самостоятельных работ для студентов, обучающихся по спец. 230113 Компьютерные системы и комплексы, 230115 Программирование в компьютерных системах, 230401 Информационные системы (по отраслям) / сост. Т.В.Цыганова; Тюменский государственный нефтегазовый университет.– 1-е изд.– Тюмень: Издательский центр БИК, ТюмГНГУ, 2012.– 22 с.

Методические указания рассмотрены и рекомендованы к изданию на заседании цикловой комиссии отделения информационных технологий и вычислительной техники

«19» июня 2012 года, протокол № 10

Аннотация

Методические указания по дисциплине «Теория вероятностей и математическая статистика» предназначены для студентов, обучающихся по специальностям 230113 Компьютерные системы и комплексы, 230115 Программирование в компьютерных системах, 230401 Информационные системы (по отраслям). Данная дисциплина изучается в двух семестрах.

Приведено содержание основных тем дисциплины, указаны перечень лабораторных работ и темы практических занятий. Приведен список рекомендуемой литературы.

Содержание

Введение	4
Общие требования к оформлению самостоятельной работы	5
Самостоятельная работа №1	5
Самостоятельная работа №2	6
Самостоятельная работа №3	8
Самостоятельная работа №4	11
Самостоятельная работа №5	13
Самостоятельная работа №6	15
Самостоятельная работа №7	16
Самостоятельная работа №8	19
Список рекомендуемой литературы	20

Введение

Учебная дисциплина «Теория вероятностей и математическая статистика» входит в блок общепрофессиональных дисциплин. Данная дисциплина тесно связана с дисциплинами математического профиля.

Самостоятельная работа является одним из видов учебных занятий студентов.

Целью самостоятельных работ является систематизация и закрепление полученных теоретических знаний и практических умений студентов; формирование умений использовать справочную документацию и специальную литературу; развитие познавательных способностей.

При выполнении самостоятельных работ студент должен:

знать:

• классическую формулу определения вероятности;

• формулу полной вероятности;

• формула Байеса;

• числовые характеристики дискретной случайной величины (математическое ожидание, дисперсия, среднее квадратическое отклонение);

уметь:

• определять какой формулой нужно воспользоваться при решении той или иной задачи;

• строить график функции распределения;

• проводить доказательство;

• применять формулы числовых характеристик для дискретных случайных величин.

Настоящие методические рекомендации предназначены для студентов очной формы обучения, обучающихся по специальностям 230115 Программирование в компьютерных системах, 230401 Информационные системы (по отраслям).

ОБЩИЕ ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

Форма отчетности:

• номер и название самостоятельной работы;

• цель работы;

• условия заданий;

• подробное решение заданий;

• список используемой литературы.

САМОСТОЯТЕЛЬНАЯ РАБОТА №1

Тема: Условная вероятность

Цель: сформировать навыки решения задач на применение формул Байеса, полной вероятности.

Время выполнения: 4 часа

Теоретические сведения

Пусть событие А может наступить лишь при условии наступления одного из несовместных событий В₁, В₂, …,В_n. Эти события будем называть предположениями или гипотезами. Они образуют полную группу событий. Вероятность полной группы событий равна 1.

- формула полной вероятности

- Формула Байеса

Пример. из 1-ой во 2-ую перекладывают 2 шара, затем из 2-ой достают 1 шар. Он оказывается белым. Какой состав переложенных шаров наиболее вероятен?

Решение:

А – вынут б.ш. из 2-ой урны

В₁ – переложили 2 б.ш.

В₂ – переложили 2 ч.ш.

В₃ – переложили 1б., 1 ч. шар

Р(В₁)=7/10*6/9=42/90

Р(В₂)=3/10*2/9=6/90

Р(В₃)=7/10*3/9+3/10*7/9=42/90

Р(А/В₁)=8/12

Р(А/В₂)=6/12

Р(А/В₃)=7/12

Р(А)=42/90*8/12+6/90*6/12+42/90*7/12=111/180

Р(В₁/А)=

Ответ: Вероятнее всего переложили 2б. шара

Задание для самостоятельной работы:

Подобрать две задачи на использование формул полной вероятности и Байеса. Оформить согласно требований.

Рекомендуемая литература: 1;2;4.

САМОСТОЯТЕЛЬНАЯ РАБОТА №2

Тема: Вычисление вероятности сложных событий

Цель: сформировать навыки решения задач на применение формулы классического определения вероятности, формул комбинаторики.

Время выполнения: 2 часа (для 230115); 4 часа (для 230401)

Теоретические сведения

Пусть имеется урна с десятью шарами, из которых 6 белых и 4 черных. Тогда возможны следующие события:

А – вынуть белый шар из урны

В – вынуть черный шар из урны

Событие А состоит из событий А₁,А₂, А₃, А₄, А₅, А₆. Событие В состоит из событий В₁, В₂, В₃, В₄. Тогда процент белых шаров в урне определиться как отношение , а процент черных шаров .

Определение: Вероятностью события А наз. число, равное отношению числа исходов m благоприятствующих наступлению события А к общему числу всех элементарных исходов n.

- формула классического способа подсчета вероятности

Вероятность случайного события есть число, заключенное между нулем и единицей

Определение: Перестановки – это комбинации, составленные из всех п элементов данного множества и отличающиеся только порядком их расположения. Число всех возможных перестановок

Р_п = п!

Определение: Размещения – комбинации из т элементов множества, содержащего п различных элементов, отличающиеся либо составом элементов, либо их порядком. Число всех возможных размещений

Определение: Сочетания – неупорядоченные наборы из т элементов множества, содержащего п различных элементов (то есть наборы, отличающиеся только составом элементов). Число сочетаний

Пример 1. В отборочных соревнованиях принимают участие 10 человек, из которых в финал выходят трое. Сколько может быть различных троек финалистов?

Решение. В отличие от предыдущего примера, здесь не важен порядок финалистов, следовательно, ищем число сочетаний из 10 по 3:

Ответ:

Пример 2. В урне 10 шаров: 6белых и 4черных. Из нее вынимают два шара. Какова вероятность того что: а) 2белых; б) 2черных; в) 1белый,1черный

Решение:

а) пусть А – вынуты 2белых шара. Найдем общее число всех элементарных исходов n.

б) пусть В – вынуты 2 черных шара

в) пусть С – вынут 1белый и 1черный шар

n=45

m_c=6*4=24

Ответ: а) б) в)

Задание для самостоятельной работы:

Подобрать три задачи на использование формул комбинаторики, формулы классического способа подсчета вероятностей. Оформить согласно требований.

Рекомендуемая литература: 2;3;4.

САМОСТОЯТЕЛЬНАЯ РАБОТА №3

Тема: График функции распределения для дискретной случайной величины

Цель: сформировать навыки решения на нахождение функции распределения и построения графика ее функции.

Время выполнения: 4 часа

Теоретические сведения

Определение: Функцией распределения F(x) случайной величины Х называется вероятность того, что случайная величина примет значение, меньшее х:

F (x) = p (X < x).

Свойства функции распределения:

1. 0 ≤ F(x) ≤ 1.

Действительно, так как функция распределения представляет собой вероятность, она может принимать только те значения, которые принимает вероятность.

2. Функция распределения является неубывающей функцией, то есть F(x₂) ≥ F(x₁) при х₂ > x₁. Это следует из того, что F(x₂) = p(X < x₂) = p(X < x₁) + p(x₁ ≤ X < x₂) ≥ F(x₁).

3. В частности, если все возможные значения Х лежат на интервале [a, b], то F(x) = 0 при х ≤ а и F(x) = 1 при х ≥ b. Действительно, X < a – событие невозможное, а X < b – достоверное.

4. Вероятность того, что случайная величина примет значение из интервала [a, b], равна разности значений функции распределения на концах интервала: p ( a < X < b ) = F(b) – F(a).

Справедливость этого утверждения следует из определения функции распределения (см. свойство 2).

Для дискретной случайной величины значение F(x) в каждой точке представляет собой сумму вероятностей тех ее возможных значений, которые меньше аргумента функции.

Пример 1. Найдем F(x) по данному закону распределения

хi	0	1	2
pi	0,12	0,46	0,42

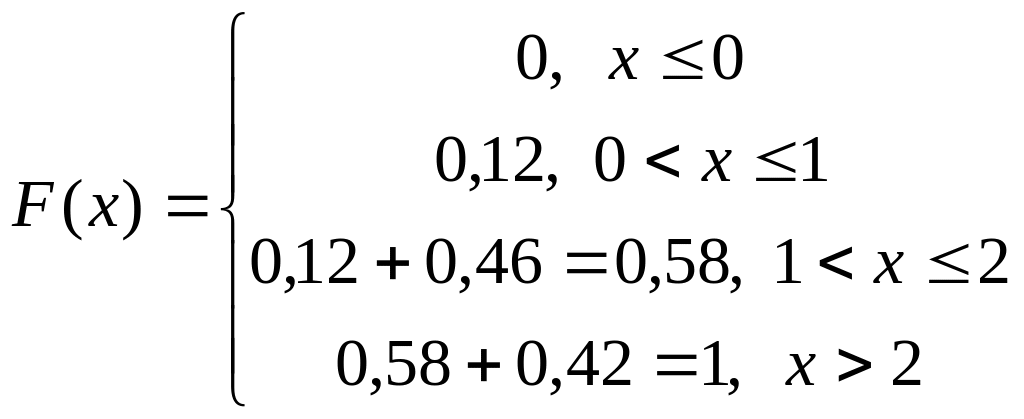
Соответственно график функции распределения имеет ступенчатый вид:

Пример 2. По данному закону распределения найти функцию распределения и построить ее график

х	2	3	4	5	6	7	8	9	10	11	12
р	1/36	2/36	3/36	4/36	5/36	6/36	5/36	4/36	3/36	2/36	1/36

х<2 F(x)=0

2<=x<3 F(x)=1/36

3<=x<4 F(x)=1/36+2/36=3/36

4<=x<5 F(x)=6/36

5<=x<6 F(x)=10/36

6<=x<7 F(x)=15/36

7<=x<8 F(x)=21/36

8<=x<9 F(x)=25/36

9<=x<10 F(x)=30/36

10<=x<11 F(x)=33/36

11<=x<12 F(x)=1