Решение задачи 7

Построить графики функций

1) - этот график получается из графика сдвигом по оси Ох на 2 единицы влево и на 3 единицы вверх по оси Оу.

у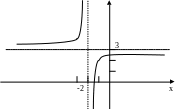

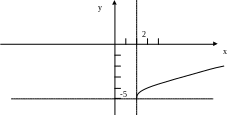
2) - этот график получается из графика сдвигом по оси Ох на 2 единицы вправо и на 5 единиц вниз по оси Оу.

Решение задачи 8

1. ;

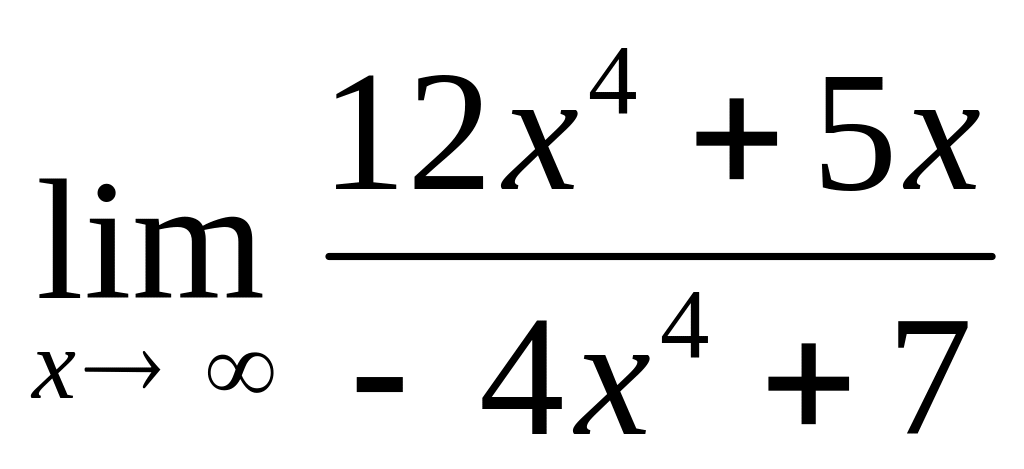Подстановка предельного значения аргумента приводит к неопределённости вида .

Так как под знаком предела стоит отношение двух многочленов, то разделим числитель и знаменатель на старшую степень аргумента, т.е. на . В результате получим

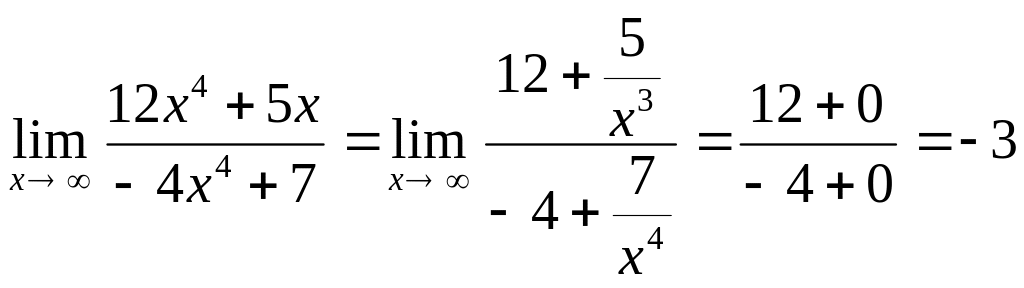, поскольку при функции и являются бесконечно малыми.

2) ;

Подстановка предельного значения аргумента приводит к неопределённости вида . Разложим числитель и знаменатель дроби на множители. Получим

.

3. ;

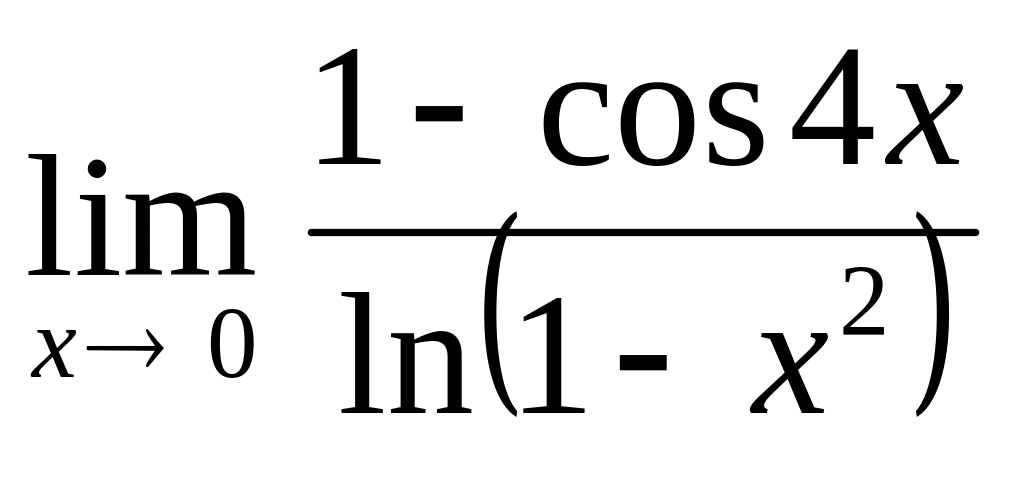Для раскрытия получающейся здесь неопределённости вида используем метод замены бесконечно малых эквивалентными. Так как , то

при , а

. Итак, получаем .

3. 

.

Ответ: 1) –3; 2) 2; 3) –8; 4)

Решение задачи 9

Так как данная функция определена на всей числовой оси, то «подозрительными на разрыв» являются те точки, в которых изменяется аналитическое выражение функции. Т.е. точки х = -1 и х = 0. Вычислим односторонние пределы в этих точках.

Для точки х = -1 имеем

;

.

Односторонние пределы функции в точке х = -1 существуют, но не равны между собой. Следовательно, эта точка является точкой разрыва первого рода.

Для точки х=0 получаем

.

Односторонние пределы функции при равны между собой и равны значению функции в точке х=0: . Следовательно, исследуемая точка является точкой непрерывности.

Построим график данной функции:

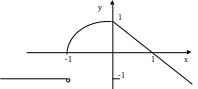
Ответ: функция непрерывна на промежутке и на промежутке ; точка х= -1 является точкой разрыва первого рода.

Решение задачи 10

а)

б)

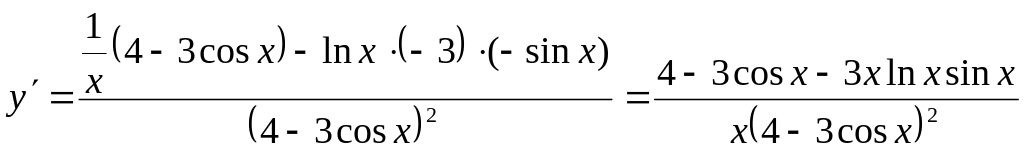
в)

Ответ: а) , б) , в) .

Решение задачи 11

Правило Лопиталя было применено 3 раза.

Ответ: 2.

Решение задачи 12

Исследовать и построить график функции

Решение.

1. Область определения функции D(у)= .

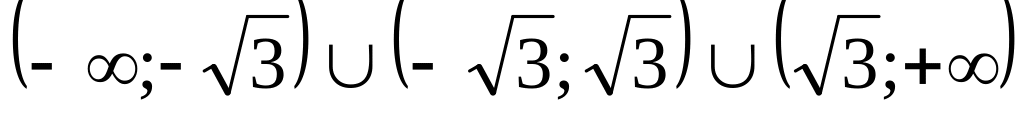2. Находим точки пересечения графика функции с осями координат: если х=0, то у=0; если у=0 , то х=0. Таким образом, график проходит через начало координат

3. Функция не является периодической, так как не существует такого положительного числа Т, что у(х+Т)=у(х).

4. Функция является нечётной, т.к.

1) область определения симметрична относительно начала координат, 2) у(-х)= -у(х).

5. Определим асимптоты графика:

а) Вертикальные асимптоты.

Точки х= и х= - являются точками разрыва функции. Так как и , то прямая х= служит вертикальной асимптотой графика функции. Аналогично найдём односторонние пределы в точке х= - :

и , следовательно, прямая х= - также является вертикальной асимптотой графика функции.

б) горизонтальные асимптоты.

Для нахождения горизонтальной асимптоты вычислим предел функции на бесконечности:

, итак, прямая у=0 – горизонтальная асимптота.

в) Наклонные асимптоты:

у=кх+b – уравнение наклонной асимптоты

наклонной асимптоты нет (она совпадает с горизонтальной у=0).

6. Исследуем функцию на монотонность и экстремум:

;

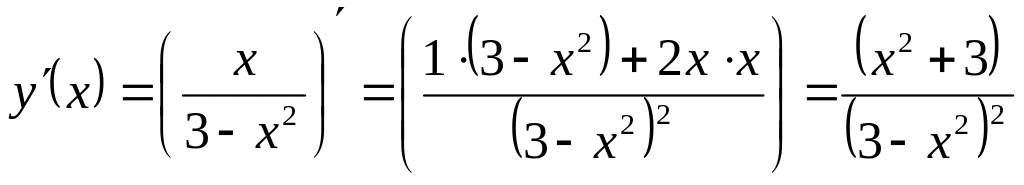Найдём критические точки из условий или не существует:

равенство не выполняется ни при каких х;

не существует при х= и х= - .

Итак, критические точки: х= и х= - .

Составим таблицу

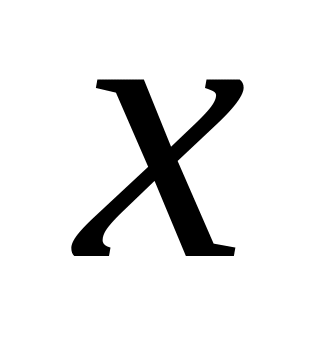
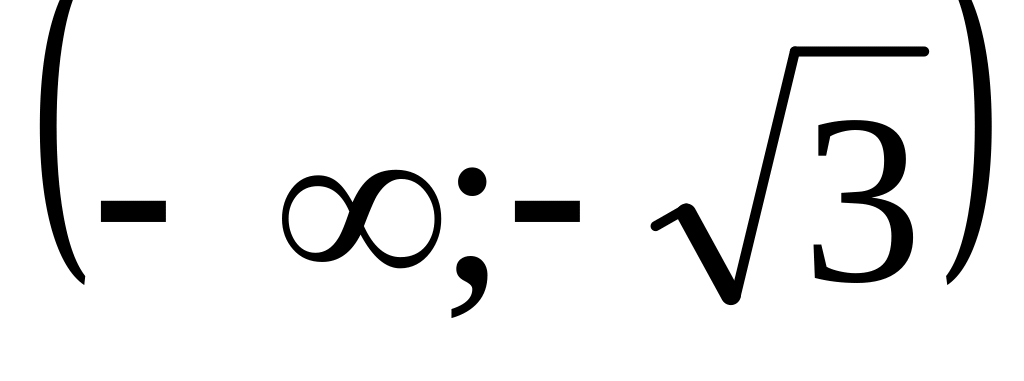
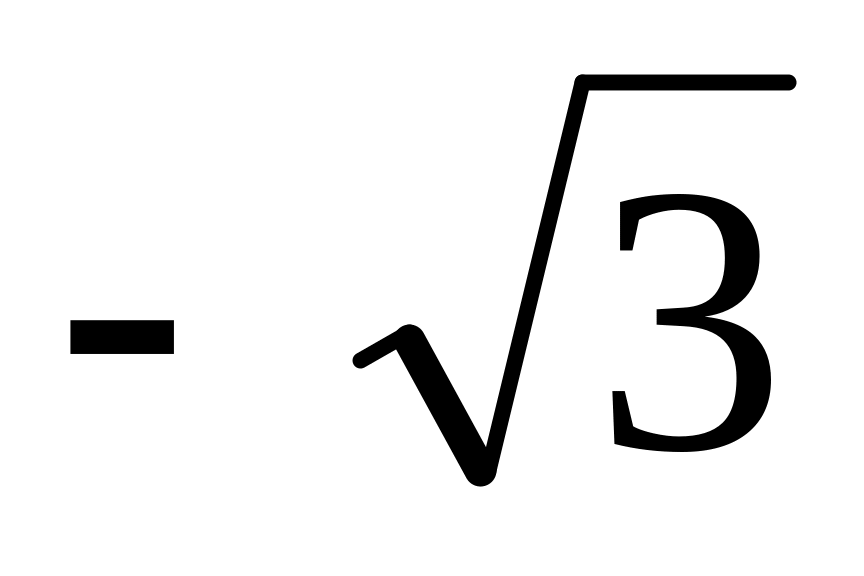
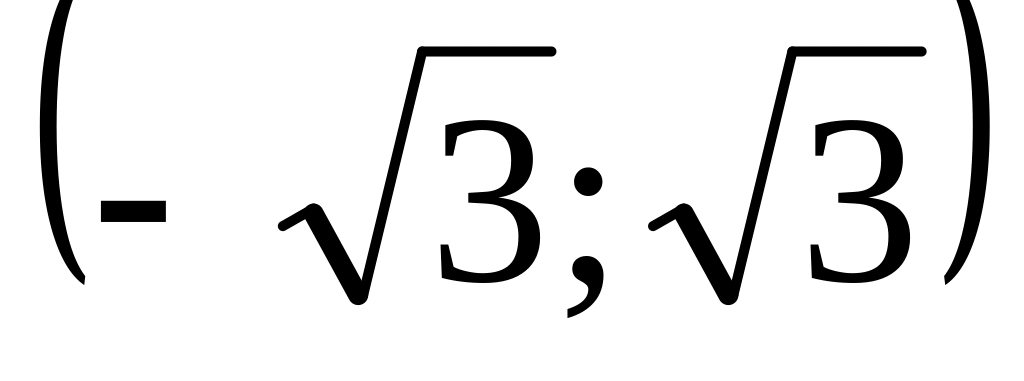
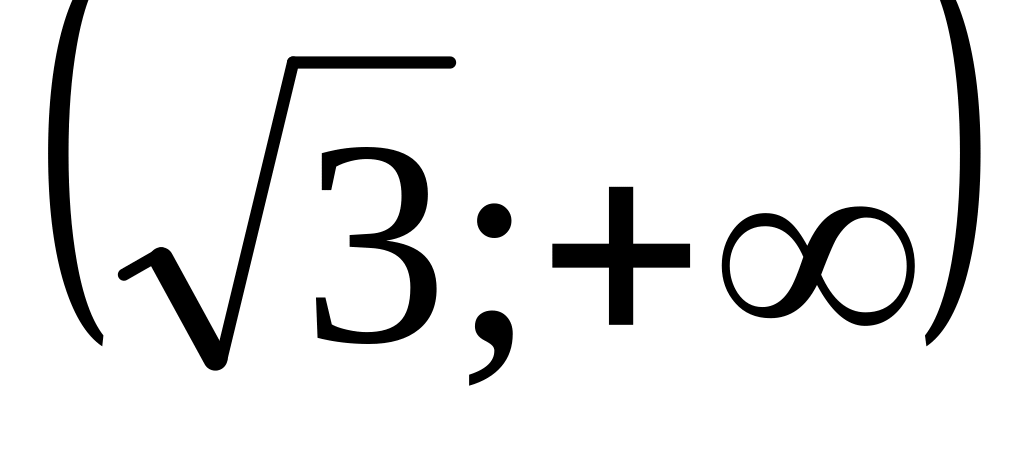
	+	Не существует	+	Не существует	+
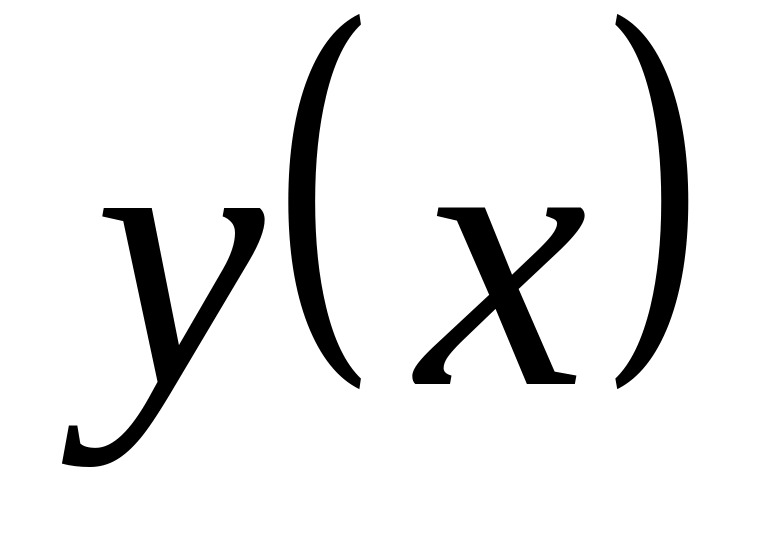
		Не существует		Не существует
	возрастает		возрастает		возрастает

7. Исследуем функцию на выпуклость и вогнутость, найдём точки перегиба:

.

Определим критические точки для второй производной:

, т.е. , откуда ;

не существует при .

Составим таблицу:

	+	Не существует	_		+	Не существует	_
		Не существует				Не существует
	вогнутая		выпуклая	Точка перегиба	вогнутая		выпуклая

8. Найдём значения функции в некоторых точках: , , , .

9. Построим график функции