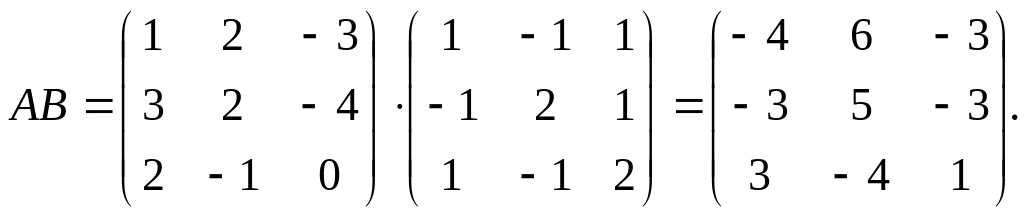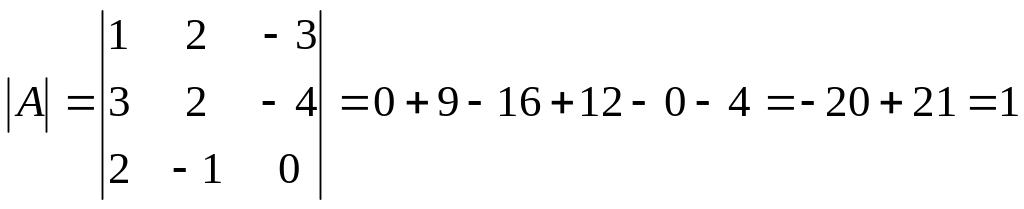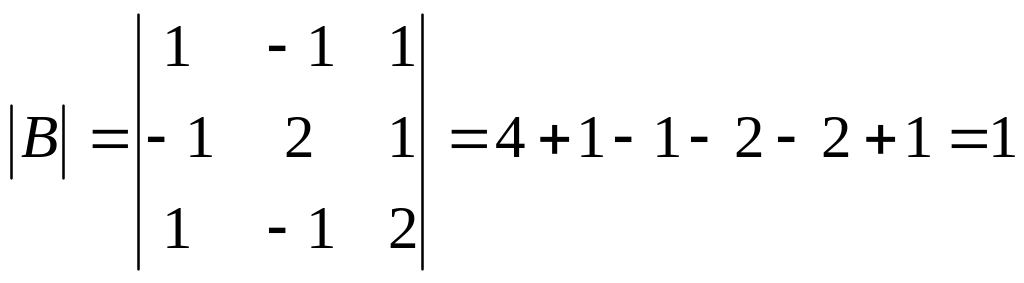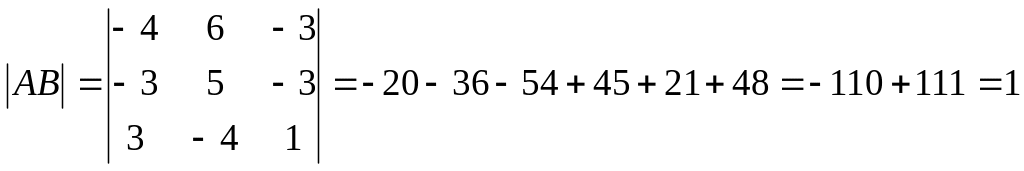Демонстрационный вариант контрольной работы № 1

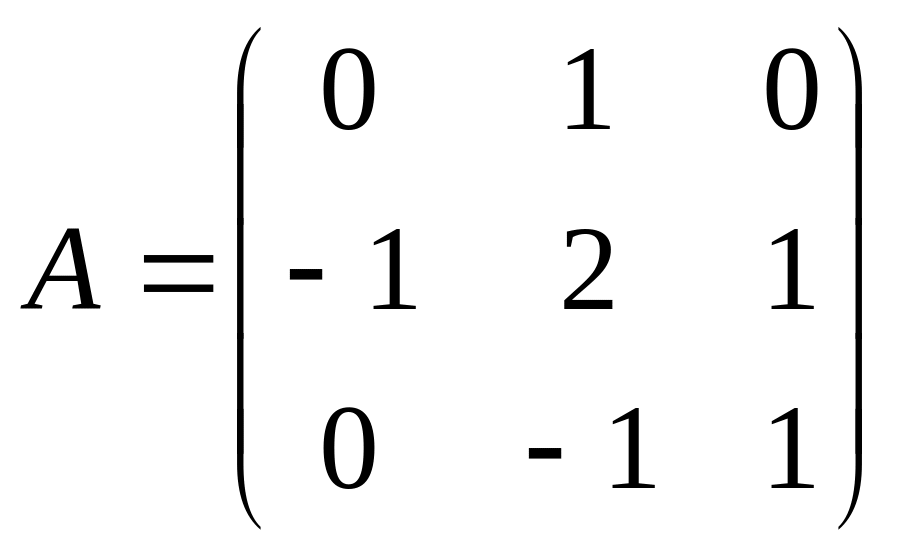1. Вычислить матрицу , где и .

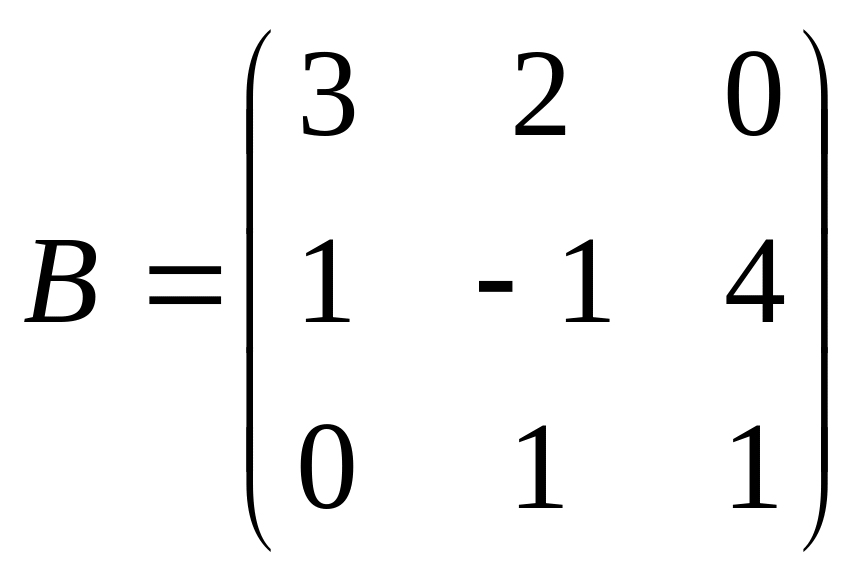2. Даны матрицы:

и 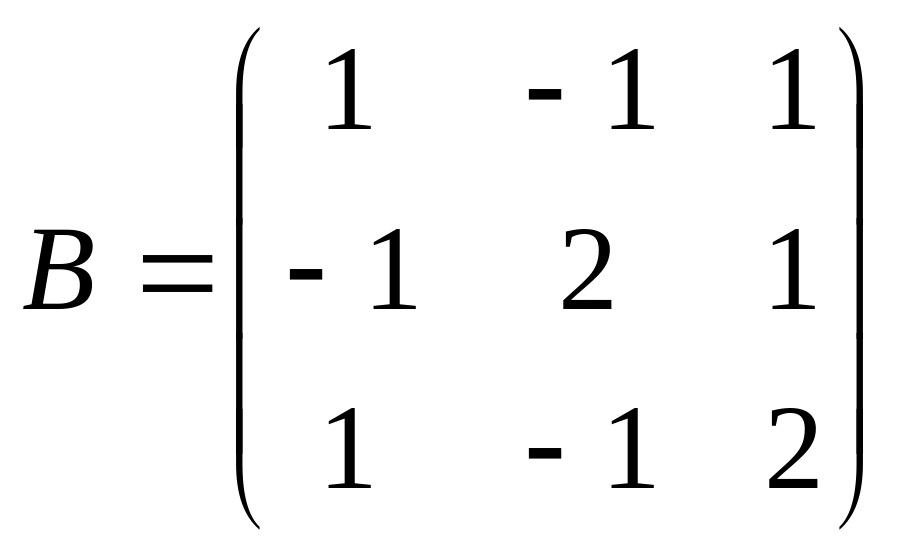. Найти произведение . Проверить на данном

примере, что определитель произведения матриц равен произведению их определителей.

3. Найти решение системы линейных уравнений: 1) методом Крамера; 2)методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.

4. Даны векторы (1;2;3) и (-1;3;2). Найти длины диагоналей и площадь параллелограмма, построенного на векторах 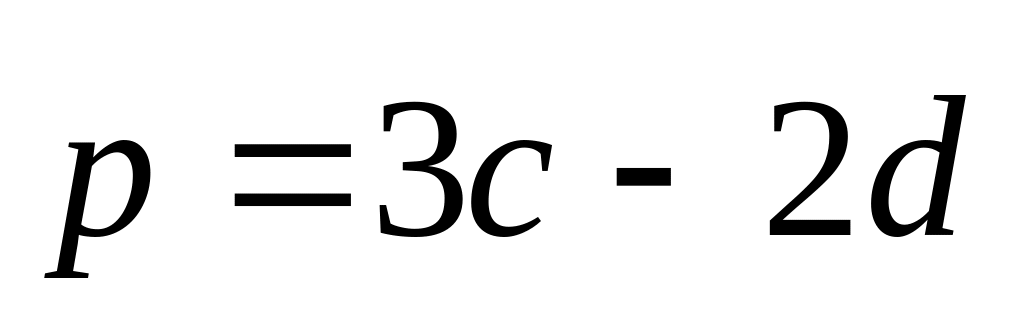и

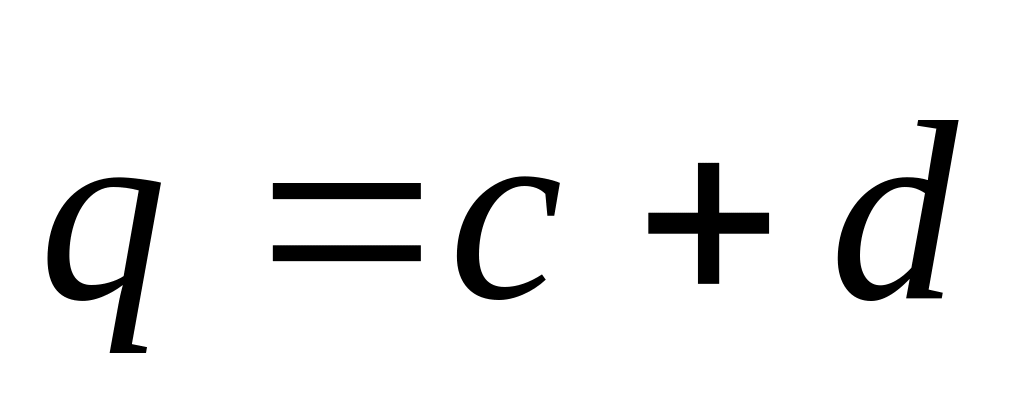
5. По координатам вершин пирамиды найти:

1) длины рёбер и ;

2) угол между рёбрами и ;

3) площадь грани ;

4) объём пирамиды;

5) уравнение плоскостей и .

.

4. Даны уравнения сторон треугольника х-3у+12=0 , 13х+2у-49=0 и 11х+8у+9=0. Написать уравнение медианы и высоты, проведенных на сторону 13х+2у-49=0 Сделать чертеж.

7. Построить графики функций: .

8. Вычислить пределы функций:

9. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.

10. Найти производные функций:

а) , б) , в)

11. Вычислить предел с помощью правила Лопиталя.

12. Провести полное исследование функции и построить её график.

Решение демонстрационного варианта контрольной работы №1 Решение задачи 1

1. вычислим :

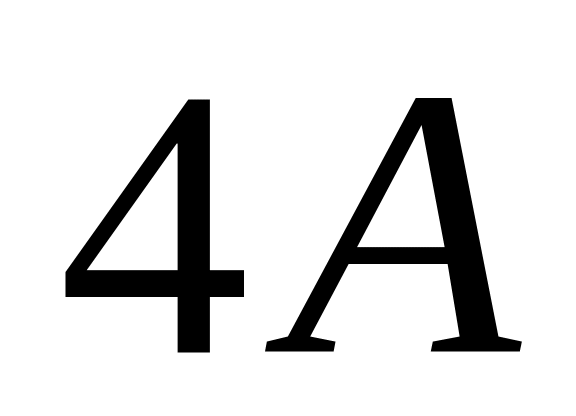4 =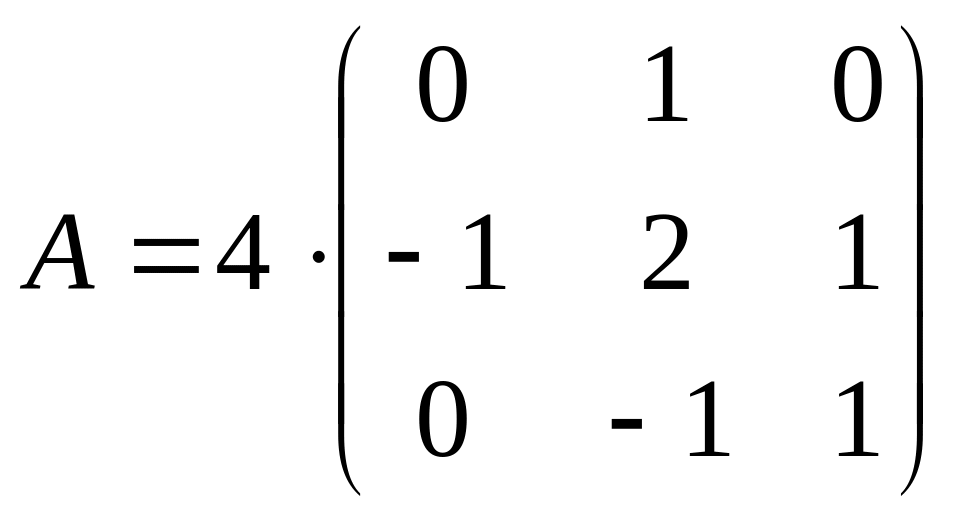

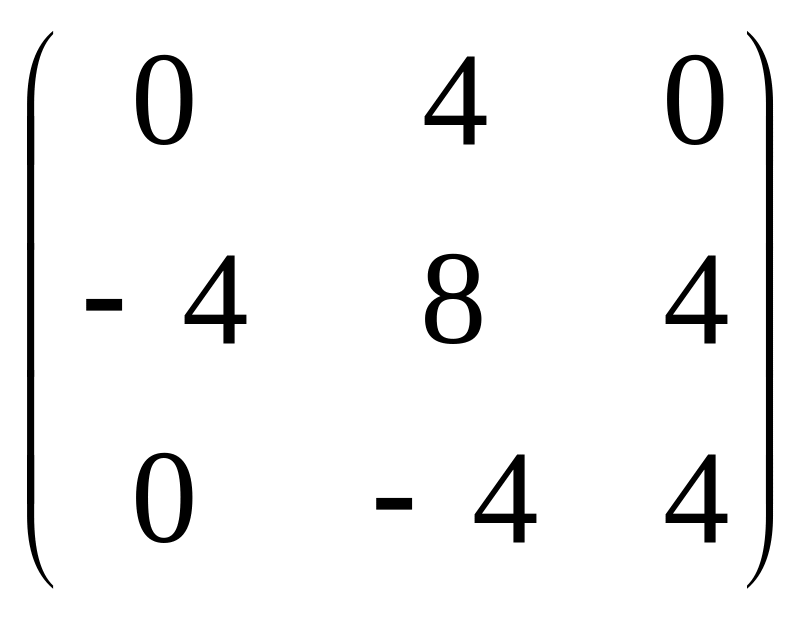
2. Найдём :

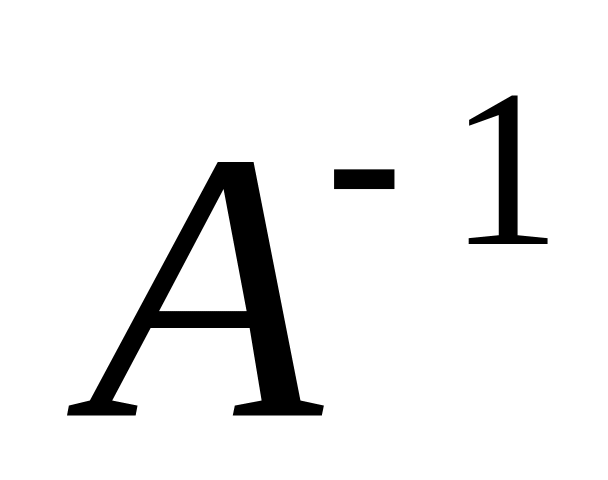Найдём определитель матрицы : , следовательно, обратная матрица существует.

Найдём алгебраические дополнения ко всем элементам матрицы .

Составим матрицу из этих алгебраических дополнений .

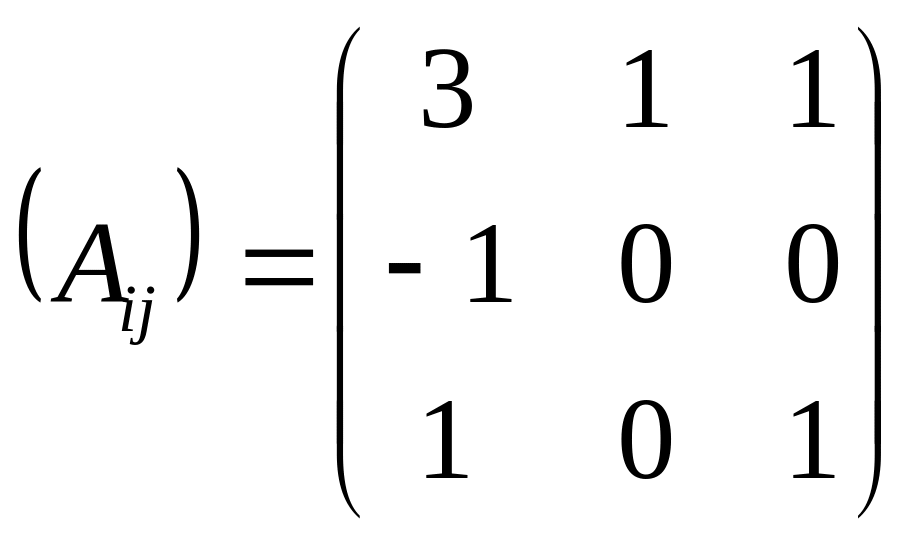Запишем матрицу . .

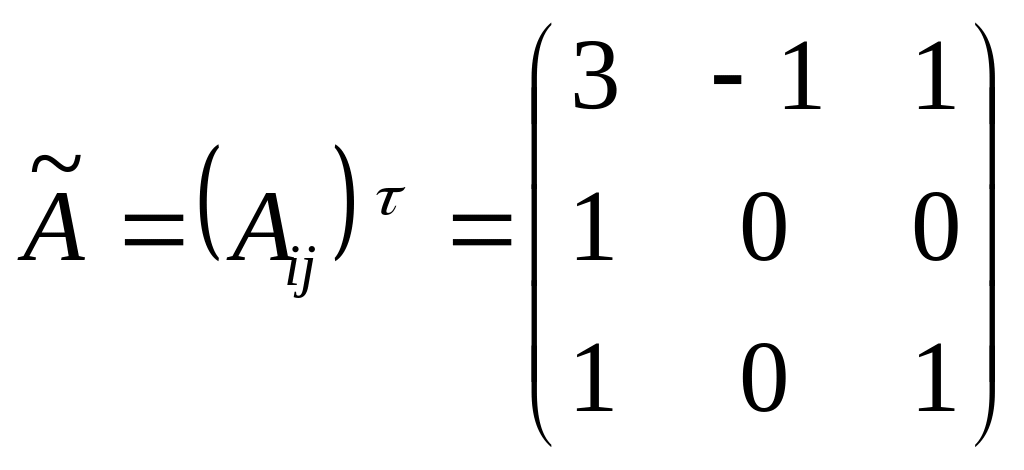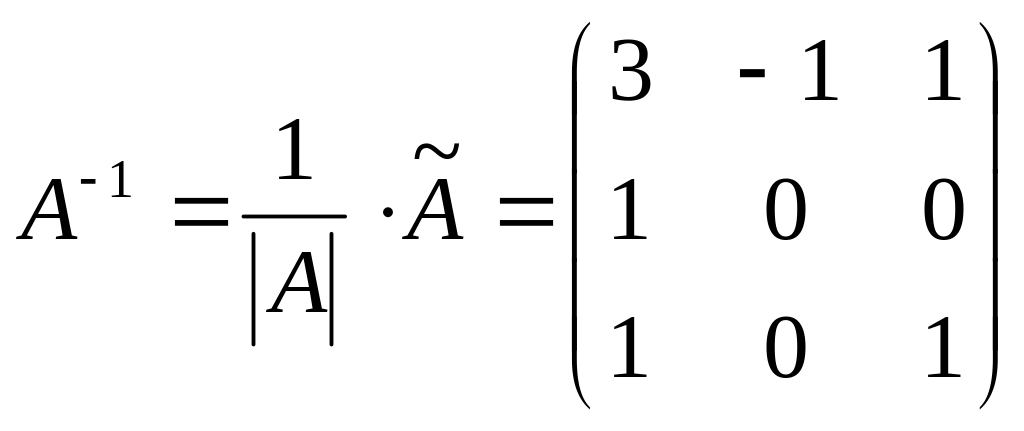3. Вычислим произведение

.

4. .

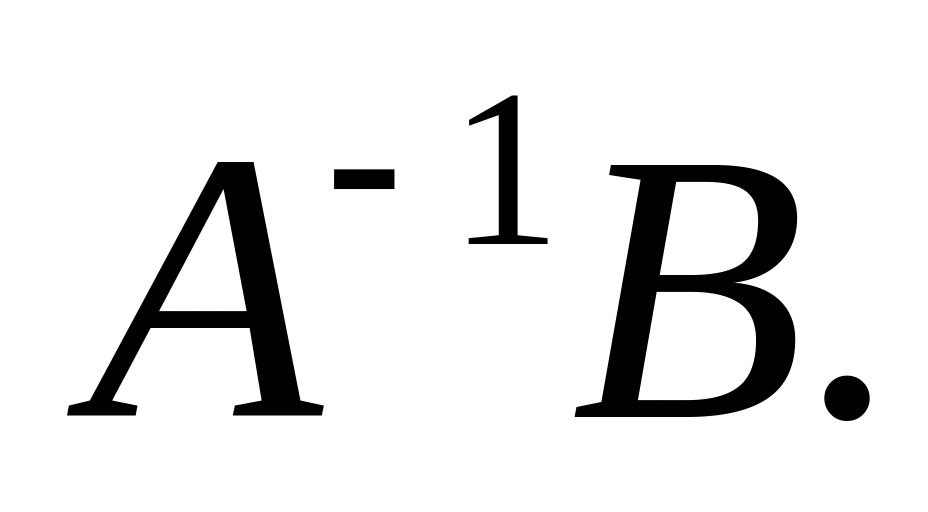
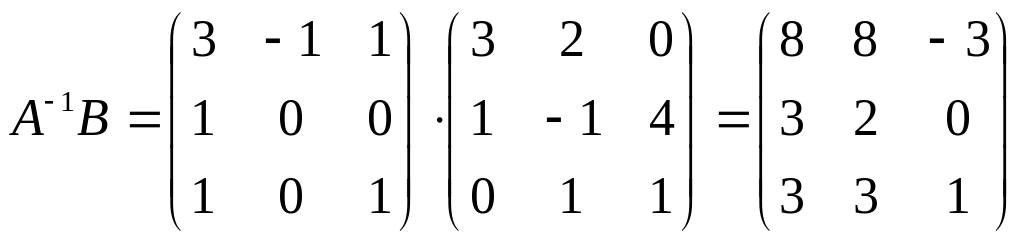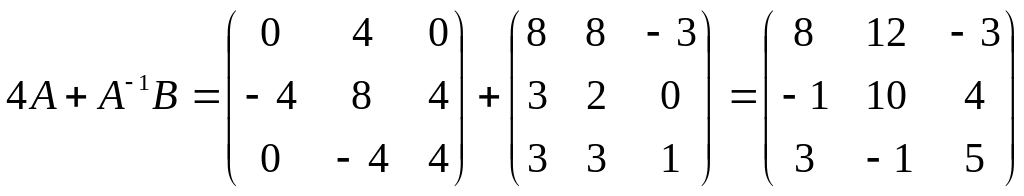Ответ: C= .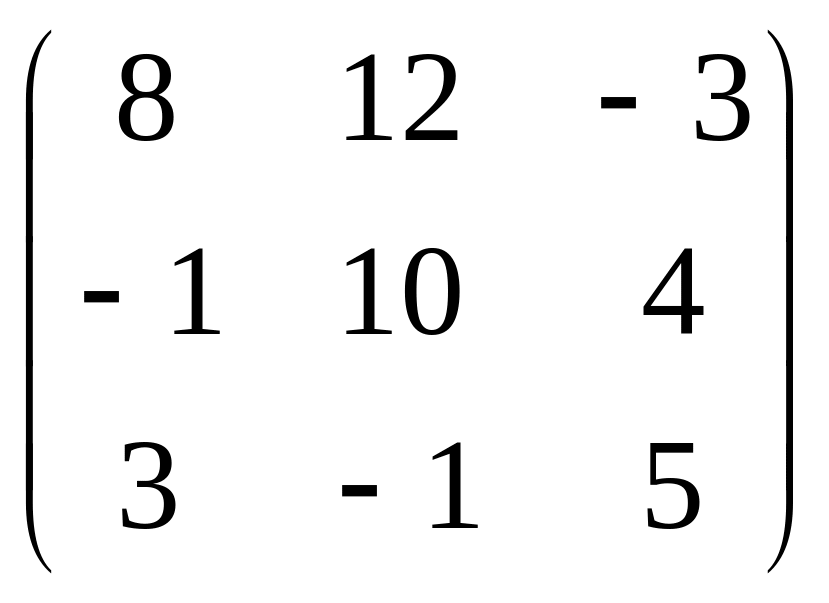

Решение задачи 2

1. 

2. 

3. 

4. 

Из 2)-4) следует, что , т.к. что и требовалось доказать.

Ответ: .

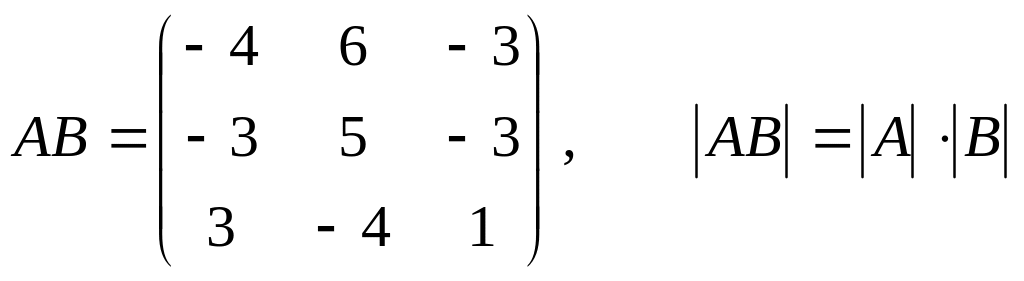Решение задачи 3

1. Метод Крамера

Вычислим определитель системы: .

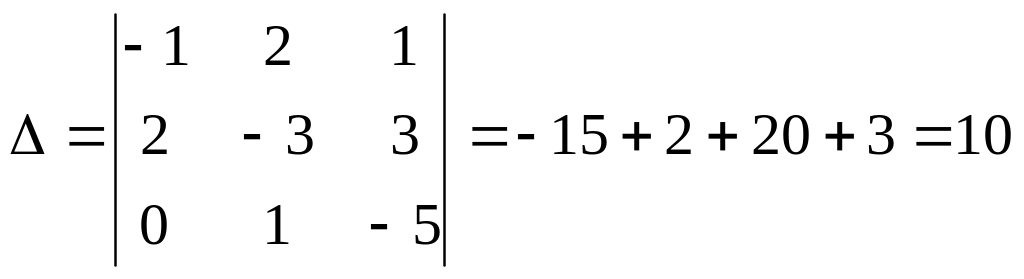Найдём :

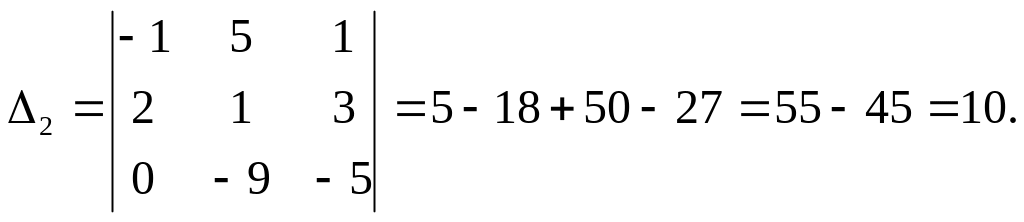
Проверка корней:

подставим полученные значения неизвестных в систему

Ответ: .

2. Метод обратной матрицы (матричный метод)

Запишем систему линейных уравнений в матричной форме: 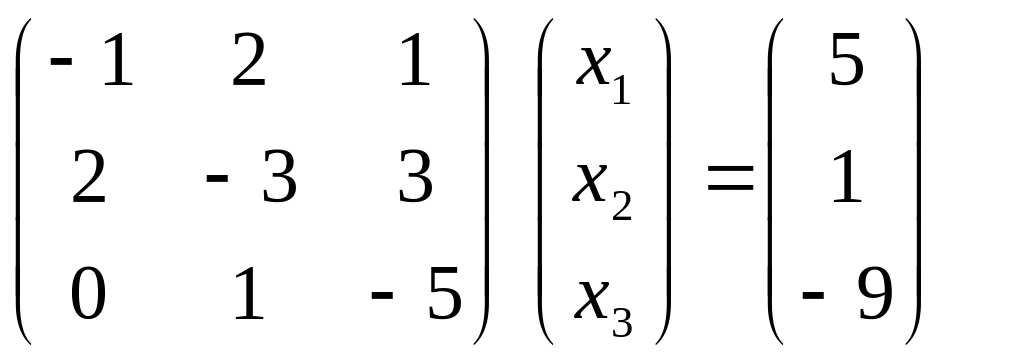; То есть АХ=В, умножая слева обе части уравнения на А^-1, получаем , где

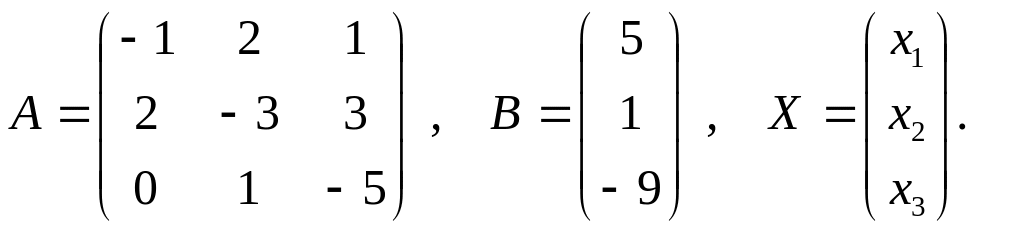
Так как определитель матрицы системы отличен от нуля: , то матрица имеет обратную. Для нахождения обратной матрицы вычислим алгебраические дополнения элементов матрицы .

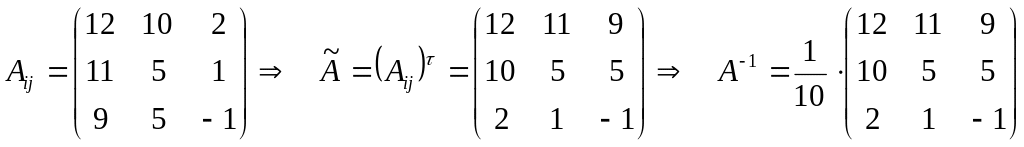
Правильность нахождения обратной матрицы проверим средствами матричного исчисления:

АА^-1=А^-1А=Е.

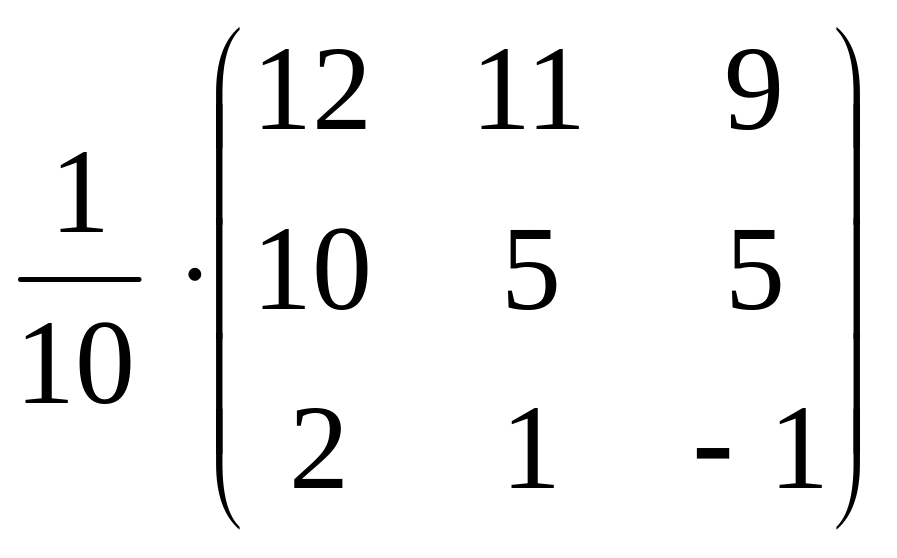= (Убедитесь в истинности этого равенства самостоятельно).

Матричное решение системы имеет вид

откуда следует (из условия равенства двух матриц), что

Ответ: .

3. Метод Гаусса

Составим расширенную матрицу и применим к ней преобразования:

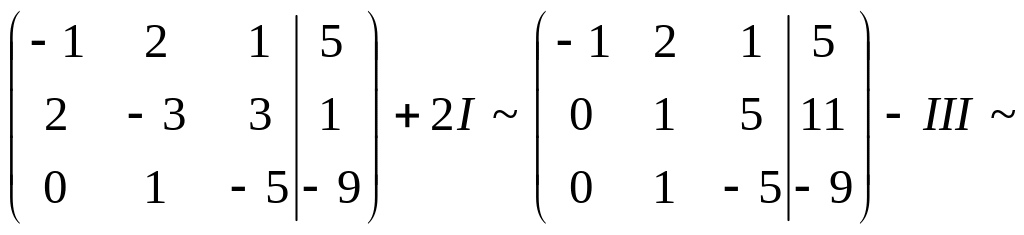
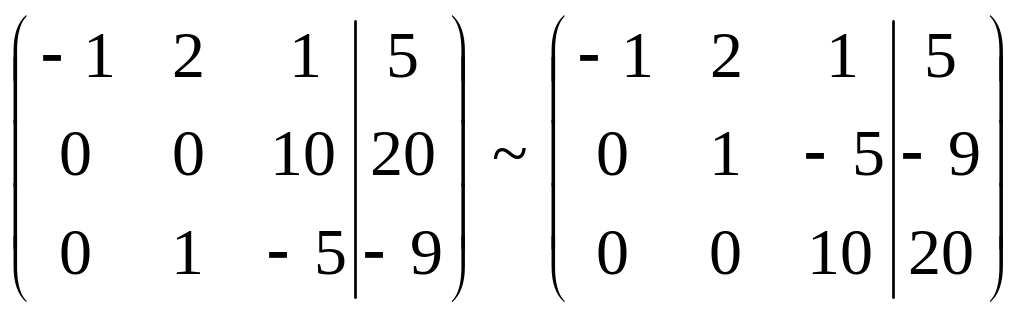
Итак, расширенная матрица с помощью элементарных преобразований сведена к ступенчатому виду. Перейдём к равносильной системе

отсюда

Ответ: