
- •Институт кафедра информатики и вычислительной техники
- •1. Введение
- •2. Цели и задачи контрольных работ
- •2. Требования к результатам контрольной работы
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Демонстрационный вариант контрольной работы № 1
- •Решение демонстрационного варианта контрольной работы №1 Решение задачи 1
- •Решение задачи 2
- •Решение задачи 3
- •Решение задачи 4 Запишем разложение по базису заданные вектора , . Используя свойства линейных операции, найдем разложение по базису искомых векторов
- •Решение задачи 5
- •Решение задачи 6
- •Решение задачи 7
- •Решение задачи 8
- •Решение задачи 9
- •Решение задачи 10
- •Решение задачи 11
- •Решение задачи 12
- •Контрольная работа №2
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Демонстрационный вариант контрольной работы №2
- •Решение демонстрационного варианта контрольной работы № 2 Решение задачи 1
- •Решение задачи 6
- •Решение задачи 7
- •Решение задачи 8
- •Решение задачи 9
- •Решение задачи 10
- •Решение задачи 11
- •Решение задачи 12
- •Контрольная работа № 1с
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •6. Выполнение и оформление контрольной работы
- •7. Учебно-методическое обеспечение а. Основная литература
- •Б. Дополнительная литература
- •В. Программное обеспечение
- •Г. Базы данных, информационно-справочные и поисковые системы
- •Математика Методические указания
- •610002 Киров, Казанская, 91
Контрольная работа № 1с
(только для студентов заочной формы, со сроком обучения 3 года)
Вариант 1
1.
Вычислить матрицу
![]() ,
где
и
.
,
где
и
.
2. Найти решение системы линейных уравнений методом Крамера, методом обратной матрицы, методом Гаусса.
![]()
3. По координатам вершин пирамиды найти:
длины рёбер и ;
угол между рёбрами и ;
площадь грани ;
объём пирамиды;
уравнение плоскостей и .
.
4. Вычислить пределы функций:
![]()
5. Найти производные функций:
а) , б) , в) .
6. Провести полное исследование функции и построить её график.
7. Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а,б,в) проверить дифференцированием. Найти определённый интеграл (г).
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
г)
.
г)
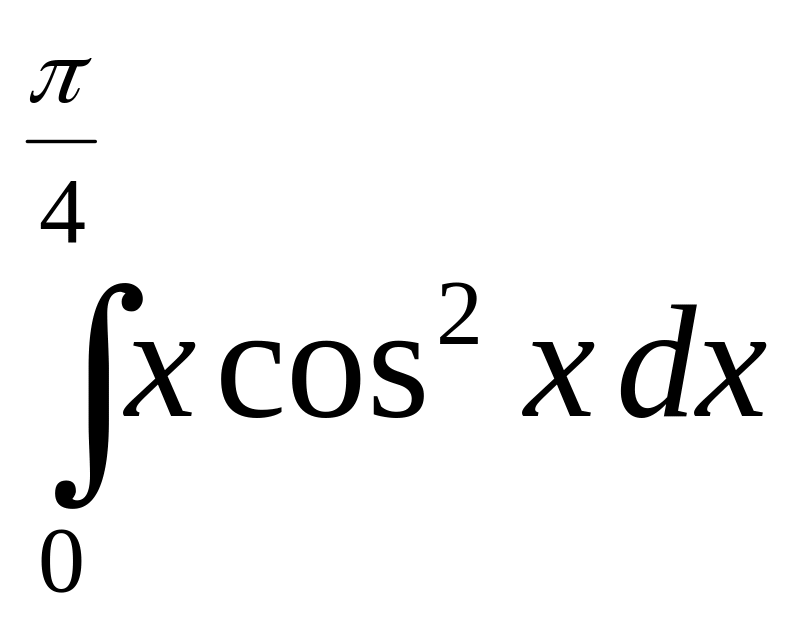
8. Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.
![]() .
.
9. Найти частные производные первого и второго порядка функций:
а)
![]() б)
б)
![]()
10.
Исследовать на экстремум функцию
![]() .
.
11. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее заданным начальным условиям:
![]() ;
;
![]() .
.
12. Найти радиус и интервал сходимости степенного ряда.
Исследовать сходимость ряда на концах интервала сходимости.
![]()
Вариант 2
1.
Вычислить матрицу
![]() ,
где
и
.
,
где
и
.
2. Найти решение системы линейных уравнений: методом Крамера, методом обратной матрицы, методом Гаусса.
![]()
3. По координатам вершин пирамиды найти:
длины рёбер и ;
угол между рёбрами и ;
площадь грани ;
объём пирамиды;
уравнение плоскостей и .
.
4. Вычислить пределы функций:
![]()
5. Найти производные функций:
а) , б) , в) .
6. Провести полное исследование функции и построить её график.
7. Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а,б,в) проверить дифференцированием. Найти определённый интеграл (г).
а)
![]() ,
б)
,
б)
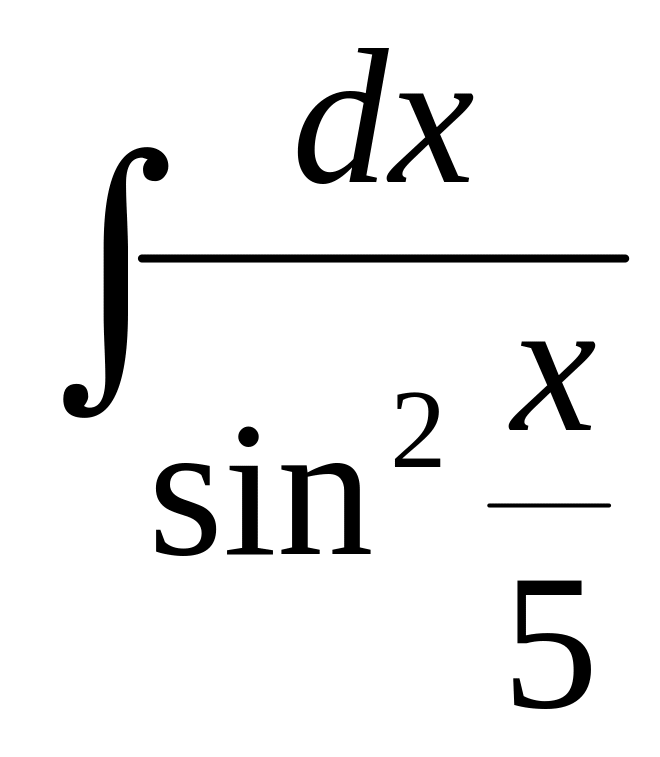 ,
в)
,
в)
![]() .
г)
.
г)
![]()
8. Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.
![]() .
.
9.Найти частные производные первого и второго порядка функций:
а)
![]() б)
б)
![]()
10.
Исследовать на экстремум функцию
![]() .
.
11. Найти общее решение дифференциального уравнения и частное решение,
удовлетворяющее заданным начальным условиям:
![]() ;
;
![]() .
.
12. Найти радиус и интервал сходимости степенного ряда.
Исследовать сходимость ряда на концах интервала сходимости.
![]()
Вариант 3
1. Вычислить матрицу , где и .
2. Найти решение системы линейных уравнений: методом Крамера, методом обратной матрицы, методом Гаусса.
![]()
3. По координатам вершин пирамиды : А1(-1;-2;1) А2(-2;-2;5) А3(-3;-1;1) А4(-1;0;3) найти:
длины рёбер и ;
угол между рёбрами и ;
площадь грани ;
объём пирамиды;
уравнение плоскостей и .
4. Вычислить пределы функций:
![]()
5. Найти производные функций:
а) , б) , в)
6. Провести полное исследование функции и построить её график: .
7. Найти интегралы. Правильность полученных результатов для неопределённых интегралов (а,б,в) проверить дифференцированием. Найти определённый интеграл (г).
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]()
8. Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.
![]()
9. Найти частные производные первого и второго порядка функций:
а)
![]() б)
б)
![]()
10.
Исследовать на экстремум функцию
![]() .
.
11.
Найти решение дифференциального
уравнения, удовлетворяющее указанным
начальным условиям:
![]() ;
;
![]() .
.
12.
Найти радиус, интервал и область
сходимости ряда:
![]() .
.
