ВЯТСКИЙ

СОЦИАЛЬНО-ЭКОНОМИЧЕСКИЙ

Институт кафедра информатики и вычислительной техники

Математика

Методические указания

по самостоятельной работе студентов

направления подготовки 38.03.02 (080200.62) Менеджмент

степень выпускника: бакалавр

Киров

2014

Рассмотрено на заседании кафедры информатики и вычислительной техники, протокол № 1 от 9 сентября 2014 г.

Утверждено на заседании учебно-методического совета, протокол № 87 от 20 октября 2014 г.

Математика: Методические указания / Сост. А.И. Глушкова. – Киров: ВСЭИ, 2014. – 60 с.

Методические указания разработаны в соответствии с учебной программой дисциплины и предназначены для студентов, обучающихся по направлению подготовки 38.03.03 (080200.62) Менеджмент (степень выпускника: бакалавр)

© Вятский социально-экономический

институт (ВСЭИ), 2014

1. Введение

Самостоятельная работа студентов по курсу включает в себя:

- для студентов, обучающихся по заочной форме обучения, на базе среднего (полного) общего образования), срок обучения 5 лет – две контрольные работы (№ 1, № 2);

- для студентов, обучающихся по заочной форме обучения, на базе среднего профессионального или высшего профессионального образования, срок обучения 3 года – одну контрольную работу (№ 1с).

2. Цели и задачи контрольных работ

Цель контрольной работы: изучение основных понятий высшей математики: линейной алгебры, аналитической геометрии, математического анализа.

Задачи контрольной работы:

1. Формирование основных приемов решения практических задач по темам дисциплины.

2. Формирование практических навыков использования математического материала в исследовательской и профессиональной деятельности.

3. Формирование у студентов умений строить стандартные теоретические и экономические модели, анализировать и содержательно интерпретировать полученные результаты, используя аппарат линейной алгебры и математического анализа.

2. Требования к результатам контрольной работы

В результате выполнения контрольной работы студент должен:

Знать:

- методы линейной алгебры и аналитической геометрии;

- методы дифференциального и интегрального исчислений;

- функцию нескольких переменных;

- ряды и их сходимость, разложение элементарных функций в ряд;

- методы решения дифференциальных уравнений 1 и 2 порядка.

Уметь:

- применять математические методы для решения практических задач;

- исследовать функции, строить их графики;

- вычислять производные и интегралы, в том числе для ФНП;

- исследовать ряды на сходимость;

- решать дифференциальные уравнения.

Владеть:

- навыками решения задач линейной алгебры и аналитической геометрии;

- аппаратом дифференциального и интегрального исчислений функции одного и

нескольких переменных;

- навыками исследования числовых и функциональных рядов на сходимость;

- навыками решения дифференциальных уравнений 1 и 2 порядка.

3. Объем самостоятельной работы студента

Самостоятельная работа студента составляет 3,5 зачетные единицы по очной форме обучения, 6 зачетных единиц по заочной форме обучения.

Выполнение контрольной работы предполагает самостоятельную работу студента по всем разделам учебной программы.

5. Варианты контрольной работы

Контрольная работа №1

(только для студентов заочной формы, со сроком обучения 5 лет)

Вариант 1

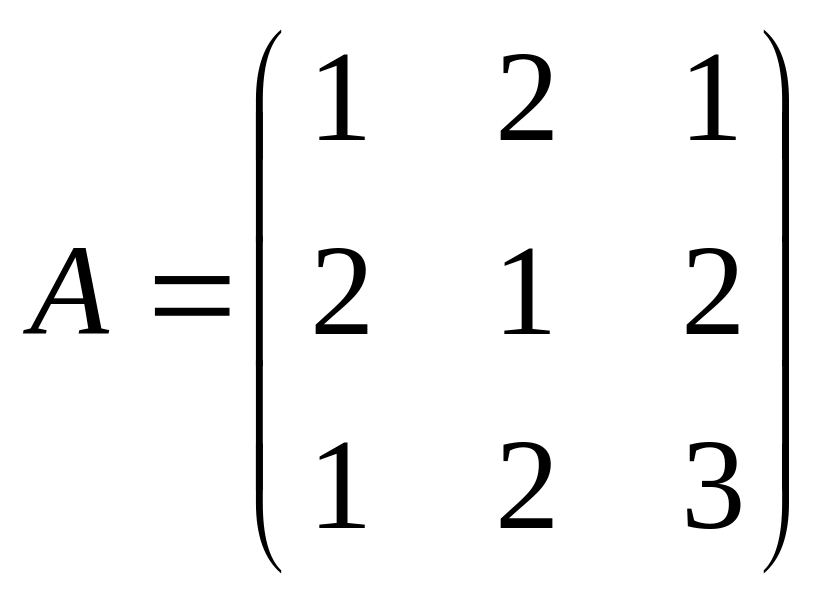1. Вычислить матрицу , где и .

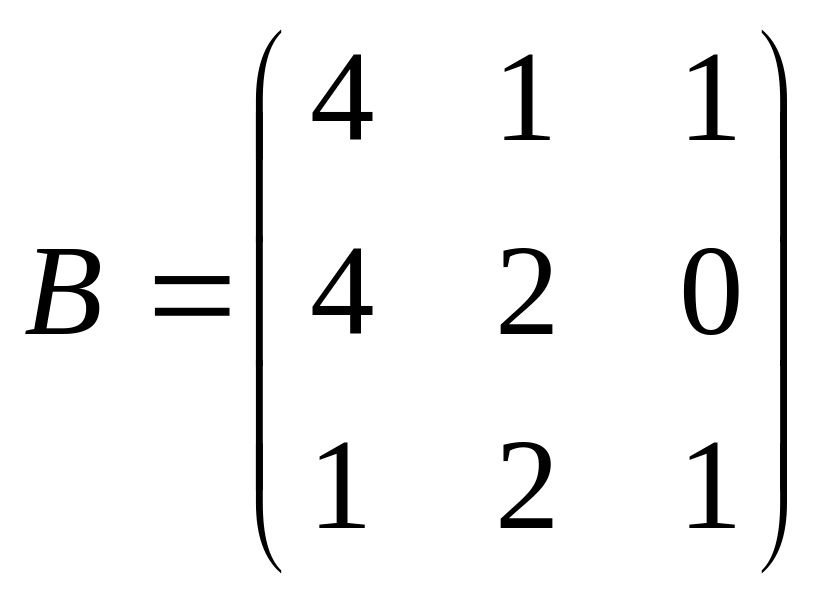2. Даны матрицы:

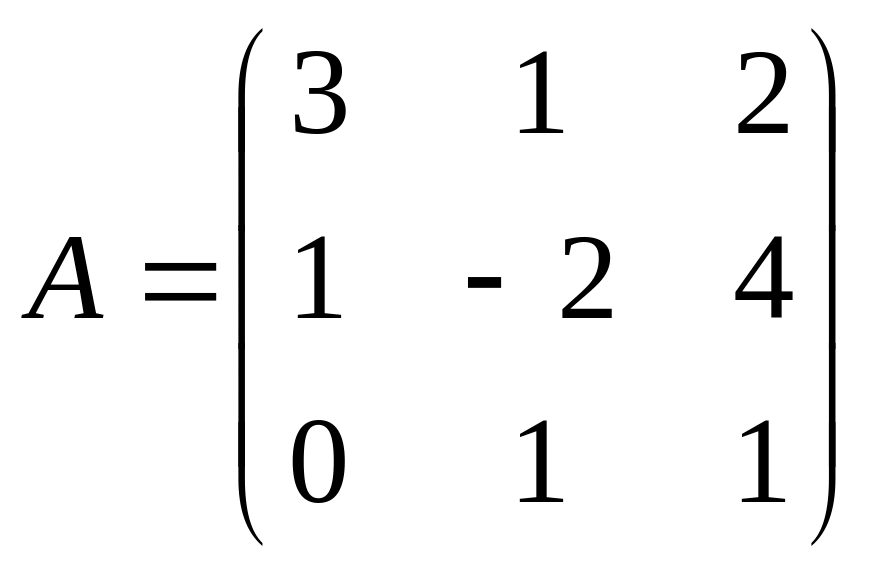и 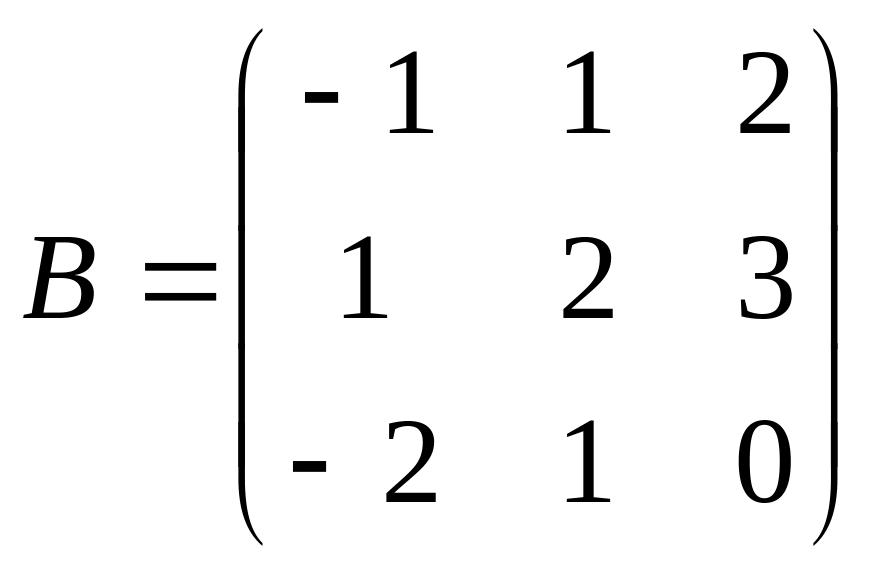. Найти произведение . Проверить на данном

примере, что определитель произведения матриц равен произведению их определителей.

3. Найти решение системы линейных уравнений: 1) методом Крамера; 2)методом Гаусса; 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.

4. Даны векторы (0;1;-1) и (1;1;-4). Найти длины диагоналей и площадь параллелограмма, построенного на векторах и

5. По координатам вершин пирамиды найти:

1. длины рёбер 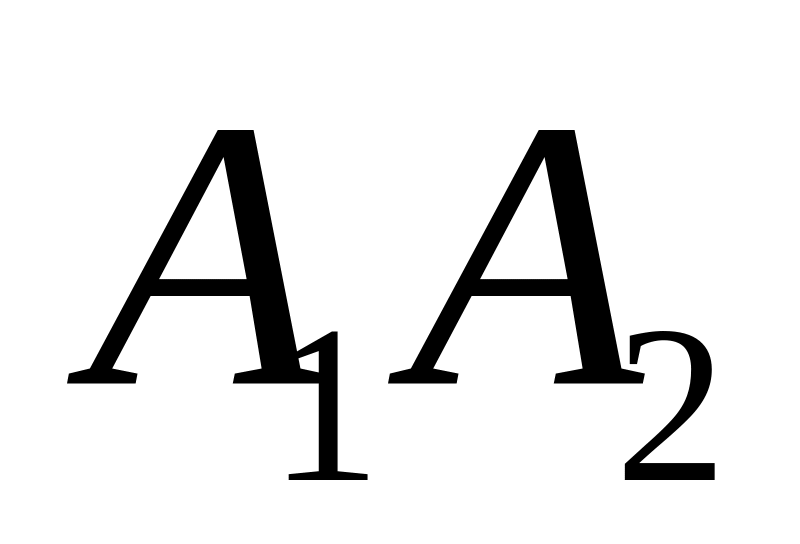и ;

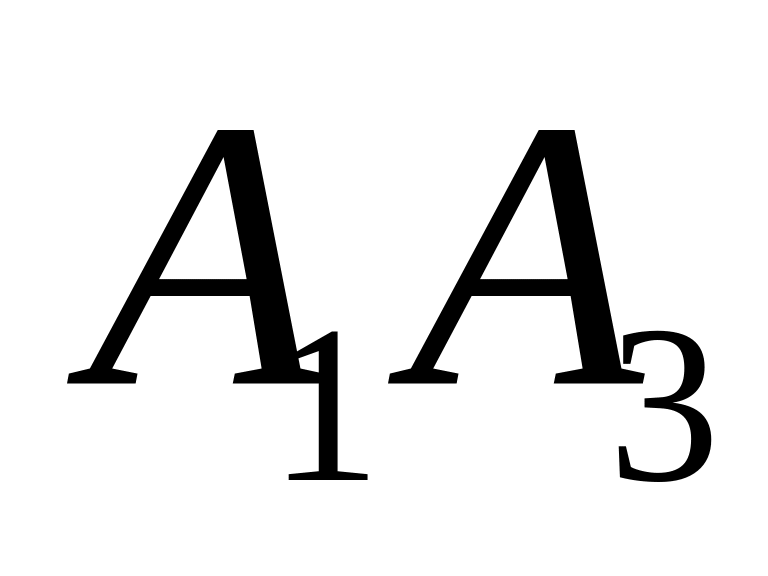2. угол между рёбрами и ;

3. площадь грани ;

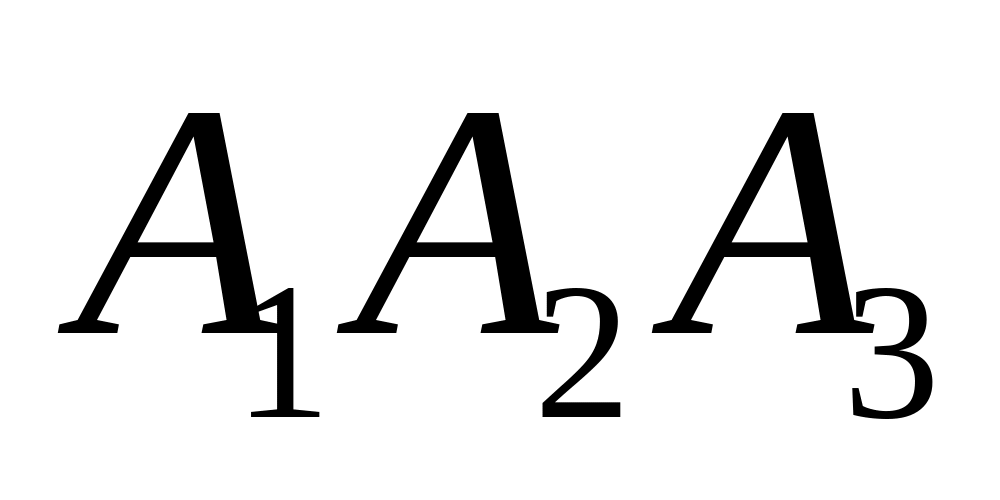4. объём пирамиды;

5. уравнение плоскостей и .

.

6. Даны уравнения сторон треугольника 2х-5у=3, х+3у=7 и 3х-2у+1=0.Написать уравнение медианы и высоты, проведенных на сторону 2х-5у=3. Сделать чертеж.

7. Построить графики функций: .

8. Вычислить пределы функций:

9. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.

10. Найти производные функций:.

а) , б) , в) .

11. Вычислить предел с помощью правила Лопиталя.

12. Провести полное исследование функции и построить её график.