21. Даны точки: . Вычислить:
а) Скалярное произведение векторов , , а также косинус угла между ними.
б) Векторное произведение векторов , , площадь образуемой ими грани и синус угла между ними. Последний проверить с помощью основного тригонометрического тождества.
в) Смешанное произведение векторов , , (как непосредственно, так и используя найденное векторное произведение), объём пирамиды ABCD и её высоту, опущенную на грань векторов , .
22. Даны точки: . Вычислить:
а) Скалярное произведение векторов , , а также косинус угла между ними.
б) Векторное произведение векторов , , площадь образуемой ими грани и синус угла между ними. Последний проверить с помощью основного тригонометрического тождества.
в) Смешанное произведение векторов , , (как непосредственно, так и используя найденное векторное произведение), объём пирамиды ABCD и её высоту, опущенную на грань векторов , .
23. На векторах построен параллелепипед. Вычислить:
а) Скалярное произведение векторов , , а также косинус угла между ними.
б) Векторное произведение векторов , , площадь образуемой ими грани и синус угла между ними. Последний проверить с помощью основного тригонометрического тождества.
в) Смешанное произведение векторов , , (как непосредственно, так и используя найденное векторное произведение), объём параллелепипеда и его высоту, опущенную на грань векторов .
24. Даны точки: . Вычислить:
а) Скалярное произведение векторов , , а также косинус угла между ними.
б) Векторное произведение векторов , , площадь образуемой ими грани и синус угла между ними. Последний проверить с помощью основного тригонометрического тождества.
в) Смешанное произведение векторов , , (как непосредственно, так и используя найденное векторное произведение), объём пирамиды ABCD и её высоту, опущенную на грань векторов , .
25. Даны точки: . Вычислить:
а) Скалярное произведение векторов , , а также косинус угла между ними.
б) Векторное произведение векторов , , площадь образуемой ими грани и синус угла между ними. Последний проверить с помощью основного тригонометрического тождества.
в) Смешанное произведение векторов , , (как непосредственно, так и используя найденное векторное произведение), объём пирамиды ABCD и её высоту, опущенную на грань векторов , .
II.
1. Составить
общее уравнение плоскости, проходящей
через точку
и прямую
, а также найти расстояние между ними.
2. Составить
общее уравнение плоскости, проходящей
через точку
и прямую
,
а также найти расстояние между ними.
3. Составить
общее уравнение плоскости, проходящей
через прямую
,
где
,
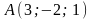и параллельной прямой
,
,
а также найти расстояние между этими
прямым.
4. Составить
общее уравнение плоскости, проходящей
через прямую
и параллельной прямой
, а также найти расстояние между этими
прямым.
5. Составить
общее уравнение плоскости, проходящей
через точку
и прямую
.
Найти расстояние от точки
до этой прямой.
6. Составить
общее уравнение плоскости, проходящей
через прямые:
и
, а также найти расстояние между этими
прямым.
7. Составить
общее уравнение плоскости, проходящей
через точку
и прямую
,
.
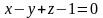Найти расстояние от точки М
до этой прямой.
8. Составить
общее уравнение плоскости, проходящей
через прямую
и параллельной прямой
, а также найти расстояние между этими
прямым.
9. Составить
общее уравнение плоскости, проходящей
через точку
и прямую
,
а также найти рсстояние между ними.
10. Составить
общее уравнение плоскости, проходящей
через прямую
и параллельной прямой (
,
),
а также найти расстояние между этими
прямым.
11. Составить
общее уравнение плоскости, проходящей
через точку
и прямую
.
Найти расстояние от этой плоскости до
параллельной ей плоскости
.
12. Найти
угол между прямой (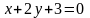
,
)
и плоскостью
,
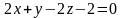а также координаты точки их пересечения.
13. Составить
общее уравнение плоскости, проходящей
через точки
,
,
,
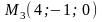а также расстояние от M1
до прямой (M2M3).
14. Составить
общее уравнение плоскости, проходящей
через точки
,
,
.
Найти расстояние от этой плоскости до
плоскости
.
15. Составить
общее уравнение плоскости, проходящей
через прямые
и
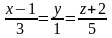, а также найти расстояние между этими
прямым.
16. Составить
общее уравнение плоскости, проходящей
через прямую
и параллельной прямой
, а также найти расстояние между этими
прямым.
17. Составить
общее уравнение плоскости, проходящей
через прямую
,
где
,
,
перпендикулярно плоскости
.
Найти угол между этой плоскостью и
плоскостью
.
18. Найти
расстояние между прямым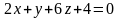и: (
,
)
и
.
Показать, что они лежат в одной плоскости
и получить её общее уравнение.
19. Составить
общее уравнение плоскости, проходящей
через прямую
,
,
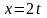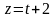и параллльной прямой
,
,
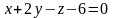а также найти расстояние между этими
прямым.
20.
Найти расстояние от точки
до прямой (
,
)
и общее уравнение проходящей через них
плоскости.
21. Найти
общие уравнения проекции прямой
на плоскость
и координаты точки их пересечения.
22. Составить
общее уравнение плоскости, проходящей
через прямую
и параллельной прямой
,
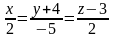а также найти расстояние между этими
прямым.
23. Составить
общее уравнение плоскости, проходящей
через точку
и прямую
,
а также найти расстояние между этими
точкой и прямой.
24. Составить
общее уравнение плоскости, проходящей
через прямые
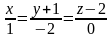и
,
а также найти расстояние между этими
прямым.
25. Составить
общее уравнение плоскости, проходящей
через точку
перпендикулярно прямой (
,
).
Найти расстояние от точки
до этой прямой.