Розділ 7. Класична центральна гранична теорема

7.1. Центральна гранична теорема (цгт)

7.1.1. Постановка задачі. Умова Ліндеберга, її ймовірнісний зміст. До ЦГТ відносяться твердження, у яких іде мова про збіжність розподілів сум до нормального закону. Нехай маємо послідовність випадкових величин . Якщо існують послідовності дійсних чисел і такі, що функція розподілу суми збігається до функції розподілу стандартного нормального закону при , то кажуть, що для послідовності має місце ЦГТ. В цьому випадку говорять, що випадкова величина асимптотично нормальна з параметрами і . Асимптотична нормальність відіграє важливу роль в теорії і на практиці, вона дозволяє замінити складні розподіли сум добре вивченим нормальним розподілом. ЦГТ є підставою для широкого використання нормального закону в статистиці.

Нехай задана послідовність незалежних випадкових величин із скінченними математичними сподіваннями , скінченними дисперсіями і функціями розподілу . Позначимо через і нехай для довільного

.

Якщо для довільного

, (1)

то (1) називають умовою Ліндеберга.

Вияснимо ймовірнісний зміст умови Ліндеберга, для цього розглянемо події , , і подію

.

Тоді , а

.

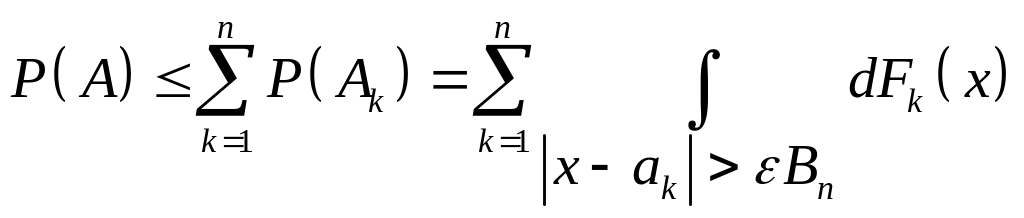Якщо врахуємо, що в області інтегрування , то одержимо

. (2)

Якщо виконується умова Ліндеберга, то із (2) випливає, що

.

Тобто, якщо виконується умова Ліндеберга, то випадкові величини будуть рівномірно нескінченно малі.

7.1.2. Теорема Ліндеберга. Будемо використовувати позначення, що введені в попередньому пункті. Крім того, позначимо , – функція розподілу випадкової величини , а – функція розподілу стандартного нормального закону.

Теорема 1. Нехай задана послідовність незалежних випадкових величин із скінченними математичними сподіваннями і скінченними дисперсіями . Якщо для довільного виконується умова Ліндеберга (1), то рівномірно відносно

. (3)

Доведення. Позначимо , – функцію розподілу . Тоді , , , , .

В цих позначеннях , після виконання в інтегралі заміни , набуває вигляду:

. (4)

Нехай , тоді характеристична функція

.

Покажемо, що при рівномірно відносно прямують до одиниці. Врахувавши, що , одержимо

.

Із нерівності (Н1) із попереднього розділу при для довільного дійсного

,

тому із (4) для будь-якого додатного

, (5)

а при

. (6)

Отже, із умови Ліндеберга (1) випливає, що

і при всіх досить великих і

. (7)

Це означає, що не перетворюється в 0, тому при можна логарифмувати:

.

Щоб довести (3), на основі теореми про неперервну відповідність між збіжністю функцій розподілу і відповідних характеристичних функцій, нам треба довести, що

,

а для цього достатньо довести, що

. (8)

Використовуючи розклад , при одержимо . Звідки, при

, (9)

де .

Із (7) і (9) випливає справедливість рівності

.

Тоді

, (10)

де .

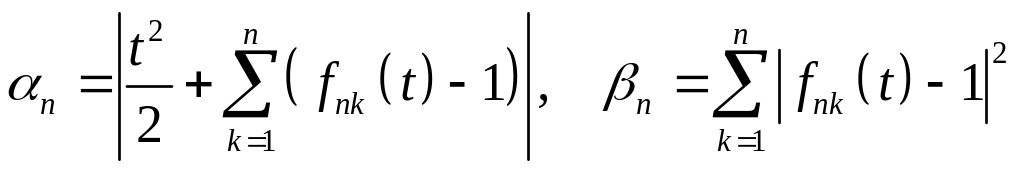Із (5) випливає, що , а оскільки , то звідси одержуємо наступну нерівність

.

Тому із (6) випливає, що при всіх досить великих і

. (11)

Переходимо до оцінки :

.

У першому інтегралі використаємо нерівність (Н1) , а у другому – (Н2) , тоді

.

Врахувавши, що , в кожному скінченному проміжку

. (12)