6.3. Збіжність в основному послідовності функцій розподілу. Теореми Хеллі. Слабка збіжність послідовності функцій розподілу

Будемо розглядати множину всіх функцій розподілу, а також множину узагальнених функцій розподілу , які неспадні на , неперервні зліва і . Узагальнена функція розподілу буде функцією розподілу тоді і тільки тоді, коли , .

Означення. Нехай , – узагальнені функції розподілу. Послідовність називається збіжною в основному до функції , якщо для будь-якої точки неперервності функції .

Відзначимо, що якщо послідовність функцій розподілу збігається в основному до функції , то функція може і не бути функцією розподілу. Наприклад, якщо то для всіх .

Множина називається всюди щільною в , якщо для довільного і для довільного існує таке, що .

Теорема 1. Нехай – довільна всюди щільна в множина, , – узагальнені функції розподілу. Якщо для довільного , то збігається в основному до . Якщо для всіх існує , то для деякої узагальненої функції розподілу послідовність збігається в основному до .

Доведення. Нехай будь-яка точка неперервності функції , і – будь-які точки із . Для довільного , тому при переході в нерівності до границі, коли , одержимо або . У цій нерівності перейдемо до границі, коли , а , тоді . Оскільки – точка неперервності , тобто , то із попередньої нерівності випливає, що існує .

Для доведення другої частини теореми для будь-якого покладемо , де , . Оскільки – неспадні, то і є неспадною на . Із визначення випливає, що і буде неспадною. Із монотонності одержуємо . Отже є узагальненою функцією розподілу. Нехай – точка неперервності .Для довільних дійсних і таких, що існують і і . Тоді . Якщо в цих нерівностях перейдемо до границі, коли і , то одержимо .

Теорема 2 (1-ша теорема Хеллі). Із будь-якої послідовності функцій розподілу можна вибрати підпослідовність , яка збігається в основному до деякої узагальненої функції розподілу .

Доведення. Нехай – зліченна всюди щільна в множина. Розглянемо послідовність . Оскільки вона обмежена, то вона містить збіжну підпослідовність . Її границю позначимо .

Розглянемо послідовність і покладемо . Дістанемо знову обмежену числову послідовність . Із неї знову можна виділити збіжну підпослідовність . Її границю позначимо . Продовжуючи цей процес, ми для кожної точки одержимо підпослідовність , яка в кожній із точок , буде збігатися до . На основі цих підпослідовностей побудуємо нову підпослідовність . Так побудована підпослідовність буде збігатися в кожній точці множини до функції .

Покладемо , тоді за теоремою 1 побудована підпослідовність буде збігатися в основному до функції .

Теорема 3 (2-га теорема Хеллі). Нехай послідовність функцій розподілу збігається в основному до функції розподілу ( , ). Тоді для довільної неперервної і обмеженої на функції

. (22)

Доведення. Розглянемо довільний скінченний проміжок , де і – точки неперервності . Із неперервності функції на відрізку випливає, що для довільного ми можемо вибрати таке розбиття проміжку точками , де – точки неперервності , що для всіх виконується нерівність

, (23)

де функція при .

Розглянемо нерівність

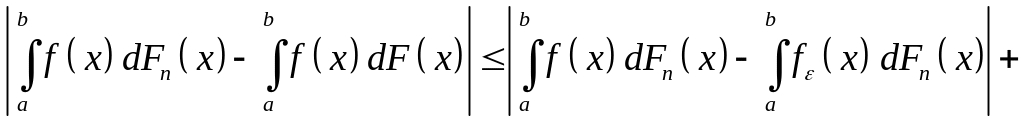
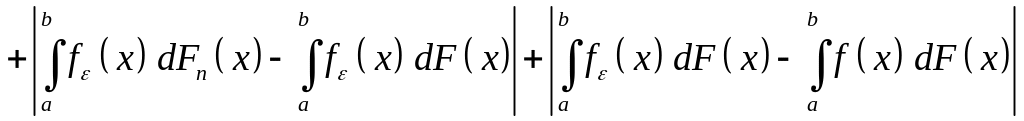. (24)

Із (23) і умови теореми одержуємо

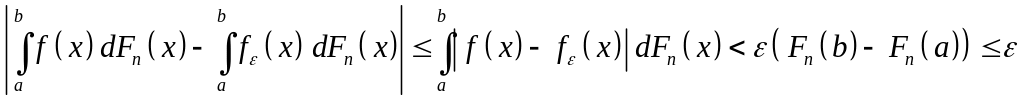, (25)

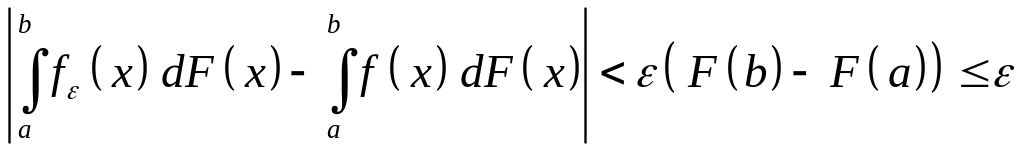. (26)

Другий доданок правої частини (24) зобразимо у вигляді

.

Функція обмежена, тому існує , що . Тому будемо мати

.

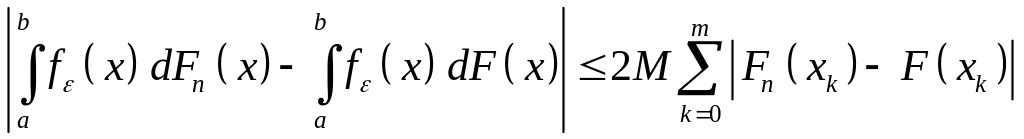Послідовність збігається в основному до , а - точки неперервності функції і цих точок скінченна кількість, тому для заданого існує , що для всіх буде виконуватись нерівність для всіх . Отже,

. (27)

Таким чином, із (24) – (27) випливає, що для довільного існує , що для всіх буде виконуватись нерівність 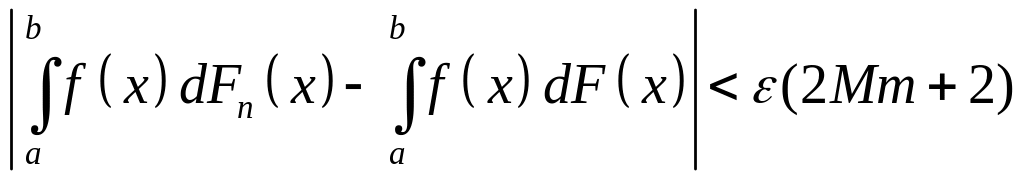, а це означає, що для довільного скінченного проміжоку

. (28)

Перейдемо до доведення (22). Для довільного виберемо і так, щоб і були точками неперервності і . Тоді існує , що для всіх . Зафіксуємо такі і .

.

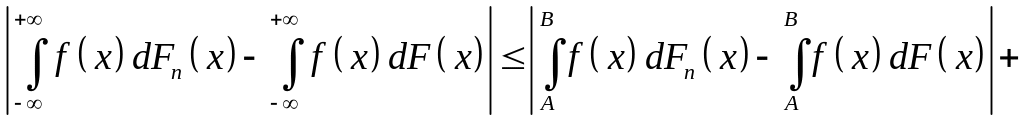
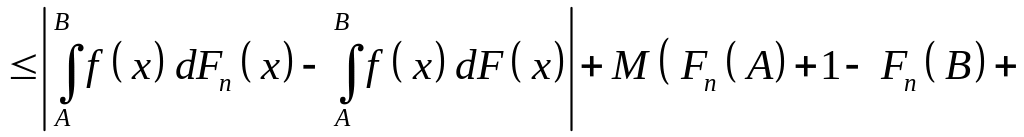
Із (28) випливає, що і перший доданок в правій частині вибором може бути як завгодно малим, тому із умов теореми одержуємо (22).

Означення. Нехай , і є функціями розподілу. Якщо для довільної неперервної і обмеженої на функції , то кажуть, що послідовність слабко збігається до (позначають або ).

Теорема 4. Для того, щоб послідовність функцій розподілу слабко збігалась до функції розподілу , необхідно і достатньо, щоб збігалась в основному до .

Доведення. Із теореми 3 випливає, що із збіжності в основному випливає слабка збіжність. Нехай має місце слабка збіжність. Тобто, для довільної неперервної і обмеженої на функції .

Виберемо функцію у вигляді:

Тоді

і

.

А тепер виберемо

Тоді

.

Звідки,

.

Отже, ми одержали таку нерівність:

.

Якщо – точка неперервності , то при переході до границі в останній нерівності, коли , одержимо: . Тобто існує , а це і означає, що збігається до в основному.