5.1.5. Властивості збіжності у середньому.

Теорема 7. Із збіжності у середньому порядку випливає збіжність за ймовірністю ( ).

Доведення. Використаємо нерівність Чебишова

,

де – довільне, але фіксоване. Якщо , то чисельник правої частини нерівності прямує до 0, тому і права частина теж прямує до 0, а звідси, в свою чергу, випливає, що і ліва частина прямує до 0, а це рівносильне умові .

Теорема 8. Якщо існують , і в середньоквадратичному, то в середньому, і .

Доведення. Із нерівності Ляпунова для моментів

випливає, що із збіжності в середньоквадратичному випливає збіжність в середньому. Оскільки , то із збіжності в середньому випливає, що . За нерівністю

із умов теореми випливає, що із збіжності в середньоквадратичному випливає третє твердження теореми.

Із наведених результатів випливає, що зв’язок між різними видами збіжності можна подати такою схемою:

.

Наведемо деякі приклади, які показують, що в загальному випадку зворотне місця не має.

1. Нехай простір елементарних подій . - борелева -алгебра підмножин відрізка і нехай , – індикатори подій , тоді . Розглянемо послідовність випадкових величин заданих на проміжку і випадкову величину , якщо . Тоді . Тому побудована послідовність збігається за ймовірністю. Але , тому з ймовірністю 1. Тобто, із збіжності не випливає збіжність .

Дослідимо збіжність побудованої послідовності в середньому: 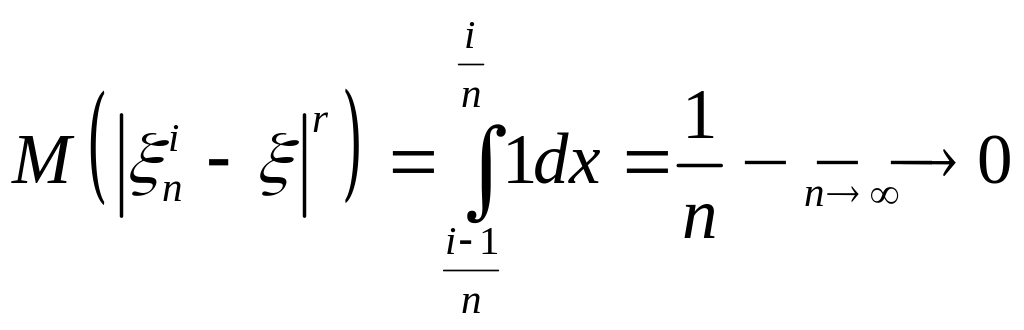. Одержимо, що .

2. Розглянемо послідовність 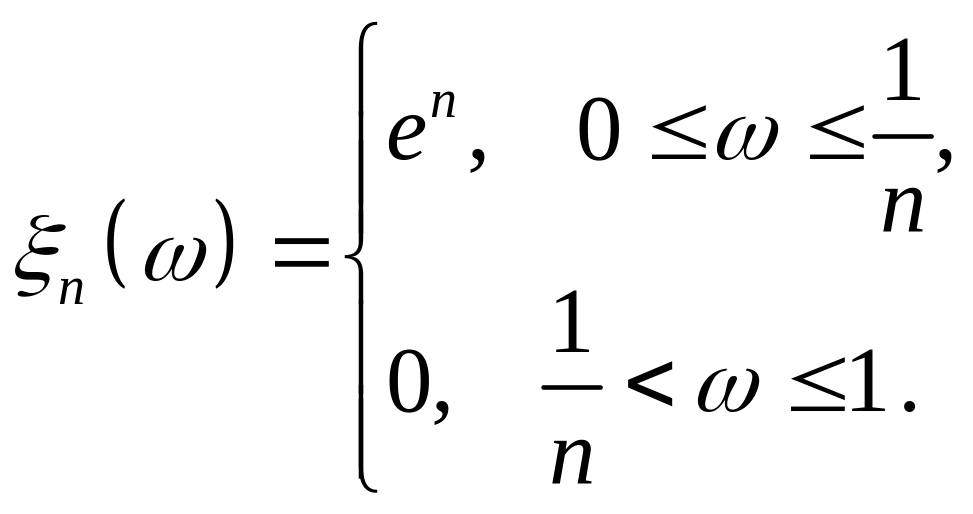. Тоді , і . Отже, , але , тобто, .

Вправа.

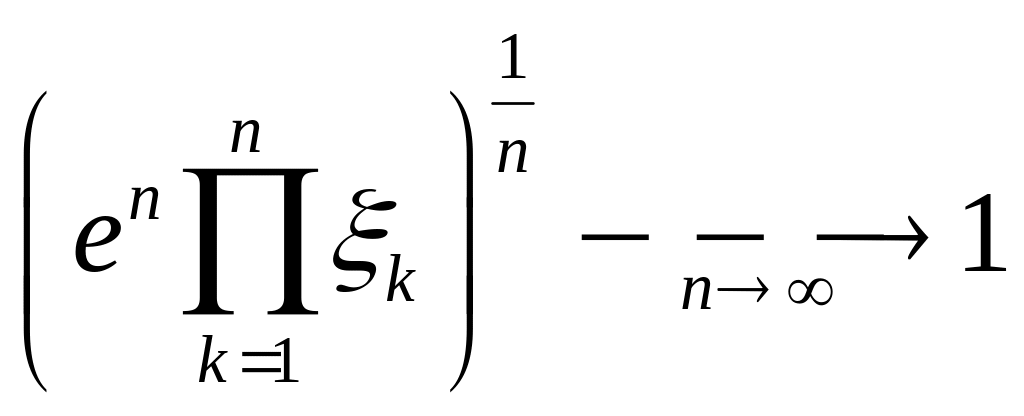1. Нехай – послідовність незалежних випадкових величин, що мають рівномірний на розподіл. Довести, що за ймовірністю.

5.2. Закон великих чисел. Посилений закон великих чисел

5.2.1. Закон великих чисел. Нехай маємо послідовність випадкових величин , розглянемо нову послідовність випадкових величин . Кажуть, що для послідовності має місце закон великих чисел, якщо існує числова послідовність така, що .

Якщо ця збіжність має місце з ймовірністю 1, то кажуть, що має місце посилений закон великих чисел.

Теорема 1 (Чебишова). Якщо випадкові величини – незалежні, мають скінченні математичні сподівання і дисперсії , що рівномірно обмежені сталою , то .

Доведення. Використаємо нерівність Чебишова у вигляді і застосуємо її до випадкової величини . Врахуємо, що

,

.

Тоді . А це означає, що при . Теорема доведена.

Теорема 2 (Бернуллі). Нехай - число появ події в випробуваннях Бернуллі, – ймовірність настання події в кожному випробуванні. Тоді (відносна частота події збігається за ймовірністю до ймовірності появи події).

Доведення. Нехай – число появ події в - му випробуванні, тоді , , , . Отже, виконуються умови теореми 1, тому .

Аналізуючи доведення теореми 1, бачимо, що можна не вимагати незалежності подій і послабити її умови щодо дисперсій.

Теорема 3 (Маркова). Нехай випадкові величини мають скінченні математичні сподівання . Тоді, якщо , то має місце закон великих чисел: при .