4.2. Дисперсія випадкової величини

Математичне сподівання квадрата відхилення випадкової величини від її математичного сподівання називається дисперсією (позначається ):

. (4)

Квадратний корінь із дисперсії називається середнім квадратичним відхиленням або стандартним відхиленням: .

Дисперсія характеризує розсіювання значень випадкової величини відносно її математичного сподівання.

Розглянемо деякі властивості дисперсії.

1. Дисперсія, що характеризує розсіювання відносно математичного сподівання, є найменшою характеристикою розсіювання відносно будь-якого центру , тобто:

.

Дійсно, за властивостями математичного сподівання

,

бо і .

Для будь-якого права частина одержаної рівності . Мінімум досягається, якщо .

В результаті доведення властивості 1 одержуємо таку формулу:

,

що справедлива для будь-якого . Зокрема, покладаючи в останній формулі , одержимо:

. (5)

2. . . Якщо , то з ймовірністю 1 - стала.

Перше очевидне, оскільки . Нехай , тоді , а , тому . Якщо , то із нерівності за властивістю 6 математичного сподівання , тому і або .

Із цієї властивості і (5) одержуємо такі нерівності:

,

.

3. Для будь-яких a і b .

За означенням дисперсії

.

4. .

За властивостями математичного сподівання

.

Величина

називається коваріацією випадкових величин і . Тому

.

Для незалежних випадкових величин і

.

Тому, якщо випадкові величини і – незалежні, то

.

Якщо випадкові величини – незалежні і однаково розподілені, , то

.

Із властивості 11 математичного сподівання випливає нерівність

.

Із властивостей математичного сподівання випливає, що дисперсію можна обчислити за формулами

.

Якщо – дискретна і приймає значення із ймовірностями , то

,

якщо величина має щільність , то

.

Розглянемо приклади обчислення дисперсії.

1. Біномний розподіл. Нехай дорівнює числу появ події в незалежних експериментах. . Нехай – число появ події в і-ому експерименті, тоді приймає два можливих значення: 0 з ймовірністю і 1 з ймовірністю ;

Тоді , . За формулою (5) . Число появ події в експериментах і випадкові величини – незалежні. Тому

2. Розподіл Пуассона. Випадкова величина приймає значення з ймовірностями . Тоді . А

.

Тому

.

3. Рівномірний розподіл на відрізку . Щільність розподілу випадкової величини має вигляд:

Ми уже знайшли . Знайдемо

.

Тоді

.

4. Нормальний розподіл. Нехай випадкова величина має нормальний розподіл з параметрами і . Її щільність і ми уже знайшли . За формулою для обчислення дисперсії

.

Після виконання підстановки , , , одержуємо:

.

Отже, нормальний закон розподілу повністю визначається параметрами і .

Вправи.

4. Нехай випадкова величина набуває значень з ймовірностями . Знайти і .

5. Знайти дисперсію дискретної випадкової величини за законом розподілу із вправи 2.

6. Дискретна випадкова величина приймає два можливих значення і . . Знайти закон розподілу , якщо ; .

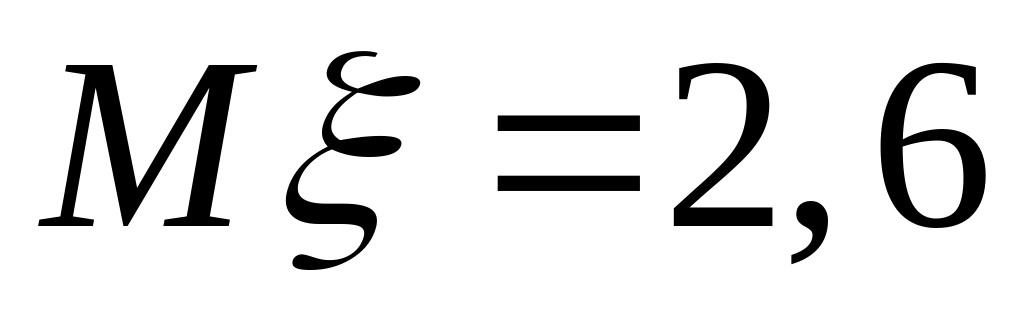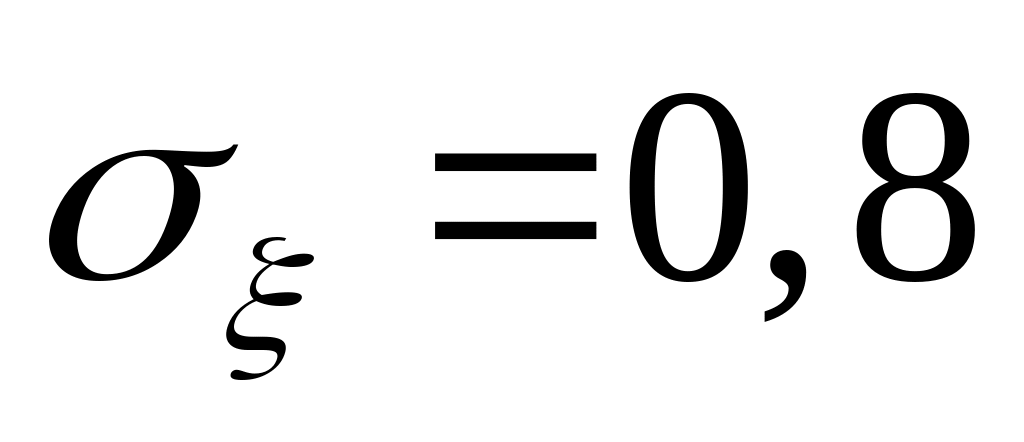7. Тривалість безвідмовної роботи приладу є випадкова величина , що має показниковий розподіл із щільністю 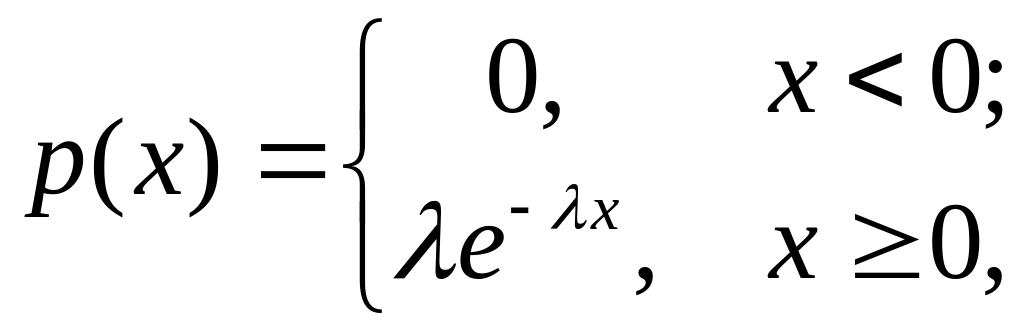. Знайти , , .

8. Задано функцію розподілу випадкової величини Знайти , , .