3.4. Абсолютно неперервні розподіли. Щільність розподілу випадкової величини

Означення. Нехай випадкова величина має функцію розподілу . Якщо існує така інтегровна борелєва функція , що для всіх дійсних x виконується рівність

, (3)

то розподіл називається абсолютно неперервним, а називається щільністю розподілу випадкової величини.

Із означення випливає, що - неперервна. Якщо є точкою неперервності , тоді диференційовна в точці x і . Так як неспадна, то

. (4)

Із (3) і властивості 4 функції розподілу випливає, що

, (5)

врахувавши рівність , одержуємо:

. (6)

Будь-яка функція p(x), для якої мають місце властивості (4) і (5), є щільністю розподілу деякої випадкової величини.

Графік функції називається кривою розподілу. Із (6) випливає, що ймовірність попадання випадкової величини у проміжок дорівнює площі фігури, що обмежена віссю абсцис, графіком кривої розподілу і прямими x= , x= .

Якщо щільність розподілу неперервна, то із рівності (6) при малих

.

Одержана рівність і наближена рівність , що із неї одержується, пояснюють ймовірнісний зміст щільності розподілу.

Відзначимо без доведення таке твердження.

Якщо випадкова величина має щільність розподілу , то для довільної борелєвої множини B має місце рівність

.

Ми розглянули два типи розподілів: дискретний і абсолютно неперервний. Але ними не вичерпуються всі типи розподілів. Сформулюємо теорему А. Лебега.

Теорема. Будь-яка функція розподілу однозначно може бути представлена у вигляді суми

,

де , i=1, 2, 3, , – функція розподілу дискретної випадкової величини, - абсолютно неперервна функція розподілу, - сингулярна функція розподілу, що є неперервною функцією, множина точок росту якої має лебегову міру нуль.

Наведемо приклади найбільш важливих неперервних розподілів.

Рівномірний розподіл на відрізку [a,b]. На відрізок [a,b] випадково кидається точка, причому вважаємо, що всі положення точки рівноможливі. Визначимо випадкову величину , якщо , тобто – координата вибраної точки. В прикладі 1 ми показали, що функція розподілу випадкової величини має вигляд:

Тому щільність розподілу випадкової величини

Значення випадкової величини, що має рівномірний розподіл на відрізку , одержане внаслідок експерименту, називають випадковим числом. На основі випадкових чисел із рівномірного розподілу можна моделювати випадкові величини із будь-яким наперед заданим розподілом.

Нормальний розподіл. Випадкова величина має нормальний розподіл із параметрами і , якщо її щільність розподілу

.

Позначаємо: ~ . Якщо , а , то 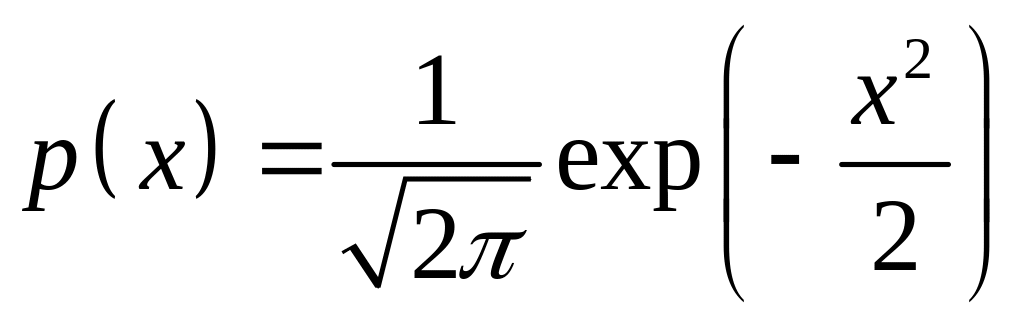– функція Гауса, тоді розподіл називається стандартним.

Функція розподілу має вигляд:

.

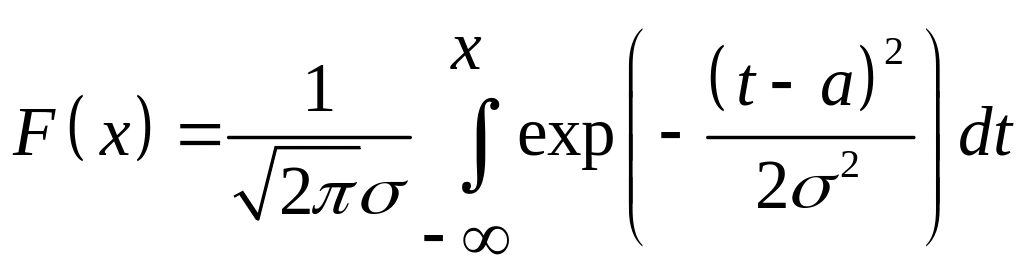Використовуючи інтеграл Пуассона, одержимо:

.

Нехай – функція Лапласа, – функція розподілу стандартного нормального закону, тоді

.

Тобто,

.

Як частинний випадок,

.

Якщо у попередній формулі покласти , то . Тому нормально розподілена випадкова величина з ймовірністю досить близькою до одиниці приймає значення, що відрізняються від параметра a не більше, ніж на .

Якщо випадкова величина ~ , то ~ , тобто буде мати стандартний нормальний розподіл:

.

Показниковий розподіл. Випадкова величина має показниковий розподіл із параметром , якщо

Очевидно,

.

Знайдемо функцію розподілу. Нехай , тоді . Якщо ж , то . Отже,

Відзначимо, що показниковий розподіл має властивість відсутності післядії: при

.

Тобто, при

.

Серед всіх неперервних розподілів цю властивість має тільки показниковий розподіл.

Гамма-розподіл. Розглянемо гамма-функцію . Зробимо в інтегралі заміну , де . Тоді

і

.

Тому для функції

виконуються умови (4) і (5). Отже, вона є щільністю розподілу деякої випадкової величини. Розподіл із такою щільністю називається гамма-розподілом із параметрами .

Вправи.

11. Випадкова величина має показниковий розподіл із параметром . Знайти , .

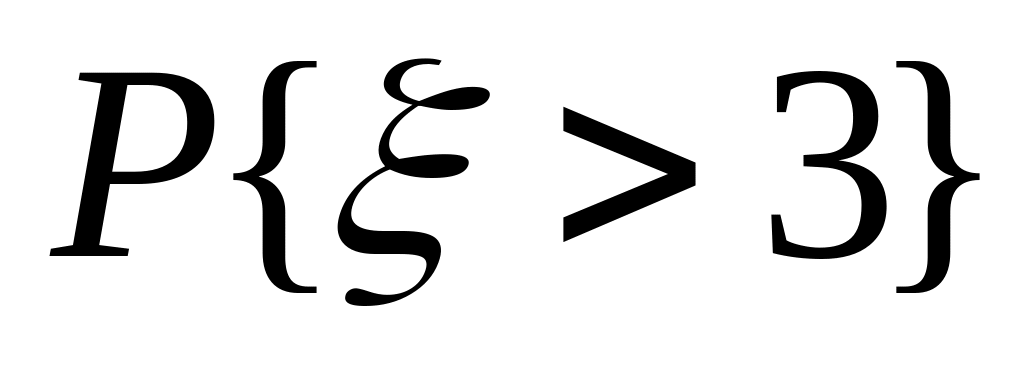12. Функція 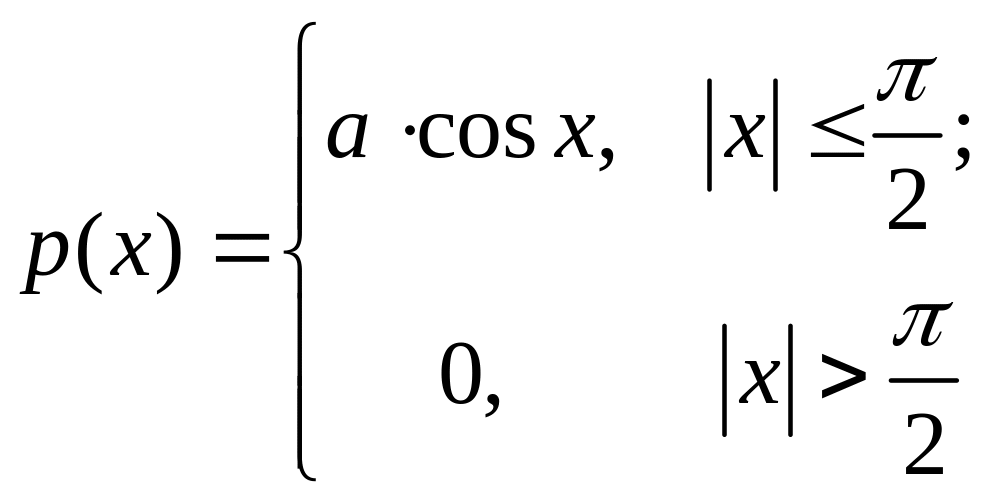є щільністю розподілу випадкової величини . Знайти a і функцію розподілу .

13. Показати, що показниковий розподіл є частинним випадком гамма-розподілу.