Розділ 3. Випадкові величини та їх розподіли

3.1. Випадкові величини. Функція розподілу випадкової величини

Розглядаючи випадкові експерименти, дотепер нас цікавили їх можливі наслідки. Але із можливими наслідками експерименту можна пов’язати певну величину, яка в залежності від наслідку експерименту приймає деякі числові значення. Наприклад, при киданні грального кубика нас цікавить число очок, які є на грані. При контролі якості продукції нас може цікавити число бракованих виробів серед випадково взятих n виробів. При проведенні пострілів по мішені кожній точці попадання ставимо у відповідність величину, яка дорівнює віддалі від цієї точки до центра мішені. Тобто, з кожним експериментом ми пов’язуємо величину, яка в залежності від випадку приймає деякі числові значення. Таку величину називають випадковою. Якщо в експерименті спостерігається певна випадкова величина , то при виборі будь-якого із повинно бути задане значення цієї величини . Отже, випадкову величину можна розглядати, як функцію визначену на просторі елементарних подій . Ця функція повинна задовольняти деяким додатковим умовам. Для цього ми спочатку визначимо поняття борелєвої алгебри.

Розглянемо на множині дійсних чисел R клас всіх напівінтервалів , де . Тоді мінімальна алгебра, яка містить такий клас множин, називається борелєвою. Будемо її позначати . Будь-який елемент борелєвої алгебри називають борелєвою множиною. Зокрема, борелєвими є інтервали, відрізки, одноточкові множини, всі відкриті та замкнені множини. Аналогічно, мінімальна алгебра, яка породжена класом всіх напіввідкритих паралелепіпедів із , називають борелєвою алгеброю підмножин із . Функція називається борелєвою, якщо прообраз будь-якої борелєвої множини в є борелєвою множиною в . Неперервні функції є борелєвими.

Означення 1. Нехай задано ймовірнісний простір . Випадковою величиною називається будь-яка дійсна функція , що відображає простір елементарних подій в множину дійсних чисел R, для якої прообраз будь-якої борелєвої множини є множина із алгебри : .

В теорії функцій такі функції називають вимірними відносно алгебри . Із властивостей вимірних функцій випливає, що в означенні достатньо було вимагати, щоб для довільного дійсного x прообраз півінтервалу належав до .

Сформулюємо деякі висновки, що випливають із властивостей вимірних функцій. Звідси, зокрема, одержуємо, що множини , , , , , є випадковими подіями.

Якщо випадкові величини і визначені на одному і тому ж ймовірнісному просторі, то , , є також випадковими подіями.

Ми будемо також розглядати і події, що пов’язані із нескінченними послідовностями випадкових величин. Нехай - послідовність випадкових величин, що задані на ймовірнісному просторі , і - випадкова величина на . Тоді існує} , .

Із наведених фактів випливають наступні твердження.

Нехай борелєва функція, а ,…, - випадкові величини на , тоді ( ,…, ) є випадковою величиною.

Нехай – послідовність випадкових величин, що задані на ймовірнісному просторі , тоді , , , , є випадковими величинами (можливо невласними – це такі функції , які можуть приймати значення ).

В позначеннях випадкової величини залежність від елементарної події часто не буде вказуватись: замість будемо писати .

Нехай задана випадкова величина . Визначимо на сігма-алгебрі ймовірність за допомогою рівності . Можна показати, що вона задовольняє всім аксіомам ймовірності. Тому можемо розглядати новий ймовірнісний простір , що породжений випадковою величиною .

Означення 2. Ймовірність називається розподілом випадкової величини .

Означення 3. Нехай . Тоді функція називається функцією розподілу випадкової величини . Тобто, функція, яка для кожного дійсного x визначається рівністю

,

називається функцією розподілу випадкової величини .

Функція розподілу випадкової величини повністю визначає її розподіл.

Там, де це не викличе непорозуміння, замість писатимемо . Отже,

.

Як приклад, розглянемо рівномірний розподіл на відрізку [a,b]. На рідрізок [a,b] випадково кидається точка, причому вважаємо, що всі положення точки рівноможливі (ймовірність попадання точки на деяку частину відрізка пропорційна мірі цієї частини). Простір елементарних подій , є -алгебра борелєвих підмножин даного відрізка, P(.) – така міра, що , якщо . Визначимо випадкову величину , якщо , тобто - координата вибраної точки. Тоді для довільного x

Тому і – випадкова величина, а її функція розподілу має вигляд:

Відзначимо, що для різних випадкових величин їх функції розподілу можуть співпадати. Наприклад, нехай , , , , – випадкова величина, що визначена на : Тоді

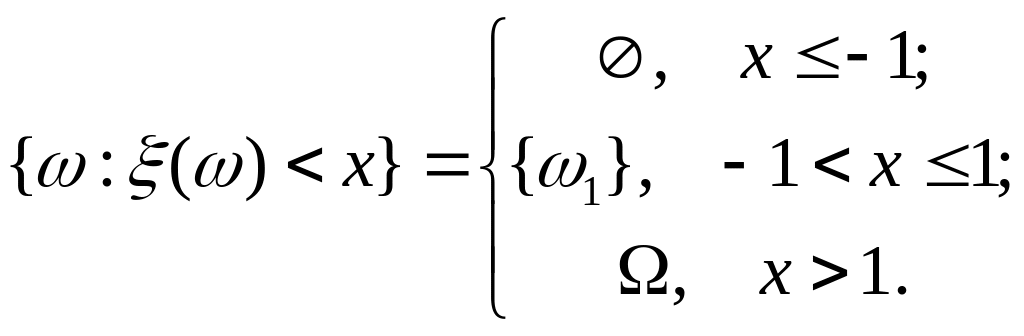
Із визначення функції розподілу одержуємо:

Розглянемо нову випадкову величину Тоді, очевидно,

Якщо , то . Отже, різні випадкові величини можуть мати однакові функції розподілу.

Вправи.

1. В круг із центром в початку координат і радіусом R випадково кидають точку. Нехай - віддаль від даної точки до початку координат. Знайти функцію розподілу випадкової величини .

2. Нехай - довільний ймовірнісний простір, A - деяка випадкова подія. Розглянемо випадкову величину яку називають індикатором випадкової події A. Знайти функцію розподілу даної випадкової величини.