Розділ 2. Схема Бернуллі. Формула Бернуллі

2.1. Послідовність незалежних випробувань. Формула Бернуллі

Нехай послідовно проводяться випадкові експерименти (випробування). Будемо вважати, що будь–яка подія, яка відноситься до фіксованого випробування, буде незалежною від будь–якої події, що відноситься до інших випробувань. Тоді говорять, що задано послідовність незалежних випробувань. Нехай проводиться послідовність незалежних випадкових експериментів, в кожному із яких може настати деяка подія . Якщо ймовірність настання події є однаковою в кожному експерименті, то таку послідовність випробувань називають схемою Бернуллі.

Нехай проводяться серії із n випробувань. Позначимо – ймовірність того, що в випробуваннях подія настане точно разів. Результати серії із n випробувань можна подати у вигляді , де – подія, яка настає в -му експерименті, або . Тоді , якщо в -му експерименті настала подія , і , якщо . Тому, враховуючи незалежність, , а для тих , у яких входить рівно k разів, а n–k разів . Але k випробувань, у яких настає подія , можна вибрати способами і для кожного з них ймовірність рівна . Тоді за аксіомою адитивності,

. (1)

Одержана формула називається формулою Бернуллі.

Оскільки, , то .

Нехай – деяке фіксоване число, – змінне, . Дослідимо поведінку при зміні . Розглянемо відношення

.

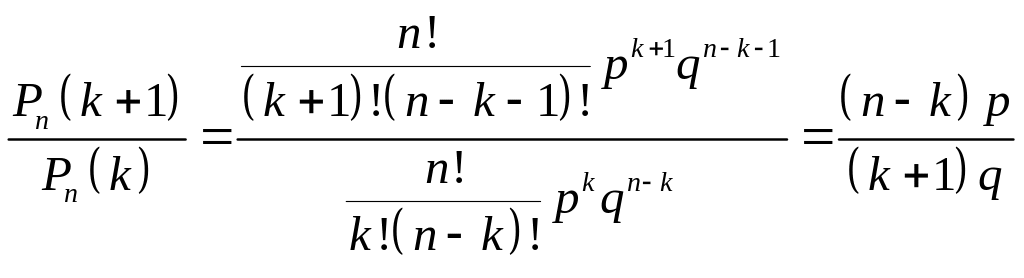Якщо або , то , тобто, ймовірності – зростають. Аналогічно,

при . Тому при ймовірності – спадають. Якщо є цілим числом, то максимальне значення ймовірності досягається при двох значеннях k, а саме: і . Якщо ж не є цілим числом, то максимальне значення ймовірності досягається тільки при одному значенні . Число , при якому є максимальною, називається найімовірнішим числом настання події. При цьому справедлива нерівність

. (2)

Приклад 1. Ймовірність виготовлення на автоматичному верстаті стандартної деталі дорівнює 0,9. Знайти ймовірність того, що із 6 випадково взятих деталей 4 будуть стандартні. Знайти найімовірніше число стандартних деталей із 6 випадково взятих деталей.

Розв’язування. Використаємо формулу Бернуллі: . В нашому випадку , , , тому

. Для знаходження найімовірнішого числа стандартних деталей із 6 випадково взятих деталей застосуємо (2): . Тобто, .

Застосування формули Бернуллі при великих n вимагає великої обчислювальної роботи, при цьому виникають похибки заокруглення, тому результат одержуємо наближений. Ми розглянемо тепер деякі наближені формули, що значно спрощують обчислення ймовірностей в схемі Бернуллі.

Вправи.

1. Ймовірність настання події A в кожному із 8 незалежних випробувань дорівнює 0,6. Знайти: a) найімовірніше число настання події – та ; b) ймовірність того, що подія настане принаймні один раз.

2. Що ймовірніше: виграти у рівносильного супротивника 3 партії із 5, чи 4 партії із 8?

3. Подія B настає, коли подія A настане не менше двох раз. Знайти ймовірність настання події B, якщо буде проведено 6 незалежних випробувань, в кожному із яких .