1.2.5. Наслідки із аксіом.

Н1. Ймовірність неможливої події дорівнює нулю.

Дійсно, , а за третьою аксіомою . Отже, .

Н2. .

Оскільки і , то за аксіомами P2 і P3

.

Для ймовірностей двох протилежних подій використовують позначення: , .

Н3. Якщо – попарно несумісні , то

.

Це випливає із аксіоми P3.

Н4. Якщо – утворюють повну групу , то

.

Випливає із попереднього наслідку і аксіоми P2.

Н5. Якщо , то і .

Подію B можна представити у вигляді , де події і несумісні. Тому за аксіомою P3 або . За аксіомою P1 , тому .

Н6. Для довільної події .

Випливає із того, що і попереднього наслідку.

Н7. Нехай A і B – довільні події. Тоді

.

Цю рівність називають теоремою додавання ймовірностей.

Подію можна представити у вигляді двох несумісних подій і : . Крім того, . Тому за п’ятим наслідком і аксіомою P3 .

Н8. , , .

Перша нерівність випливає із сьомого наслідку, а друга – із першої за методом математичної індукції. Для доведення третьої нерівності введемо такі події: , , , …, , … . Тоді . Визначені події попарно несумісні і , тоді за аксіомою P4 і наслідком 5 .

Вправи.

16. Нехай ; . Довести, що .

17. Довести рівності: , .

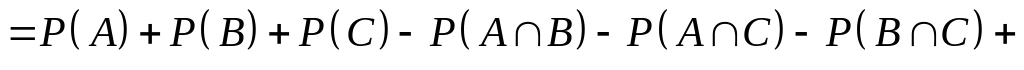
1.2.6. Аксіома неперервності. Наступна теорема показує, що можна сформулювати еквівалентну систему аксіом, змінюючи четверту аксіому.

Нехай – зростаюча послідовність подій, тобто така, що , тоді покладемо . Якщо ж – спадна послідовність подій, тобто така, що , тоді покладемо .

Теорема 1.2. Якщо має місце аксіома скінченої адитивності, то наступні твердження еквівалентні:

1) якщо , такі, що при і , то ;

2) якщо – зростаюча послідовність подій ( ), , , , то ;

3) якщо – спадна послідовність подій ( ), , , , то ;

4) якщо – спадна послідовність подій ( ), , і , то .

Доведення. Проведемо доведення за такою схемою: 1) 2) 3) 4) 1), із якої буде випливати еквівалентність умов 1) – 4).

1) 2). Нехай – зростаюча послідовність подій ( ) із . Покладемо , . Тоді і події будуть попарно несумісними . Тоді , і за третім наслідком . Події попарно несумісні, тому із виконання умови 1) випливає, що

.

2) 3). Нехай – спадна послідовність подій ( ) із , тоді – зростаюча. Застосовуючи умову 2) до , одержимо

.

3) 4). Оскільки виконуються умови 3) і , то .

4) 1). Нехай , такі, що при і . Тоді , де . Послідовність – спадна і , тому за умовою 4) . За властивістю скінченної адитивності

.

Переходячи до границі в останній рівності при і, враховуючи, що ліва частина не залежить від , а , одержимо

.

Теорема доведена.

Кожне із тверджень 2), 3), 4) називають аксіомою неперервності ймовірності. Твердження 2) і 3) можна сформулювати в такому вигляді: якщо – монотонна послідовність подій, то . Властивість, що виражається такою рівністю, називають властивістю неперервності ймовірнісної міри.

1.3. Умовні ймовірності. Незалежність подій

1.3.1. Умовні ймовірності. Теорема множення. Розглядаючи ймовірності випадкових подій, ми не мали ніякої інформації про ймовірнісний зв’язок між різними випадковими подіями. Очевидно, він існує. Якщо при обчисленні ймовірності події A не накладається додаткових умов, крім тих, якими визначається випадковий експеримент, то ймовірність називають безумовною. Але в ряді випадків необхідно обчислити ймовірності подій при додатковій умові, що настала деяка подій B, яка має додатню ймовірність. Ймовірність події A, обчислена за припущенням, що подія B уже настала, називається умовною ймовірністю події A при умові B і позначається або .

Розглянемо приклад знаходження умовної ймовірності в класичній моделі. Позначимо , , кількість елементарних подій, що спричиняють відповідно події , , . Тоді

.

Якщо подія B уже настала, то змінюються умови експерименту і у новому (умовному) експерименті число можливих наслідків буде рівне – числу елементарних подій, що спричиняють подію , а подію A будуть спричиняти тільки ті елементарні події, які спричиняють . Тому

.

У загальному випадку умовна ймовірність вводиться за допомогою наступного означення.

Означення. Умовною ймовірністю події при умові, що подія настала з , називається число

.

Аналогічно, при виконанні умови ,

.

Введена таким чином умовна ймовірність має всі властивості ймовірності. Для перевірки цього досить показати, що виконуються аксіоми ймовірності. Із означення і властивостей ймовірності випливає:

1) ,

2) ,

3) ,

4) якщо , то ,

5) якщо – послідовність попарно несумісних подій ( при ), то .

6) .

Властивості 2) і 3) випливають із 4), тому доведемо 4) і 5).

Якщо , то , тому .

.

Нехай – сігма-алгебра подій , де , а – фіксована, тоді , , – буде ймовірнісним простором.

Із означення умовної ймовірності одержуємо твердження, яке називається теоремою множення ймовірностей.

Теорема 1. Якщо і , то

.

Теорема 2. Якщо – такі випадкові події, що , тоді

( загальна теорема множення ймовірностей).

Доведення. Оскільки для довільного , то

, а це означає, що всі умовні ймовірності в теоремі визначені. Застосовуючи теорему 1, одержимо

.

Теорема доведена.

Приклад 1. В урні є 10 куль: 3 білих і 7 чорних. Із урни випадково вибирають дві кулі. Знайти ймовірність того, що вибрані кулі будуть білі.

Розв’язування. Експеримент, що розглядається в даній задачі, полягає у виборі двох куль із десяти. Нехай A – подія, яка полягає у тому, що перша вибрана куля буде білою, а B – друга вибрана куля буде білою. Тоді – обидві вибрані кулі будуть білі. За класичним означенням . Якщо A настала, то в урні залишилось дев’ять куль, із яких дві білі, тому . Отже, за теоремою множення .

Вправи.

18. Монету підкидають три рази. Описати простір елементарних подій; описати події: A – двічі випав герб, B – принаймні один раз випав герб; обчислити , і .

19. Підкидаються два гральні кубики. Знайти ймовірність того, що випаде принаймні одна шістка, якщо випала сума очок рівна 8.

20. Дано: , , . Знайти .

21. Студент підготував 20 із 25 питань програми. Знайти ймовірність того, що студент знає відповіді на випадково запропоновані йому три питання.

22. Події A і B – несумісні і . Обчислити .

1.3.2. Незалежність подій. Розглянемо тепер одне із найважливіших понять теорії ймовірностей – поняття незалежності випадкових подій. Саме це поняття виділило теорію ймовірностей із теорії міри і теорії функцій в самостійну дисципліну.

Означення 1. Події і називаються незалежними, якщо

.

Теорема 1.3. Для того, щоб події і були незалежними, необхідно і досить, щоб виконувалась одна із умов: (якщо ); або (якщо ).

Доведення. Якщо події і незалежні, то , а за теоремою множення , тому і . Тобто і . І навпаки, нехай, наприклад, . Тоді за теоремою множення . Отже, події незалежні. Теорема доведена.

Таким чином, незалежність подій означає, що настання однієї із подій не змінює ймовірності іншої. На практиці висновок про незалежність подій роблять на основі незалежності експериментів, із якими ці події пов’язані.

Приклад 2. Двічі підкидають монету. Нехай подія A – при першому підкиданні випадає герб, B – при другому підкиданні випадає герб. Обчислити , , , . Показати, що події A і B незалежні.

Розв’язування. Простір елементарних подій складається із чотирьох рівноможливих елементарних подій: – ГГ, – ЦЦ, – ГЦ, – ЦГ. Тоді , , , а , , . Події A і B незалежні, бо .

Умовну ймовірність знайдемо за означенням: .

Висновок про незалежність подій і можемо зробити і на основі попередньої теореми: , тому події і незалежні.

Приклад 3. В кожному із двох ящиків міститься по 10 куль: в першому – 8 білих і 2 чорні, в другому – 7 білих і 3 чорні. З кожного ящика вибирають по одній кулі. Знайти ймовірність того, що ці кулі будуть білі.

Розв’язування. Нехай подія A – куля, що вибрана із першого ящика, є білою, B – куля, що вибрана із другого ящика, є білою, тоді – обидві кулі є білими. Так як , , а події A і B – незалежні, то .

Теорема 1.4. Якщо події і незалежні, то незалежними будуть і події і , і , і .

Доведення. Так як і , то із незалежності подій

( ) одержуємо

.

Отже і незалежні. Аналогічно,

,

що означає незалежність подій і . І, нарешті,

.

Тобто, і незалежні. Теорема доведена.

Приклад 4. Для сигналізації про аварію встановлено два незалежно працюючих сигналізатори. Ймовірність того, що при аварії перший сигналізатор спрацює, дорівнює 0,7, а другий – 0,8. Знайти ймовірності таких подій: A – при аварії спрацює тільки один сигналізатор; B – при аварії сигнал про аварію буде поданий.

Розв’язування. Нехай – подія, яка полягає в тому, що при аварії i – й ( ) сигналізатор спрацює. Подія A настає, якщо спрацьовує тільки перший (подія ) , або тільки другий сигналізатор (подія ), тому . За умовою , , події і несумісні, а події і незалежні (сигналізатори працюють незалежно), тоді

.

Для знаходження ймовірності події B вигідніше перейти до протилежної події. Подія настає, якщо не спрацює жодний сигналізатор, тобто, . Тоді , а .

Даний приклад показує, що уже елементарні поняття теорії ймовірностей мають практичне застосування – пояснюється підвищення надійності при дублюванні.

Означення 2. Події називаються попарно незалежними, якщо кожні дві – незалежні.

Означення 3. Події називаються незалежними або незалежними в сукупності, якщо для будь-якого і для будь-яких

.

Із незалежності в сукупності подій випливає їх попарна незалежність, але не навпаки. Нехай, наприклад, і всі елементарні події рівноможливі. Тоді події , , попарно незалежні, але не є незалежними в сукупності. Дійсно, , тому

,

, , ,

але .

Відзначимо також, що із того, що для деяких подій A, B, C

,

ще не випливає попарна незалежність цих подій. Дійсно, нехай і всі пари рівноможливі. Тоді для , , маємо , , , , , але .

Вправи.

23. Події – незалежні. Довести, що .

24. Ймовірність того, що при аварії сигналізатор спрацює, дорівнює 0,7. Скільки необхідно встановити незалежно працюючих сигналізаторів, щоб із ймовірністю, яка не менше 0,9, при аварії сигнал про аварію був поданий.

25. Перший стрілець влучає в ціль з ймовірністю 0,6, другий – 0,5, а третій – 0,4. Стрільці зробили залп по цілі. Відомо, що є два влучення. Що більш ймовірно: попав третій стрілець у ціль, чи ні?

26. Розрив електричного кола настає внаслідок виходу із ладу елемента К або двох елементів К₁ і К₂, які виходять з ладу незалежно один від одного відповідно з ймовірностями 0,3; 0,2 і 0,2. Знайти ймовірність розриву електричного кола.

27. Довести, що коли події і незалежні і , то або .

28. Довести, що якщо і , то події і – незалежні.

1.3.3. Формула повної ймовірності. Формули Байєса. Нехай подія може настати із однією із подій , що утворюють повну групу і , . Це означає, що події попарно несумісні і . Тоді . Із попарної несумісності подій випливає, що події також попарно несумісні, тому . Тобто,

.