
- •Содержание
- •Предисловие
- •Глава I. Нелинейное программирование: экстремумы функций нескольких переменных
- •§1. Классические методы оптимизации
- •1.1. Безусловный экстремум функции одной переменной
- •1.2. Условный экстремум функции одной переменной
- •1.3. Безусловный экстремум функций двух переменных
- •1.4. Упражнения.
- •§2. Безусловный экстремум функций нескольких переменных
- •2.1. Необходимые и достаточные условия
- •§3. Условный экстремум функций нескольких переменных
- •3.1. Основные определения и факты
- •3.2. Условный экстремум при ограничениях типа равенств
- •3.3. Условный экстремум при ограничениях типа неравенств
- •3.4. Условный экстремум при смешанных ограничениях
- •3.5. Понятие о методах штрафных функций
- •Глава II. Численные методы нелинейного программирования
- •§1. Общие положения
- •1.1. Постановка проблемы
- •1.2. Общие принципы.
- •§2. Методы нулевого порядка одномерной минимизации
- •2.1. Общие положения
- •2.2. Метод равномерного поиска
- •2.3. Метод деления интервала пополам
- •§3. Методы первого и второго порядка
- •3.1. Метод градиентного спуска с постоянным шагом
- •3.2. Метод Ньютона
- •§4. Элементы численных методов задачи условной оптимизации выпуклого программирования
- •4.2. Постановка задачи выпуклого программирования.
- •4.3. Численные методы на основе метода штрафных функций
- •4.4. Метод проекции градиента.
- •Приложение 1. Варианты индивидуальных заданий
- •Задание нп-1
- •Задание нп-2
- •Задание нп-3
- •Задание нп-4
- •Задание нп-5
- •Задание нп-6
- •Задание нп-7
- •Задание нп-8
1.2. Условный экстремум функции одной переменной
В стандартных курсах высшей математики (или математического анализа) рассматривается задача нахождения экстремумов функции одной переменной y=f(x) на некотором отрезке [a, b]. Эта задача формулируется в виде (1). Действительно, отрезок [a, b] может быть решением некоторого неравенства, например, неравенства x2(a+b)+ab0. Поэтому эту задачу можно сформулировать в виде (1) так:
f(x) max(min)
x2(a+b)+ab0.
Эта задача решается по следующей схеме:
1. Найти производную функции y=f(x).
2. Решив уравнение y=0, найти стационарные точки функции.
3. Вычислить значения функции в стационарных точках и на концах отрезка [a, b].
4. Выделить из значений функции, вычисленных в пункте 3, наибольшее и наименьшее значения.
Пример III. Найти наибольшее и наименьшее значения функции y=4x3+9x2+6x1 на отрезке [2, 3].
Решение. 1. Найдём у функции производную: y=12x2+18x+6.
2. Решая уравнение y=0, найдём стационарные точки функции:
y=0 x1= , x2=1 стационарные точки функции
(подробности см. решение Примера I)
3. Вычислим значения функции в стационарных точках и на концах отрезка [2, 3]:
f(1)=2, f = (подробности см. решение Примера I),
f(2)=4(2)3+9(2)2+6(2)1=3, f(3)=433+932+631=206.
4. Сравнивая полученные в предыдущем пункте значения функции, выделяем из них наибольшее и наименьшее значения: fнаим(x)=f(2)=3, fнаиб(x)=f(3)=206.
Ответ: fнаим(x)=3 достигается в точке x=2,
fнаиб(x)=206 достигается в точке x=3.
1.3. Безусловный экстремум функций двух переменных
Напомним, что в данном параграфе мы рассматриваем классические методы оптимизации, и для функций нескольких переменных ограничиваемся двумя переменными: z=f(x, y). Также напомним, что в отношение вектора возможно одновременное применение в качестве обозначений как строки, так и столбца. При чтении произведений типа AX или XA, где X вектор, а A (mn)-матрица, разночтений быть не должно: в первом случае это столбец с n элементами, во втором строка с m элементами.
1.3.1. (Необходимое условие экстремума функции двух переменных) Пусть X*=(x0, y0)R2 точка локального минимума (максимума) функции z=f(x, y) на множестве R2 и z=f(x, y) дифференцируема в точке X*. Тогда градиент функции z=f(x, y) в точке X* равен нулю:
z(X*)=0, (1.3.1)
что равносильно системе
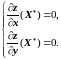 (1.3.2)
(1.3.2)
Точки, удовлетворяющие условиям (1.3.1) или (1.3.2), называются стационарными.
Условия 1.3.1 и 1.3.2 являются необходимыми условиями экстремума, но не достаточными. Действительно, для функции f(x, y)=x3y3 точка X*=(0, 0) является стационарной точкой, так как
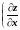 ,
,
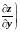 =0
(3x2,
3y2)=0
(х,
y)=0
=0
(3x2,
3y2)=0
(х,
y)=0
(то есть выполняются условия (1.3.1) и (1.3.2)). Но эта точка не является точкой экстремума, так как существуют точки X1 и X2, в которых имеют место неравенства f(X1)<f(X*)<f(X2): достаточно взять X1=(0; ) и X2=(; 0), где >0 сколь угодно малое число.
Для того, чтобы проверить, является ли стационарная точка точкой экстремума, используются следующие достаточные условия экстремума:
1.3.2.
(Достаточные условия экстремума функции
двух переменных)
Пусть функция
z=f(x,
y)
в точке X*=(x0,
y0)
дважды дифференцируема,
z(X*)=0
и
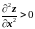 или
или
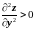 ,
,
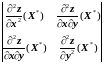 >0
(
>0
(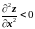 или
или
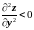 ).
Тогда точка
X*
является точкой локального минимума
(максимума)
функции
z=f(x,
y)
на R2.
).
Тогда точка
X*
является точкой локального минимума
(максимума)
функции
z=f(x,
y)
на R2.
Другими
словами, в точке X*=(x0,
y0)
функция z=f(x,
y)
достигает своего экстремума, если
(X*)=
>0;
при этом вид экстремума будет минимумом,
если
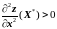 или
или
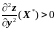 ,
и максимумом при
,
и максимумом при
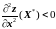 или
или
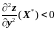 .
.
Отметим, что если (X*)<0, то в точке X* экстремума нет, а при (X*)=0 экстремум может существовать, а может и не существовать. В этом случае для решения вопроса требуются дополнительные исследования.
Таким образом, для того, чтобы исследовать функцию двух переменных на безусловный экстремум (то есть найти для функции точки экстремумов, определить их характер и вычислить значения функции в этих точках), достаточно:
Найти у функции частные производные первого порядка.
Решив систему (1.3.2), найти стационарные точки функции.
Найти у функции частные производные второго порядка и составить матрицу H(X)=
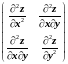 .
.Определить, какие из стационарных точек являются точками максимума, какие точками минимума, какие ни тем, ни другим. Для этого вычислить определитель (X*)= , и если (X*)<0, то X* не является точкой экстремума. Если (X*)>0, то X* точка экстремума, и по знаку
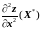 или
или
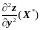 определить вид экстремума.
определить вид экстремума.
Вычислить значения функции в точках экстремума.
Пример IV. Исследовать функцию z=2x2+3xy+2y2+3x3y+2 на безусловный экстремум.
Решение.
1. Найдём у функции частные производные
первого порядка:
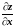 =4x+3y+3,
=4x+3y+3,
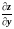 =3x+6y3.
=3x+6y3.
2. Решая систему (1.3.2), найдём стационарные точки функции:
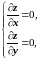
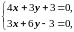
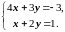
Применив
к последней системе, например, правило
Крамера, получаем (x,
y)=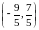 ,
то есть X*=
стационарная точка.
,
то есть X*=
стационарная точка.
3.
Найдём у функции частные производные
второго порядка и составим матрицу
H(X)=
:
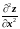 =4,
=4,
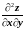 =
=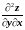 =3,
=3,
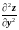 =6,
H(X)=
=6,
H(X)=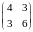 .
.
4.
Так как = =27>0,
то в точке X*=
функция достигает своего экстремума.
При этом
=4>0.
Поэтому в точке X*
функция достигает минимума.
=27>0,
то в точке X*=
функция достигает своего экстремума.
При этом
=4>0.
Поэтому в точке X*
функция достигает минимума.
5. Вычисляем значение функции в точке минимума:
fmin(x,
y)=f
=2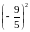 +3
+3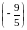
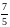 +2
+2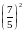 +3
3
+2=
+3
3
+2=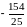 .
.
Ответ: fmin(x, y)= достигается в точке , точек максимума у функции нет.
Пример V. Исследовать функцию z=3xyxy2x2y на безусловный экстремум.
Решение. 1. Найдём у функции частные производные первого порядка: =3yy22xy, =3x2xyx2.
2. Решая систему (1.3.2), найдём стационарные точки функции:
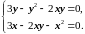
Вычитая из первого уравнения системы второе, приходим к уравнению 3y3xy2+x2=0. Дальнейшие очевидные преобразования приводят к уравнению (yx)(3yx)=0. Дальше рассмотрим отдельно два случая:
Случай 1. yx=0, то есть y=x. Подставляя это равенство, например, в первое уравнение системы, получаем уравнение 3x3x2=0, решениями которого являются x1=0 и x2=1. Тогда решениями системы являются Х1=(0, 0) и Х2=(1, 1).
Случай 2. 3yx=0, то есть y=3x. Подставляя это равенство во второе уравнение системы, получаем уравнение 3x+x2=0, решениями которого являются x1=0 и x2=3. Тогда y1=30=3, y2=33=0, и решениями системы являются Х3=(0, 3) и Х4=(3, 0).
3. Найдём у функции частные производные второго порядка и составим матрицу H(X):
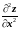 =2y,
=2х,
=
=32(x+y),
H(X)=
=2y,
=2х,
=
=32(x+y),
H(X)=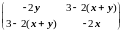 .
.
4. Определим, какие из стационарных точек Х1=(0, 0), Х2=(1, 1), Х3=(0, 3) и Х4=(3, 0) являются точками максимума, какие точками минимума, какие ни тем, ни другим. Для этого для каждой из стационарных точек X* находим значение (X*)=|H(X*)|, и если (X*)>0, то определяем вид экстремума.
Пусть
X*=Х1=(0,
0). Тогда H(X1)=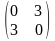 и (X1)=9<0.
Значит, Х1=(0,
0) не является точкой экстремума.
и (X1)=9<0.
Значит, Х1=(0,
0) не является точкой экстремума.
Пусть
X*=Х2=(1,
1). Тогда H(X2)=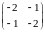 и (X2)=3>0.
Значит, Х2=(0,
0) является точкой экстремума. Так как
(X2)=2<0,
то в этой точке достигается максимум.
и (X2)=3>0.
Значит, Х2=(0,
0) является точкой экстремума. Так как
(X2)=2<0,
то в этой точке достигается максимум.
Для
точек X3
и X4
имеем H(X3)=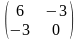 ,
H(X4)=
,
H(X4)=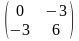 ,
(X3)=(X4)=9<0,
и эти точки не являются точками экстремума.
,
(X3)=(X4)=9<0,
и эти точки не являются точками экстремума.
Таким образом, из стационарных точек только точка X2 является точкой экстремума точкой максимума.
5. Вычисляем значение функции в этой точке:
fmax(x, y)=f(X2)=311112121=1.
Ответ: (1, 1) точка локального максимума, fmax(X)=1.
1.4. Условный экстремум функций двух переменных. В стандартных курсах высшей математики (математического анализа), как правило, ограничиваются задачей условного экстремума функции двух переменных с одним ограничением типа равенства:
f(x, y) min (max)
(x, y)=0 (1.4.1)
Множество, определяемое ограничением (x, y)=0, обозначим через М.
Функция
L(x, y, )=f(x, y)+(x, y) (1.4.2)
называется классической функцией Лагранжа, число множитель Лагранжа.
1.4.1.
(Необходимые условия условного экстремума
функции от двух переменных с одним
ограничением).
Пусть X*=(x0,
y0)R2
точка
локального минимума
(максимума)
функции
z=f(x,
y)
на множестве
М.
Тогда
существует число
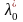 0
такое,
что выполняются
условия:
0
такое,
что выполняются
условия:
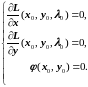 (1.4.3)
(1.4.3)
Точки,
удовлетворяющие системе (1.4.3) при
некотором
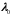 ,
называются условно-стационарными.
,
называются условно-стационарными.
Ясно,
что условия (1.4.3)
не что иное, как необходимое условие
экстремума функции Лагранжа (так как
 ).
Поэтому решение задачи (1.4.1) сводится к
исследованию функции Лагранжа (1.4.2) на
безусловный экстремум. В общем случае
решение этой задачи рассматривается
ниже. Мы же к данному моменту умеем
исследовать на безусловный экстремум
только функцию двух переменных. А пока
предлагаем следующую схему решения
задачи (1.4.1).
).
Поэтому решение задачи (1.4.1) сводится к
исследованию функции Лагранжа (1.4.2) на
безусловный экстремум. В общем случае
решение этой задачи рассматривается
ниже. Мы же к данному моменту умеем
исследовать на безусловный экстремум
только функцию двух переменных. А пока
предлагаем следующую схему решения
задачи (1.4.1).
1) Построить классическую функцию Лагранжа (1.4.2).
2)
Найти частные производные
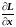 ,
,
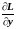 функции Лагранжа.
функции Лагранжа.
3) Решая систему (1.4.3) найти условно-стационарные точки.
4) Вычислить значения функции z=f(x, y) в точках X*=(x0, y0) для условно-стационарных точек (X*, )=(x0, y0, ).
5) Если значения функции z=f(x, y) для различных X* не совпадают, то выбрать из них наибольшее и наименьшее значения. Они и будут искомыми условными экстремумами.
6) Если значения функции z=f(x, y) для всех X* совпадают, в частности, если условно-стационарная точка единственна (решение системы (1.4.3) единственное), то по некоторым другим признакам определяем, какой вид экстремума достигается в точке (x0, y0). Например, взяв точку, координаты (x1, y1) которой удовлетворяют уравнению (x, y), отличную от (x0, y0), вычисляем значение функции в этой точке и сравниваем с f(x0, y0). Если f(x0, y0)<f(x1, y1), то (x0, y0) точка условного минимума, а если f(x0, y0)>f(x1, y1), то (x0, y0) точка условного максимума.
Пример VI. Исследовать на условный экстремум функцию:
f(x, y)=x+yextr
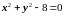 .
.
Решение.
В нашем случае (x,
y)=
(Х)=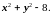
Составим обобщённую функцию Лагранжа:
L(x, y, )=x+y+( ).
Найдём частные производные функции L(x, y, ):
=1+2x, =1+2y.
Решим систему (1.4.3):
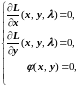
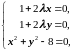
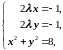
Из
первых двух уравнений системы получаем
x=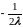 ,
y=
,
подставляя которые в третье, имеем
,
y=
,
подставляя которые в третье, имеем
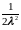 =8
=8
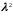 =
=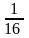
=
=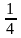 .
Отсюда x=
.
Отсюда x=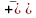 2,
y=
2,
то есть (X1,
1)=(2,
2,
2,
y=
2,
то есть (X1,
1)=(2,
2,
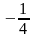 ),
(X2,
2)=(2,
2,
)
две условно-стационарные точки.
),
(X2,
2)=(2,
2,
)
две условно-стационарные точки.
Вычислим значения функции в точках X1=(2, 2) и X2=(2, 2) для условно-стационарных точек (X1, 1)=(2, 2, ) и (X2, 2)=(2, 2, ) (решений системы (1.4.3)):
f(X1)=f(2, 2)=2+2=4, f(X2)=f(2, 2)=22=4.
Так как f(X1)=4>4=f(X2), то есть f(X1)>f(X2), то в точке X1=(2, 2) достигается условный максимум функции z=x+y, а в точке X2=(2, 2) достигается условный минимум.
Ответ: X1=(2, 2) точка регулярного условного локального максимума, f(X1)=4, X2=(2, 2) точка регулярного условного локального минимума, f(X2)=4.
