Задание нп-5
Исследовать на условный экстремум функцию
f(x1,
x2)=(x1a1)2+(x2a2)2
при условиях
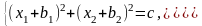
№ в-та |
a1 |
a2 |
b1 |
b2 |
c |
d |
№ в-та |
a1 |
a2 |
b1 |
b2 |
c |
d |
1 |
0 |
6 |
0 |
4 |
25 |
16 |
11 |
0 |
5 |
0 |
5 |
25 |
16 |
2 |
4 |
0 |
5 |
0 |
36 |
9 |
12 |
6 |
0 |
4 |
0 |
25 |
16 |
3 |
0 |
5 |
0 |
5 |
9 |
16 |
13 |
0 |
3 |
0 |
4 |
25 |
9 |
4 |
5 |
0 |
4 |
0 |
36 |
9 |
14 |
5 |
0 |
5 |
0 |
9 |
16 |
5 |
0 |
6 |
0 |
5 |
16 |
16 |
15 |
0 |
6 |
0 |
5 |
25 |
16 |
6 |
6 |
0 |
5 |
0 |
49 |
16 |
16 |
3 |
0 |
4 |
0 |
25 |
9 |
7 |
0 |
4 |
0 |
6 |
16 |
25 |
17 |
0 |
6 |
0 |
4 |
25 |
16 |
8 |
3 |
0 |
5 |
0 |
25 |
16 |
18 |
4 |
0 |
6 |
0 |
16 |
25 |
9 |
0 |
4 |
0 |
5 |
36 |
9 |
19 |
0 |
5 |
0 |
4 |
36 |
9 |
10 |
4 |
0 |
6 |
0 |
25 |
16 |
20 |
6 |
0 |
5 |
0 |
16 |
16 |
Задание нп-6
Решить задачу f(x)=ax2+bx+c min методом:
а) равномерного поиска;
б) деления интервала пополам:
№ в-та |
a |
b |
c |
№ в-та |
a |
b |
c |
№ в-та |
a |
b |
c |
№ в-та |
a |
b |
c |
1 |
3 |
6 |
5 |
6 |
2 |
5 |
2 |
11 |
3 |
8 |
3 |
16 |
2 |
4 |
7 |
2 |
2 |
5 |
3 |
7 |
4 |
2 |
4 |
12 |
4 |
2 |
6 |
17 |
3 |
7 |
7 |
3 |
5 |
3 |
2 |
8 |
2 |
6 |
3 |
13 |
2 |
8 |
4 |
18 |
2 |
2 |
3 |
4 |
4 |
5 |
3 |
9 |
3 |
4 |
2 |
14 |
5 |
3 |
8 |
19 |
3 |
5 |
3 |
5 |
3 |
4 |
6 |
10 |
4 |
2 |
6 |
15 |
4 |
3 |
6 |
20 |
2 |
5 |
2 |