2.7. Электростатика

Электростатика изучает взаимодействие неподвижных заряженных тел.

Электрический заряд q (Кл) — количественная мера электромагнитного взаимодействия между телами.

В дальнейшем под электрическим зарядом (зарядом) будем подразумевать заряженное тело.

Точечный заряд – это заряженная материальная точка.

Заряды бывают двух видов: положительные и отрицательные. Одноименные заряды отталкиваются, а разноименные заряды — притягиваются.

Дискретность заряда: любой заряд состоит из целого числа элементарных зарядов:

q = N e,

где e =  1,610^19 Кл  элементарный заряд.

Элементарный электрический заряд — заряд, которым обладают элементарные частицы — электрон и протон. Положительным элементарным зарядом обладает протон, отрицательным — электрон.

Закон сохранения заряда:

В электроизолированной системе алгебраическая сумма зарядов постоянна.

Q = q₁ + q₂++q_n = const.

Закон Кулона:

Два точечных заряда взаимодействуют с силой, прямо пропорциональной произведению их модулей и обратно пропорциональной квадрату расстояния между ними. Сила Кулона направлена вдоль линии, соединяющей эти заряды.

где k = 1/(4₀) = 9 10⁹ (Нм² / Кл² )  коэффициент пропорциональности;

₀ = 8,8510^12 Ф/м  электрическая постоянная.

Заряженную сферу или заряженный шар можно заменить таким же по значению точечным зарядом, находящимся в центре.

Направление кулоновской силы определяется знаками взаимодействующих зарядов.

Электрическое поле — материальная субстанция, через которую осуществляется взаимодействие электрических зарядов.

Электростатическое поле — поле, создаваемое неподвижными зарядами.

Напряженность (В/м), (Н/Кл) электрического поля — векторная величина, равная отношению силы , с которой электрическое поле действует на положительный точечный заряд q₀ (пробный заряд), помещенный в данную точку поля, к величине этого заряда:

Вектор напряженности электрического поля совпадает по направлению с кулоновской силой, действующей на положительный заряд, помещенный в данную точку электрического поля.

Электрическое поле точечного заряда.

Напряженность Е электрического поля, создаваемого точечным зарядом q в вакууме на расстоянии r от заряда:

,

q > 0 — вектор напряженности направлен от заряда.

q < 0 — вектор напряженности направлен к заряду.

Силовая линия — линия, касательные к которой в каждой точке совпадают с вектором напряженности электрического поля.

Силовые линии начинаются на положительных зарядах и оканчиваются на отрицательных.

Однородным называется электрическое поле, в котором вектор напряженности одинаков во всех точках. Силовые линии однородного поля — параллельные прямые.

Принцип суперпозиции полей (для напряженности): напряженность поля системы зарядов равна векторной сумме напряженностей полей каждого из зарядов.

Потенциал  энергетическая характеристика электрического поля. Потенциал численно равен отношению потенциальной энергии W_p пробного заряда, помещенного в данную точку электрического поля, к величине этого заряда q₀.

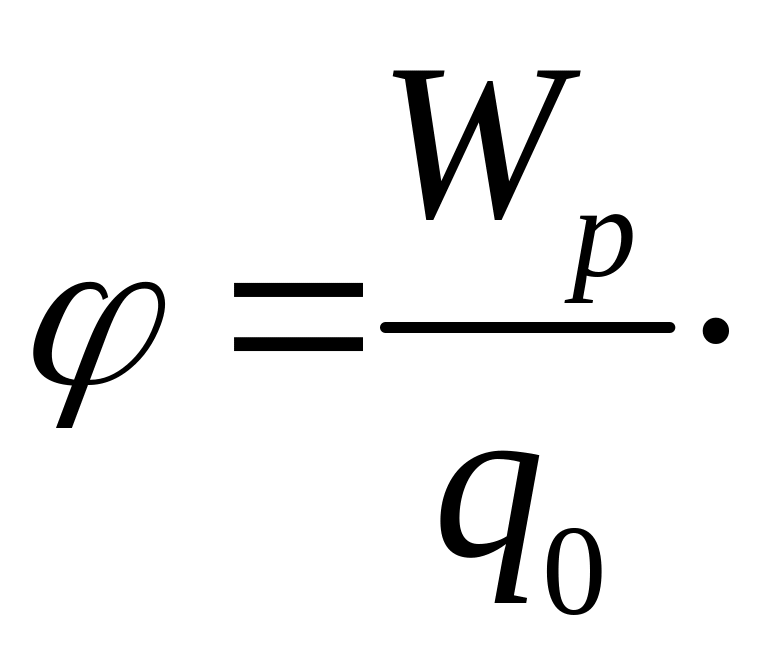
Потенциал численно равен работе, совершаемой полем, при перемещении заряда + 1 Кл из данной точки поля в бесконечность. Потенциал бесконечно удаленной точки поля считается равным нулю.

Потенциал поля точечного заряда определяется по формуле:

где r  расстояние от заряда до точки электрического поля.

Принцип суперпозиции (для потенциала): потенциал поля системы зарядов равен алгебраической сумме потенциалов полей каждого из зарядов в данной точке.

 = ₁ + ₂ +. . . + _n

Работа электростатического поля по перемещению заряда равна произведению величины перемещаемого заряда q на разность потенциалов в начальном ₁ и конечном ₂ положениях заряда:

A = q(₁ – ₂).

Следствие: работа электростатического поля по замкнутой траектории равна нулю, так как в этом случае

Работу электростатического поля также вычисляется по формуле:

A = qEr cos,

где r — перемещение заряда;  — угол между направлением вектора напряженности электрического поля и направлением перемещения заряда.

Диэлектрики — вещества, в которых нет свободных зарядов. Поэтому диэлектрики не проводят электрический ток.

Если диэлектрик поместить во внешнее электрическое поле, то напряженность поля внутри диэлектрика будет меньше, чем в вакууме.

Диэлектрическая проницаемость среды  показывает, во сколько раз напряженность поля в вакууме Е₀ больше напряженности поля в данной среде Е:

В диэлектрике кулоновская сила, напряженность и потенциал поля уменьшаются в  раз:

Проводники — вещества, имеющие свободные электрические заряды и способные проводить электрический ток.

Напряженность электрического поля в проводнике равна нулю Е = 0, а потенциал поля постоянен  = const.

Электрическая емкость С (Ф) равна отношению заряда проводника q к потенциалу проводника  :

Электроемкость зависит от геометрической формы и размеров проводника и от диэлектрической проницаемости среды, в которой находится проводник.

Конденсатор состоит из двух проводников — обкладок, заряженных разноименными и равными по абсолютной величине зарядами.

Емкость конденсатора

,

где q— заряд на обкладке, U = ₁ - ₂ — напряжение на обкладках конденсатора.

Плоский конденсатор состоит из двух плоских параллельных пластин, между которыми находится диэлектрик.

Емкость плоского конденсатора определяется по формуле:

где d - расстояние между пластинами, S - площадь пластины, ₀ - электрическая постоянная,  - диэлектрическая проницаемость среды в конденсаторе.

Емкость сферического конденсатора определяется по формуле:

C = 4₀R,

где R — радиус конденсатора.

Энергия W электрического поля конденсатора:

где С - емкость конденсатора, U – напряжение (разность потенциалов) между пластинами, q - заряд на пластине.

Соединения конденсаторов (рис. 12, рис. 13):

Рис. 12 Последовательное соединение			Рис. 13 Параллельное соединение