УКРАЇНА

ДЕРЖАВНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД

КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ

ІМЕНІ ВАДИМА ГЕТЬМАНА

Факультет економіки та управління

Кафедра макроекономіки і державного управління

ЗВІТ ПО ЗАДАЧІ № 3

Підготували:

студ. гр. ЕМД-406

ФЕтаУ

Ковальчук Юлія

Лось Валерій

Пасічник Анатолій

Халабов Юрій

Рецензент:

д.ек.н., доц. Ємельяненко

Лариса Михайлівна

КИЇВ 2013

№ 3. Експорт країни В за 1980—2000 рр. характеризуються даними, поданими в табл. 2.2.

Таблиця 2.2

Рік	Країна В, млн грн
	Експорт
1980	1065
1981	1266
1982	1474
1983	1540
1984	1798
1985	2026
1986	2286
1987	2640
1988	2924
1989	3337
1990	3479
1991	3367
1992	3477
1993	3900
1994	4498
1995	4660
1996	4846
1997	4980
1998	5012
1999	5491
2000	5764

Завдання:

1) За даним рядом побудуйте графік динаміки.

2) Розрахуйте показники динаміки та статистичні характеристики часового ряду.

3) Перевірте наявність тренду у часовому ряді, використовуючи метод різниць середніх рівнів.

4) Перевірте наявність тренду у часовому ряді, використовуючи метод Форстера—Стьюарта.

Завдання 1

За допомогою MS Excel було побудовано графік динаміки експорту країни В за 1980-2000рр., який набув вигляду:

З даного графіку ми бачимо, що ряд є нестаціонарним, а отже може мати тренд.

Також з графіка випливає наявність висхідної тенденції, з якої випадає лише декілька точок (1991-1993рр), що може свідчити про наявність випадкової компоненти в середині ряду.

Середній обсяг експорту за 1980-2000 рр. – 3325 млн. грн. В середньому цей показний щороку змінювався на 1443,6 млн. грн.

Середній абсолютний приріст за розрахунковий період склав – 223,8 млн. грн. Слід звернути увагу на 1991р., коли обсяги експорту скоротились на 112 млн грн. або на 3,22% (це було пов’язано із розпадом загальногосподарської системи СРСР і, як наслідок, загальним спадом виробництва та втратою зовнішньоекономічних зв’язків і канали збуту продукції), і 1994р, коли експорт зріс на 598 млн грн., або на 15,3 % (основні причини – подолання політичної кризи та фінансової криз, відновлення внутрішнього виробництва та зовнішньоекономічних зв’язків, внаслідок чого експорт зріс).

Завдання 2

Було розраховано такі показники динаміки часового ряду: Абсолютний ланцюговий приріст, Темп зростання, %, Темп приросту, %.

Абсолютний ланцюговий приріст розрахуємо за формулою: Δy_t=y_t-y_t-1.

Зі знайдених значень ми бачимо, що всі вони додатні, окрім -112 (за 1991р.). Це свідчить про наявність висхідного тренду і випадкової компоненти в середині ряду.

Темп зростання (%) розрахуємо за формулою: T_t(зр)=(y_t/y_t-k)*100%.

Знайдені значення у всіх роках, крім 1991, єбільшими за 100%, що підтверджує нашу гіпотезу про наявність тренду і випадкової компоненти в середині ряду.

Темп приросту (%) розрахуємо за формулою: T_t(пр)=T_t(зр)-100%.

Даний показник є додатнім у всіх роках крім 1991, що свідчить про наявність додатнього тренду і випадкової компоненти в середині ряду.

Завдання 3

Перевіримо наявність тренду у часовому ряді, використовуючи метод різниць середніх рівнів.

1. Вихідний часовий ряд (1980-2000 рр.) розподіляємо на дві рівні частини: n1=10 і n2=11 років (n1+n2=n).

Рік	Експорт				Рік	Експорт
1980	1065				1990	3479
1981	1266				1991	3367
1982	1474				1992	3477
1983	1540				1993	3900
1984	1798				1994	4498
1985	2026				1995	4660
1986	2286				1996	4846
1987	2640				1997	4980
1988	2924				1998	5012
1989	3337				1999	5491
					2000	5764

2. Розрахуємо середні значення і дисперсії для цих частин за формулами:

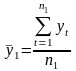= 2035,6

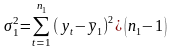= 562533,8222

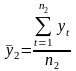= 4497,636364

= 695023,8545

3. Перевіримо однорідність дисперсій обох частин ряду.

Розрахуємо F-критерій Фішера. Оскільки Ϭ ²₂> Ϭ²₁, то F= Ϭ ²₂/Ϭ²₁.

F= 695023,8545: 562533,8222= 1,235523674.

Порівняємо розрахункове значення із табличним значенням критерію Фішера F_α на рівні значущості α=0,05 із числом рівнів свободи k₁=n₁-1=9, k₂=n₂-1=10.

k1 k2	1	2	3	4	5	6	7	8	9	10	15
10	4.96	4.10	3.71	3.48	3.33	3.22	3.14	3.07	3.02	2.98	2.85

F_α = 3,02

F=1,24

F< F_α, 1,24<3,02 – тому приймаємо гіпотезу про рівність дисперсій і переходимо до четвертого кроку.