3.1 Кинематический расчет

Исходные данные:

Угол поворота выходного вала, α,  500

Время поворота, t, с 1

Момент сопротивления, М_с, Н∙м 0,1

Требуемая мощность на выходе:

Р_вых = М_с·ω,

где – угловая скорость выходного вала.

8,72 рад/с.

Р_вых = 0,1·8,72 = 0,87 Вт.

Так как структура механизма пока неизвестна, условно примем его КПД = 0,5. Тогда мощность электродвигателя:

Р_дв = Р_вых/КПД = 0,87/0,5 = 1,74 Вт.

Выбираем электродвигатель МН-145А с выходной мощностью Р_дв = 2,45 Вт, крутящим моментом М_дв = 0,165 Н∙м и скоростью вращения вала ω_дв = 145 об/мин = 15,18 рад/с [1]¹.

Передаточное отношение механизма:

u = ω_дв/ω = 15,18/8,72 = 1,74

Такое передаточное отношение обеспечивается одноступенчатой цилиндрической зубчатой передачей. Число зубьев входного колеса z₁ = 20, выходного z₂ = z₁·u = 20·1,74 = 34,8. Число z₂ не целое, что невозможно. Выбираем z₂ = 35, при этом u = 1,75. Погрешность передаточного отношения 0,6% от 500 или 3, что будет учтено при расчете на точность.

Структурная схема механизма показана на рисунке 1, кинематическая – на рисунке 2.

Функция преобразования:

.

Рисунок 1 – Структурная схема механизма

Рисунок 2 – Кинематическая схема механизма

3.2 Силовой расчет

Выполним расчет зубчатой передачи в соответствии с [2]².

Зубчатая передача является закрытой и работает со смазкой, поэтому основным является расчет межосевого расстояния из условия контактной прочности зубьев:

,

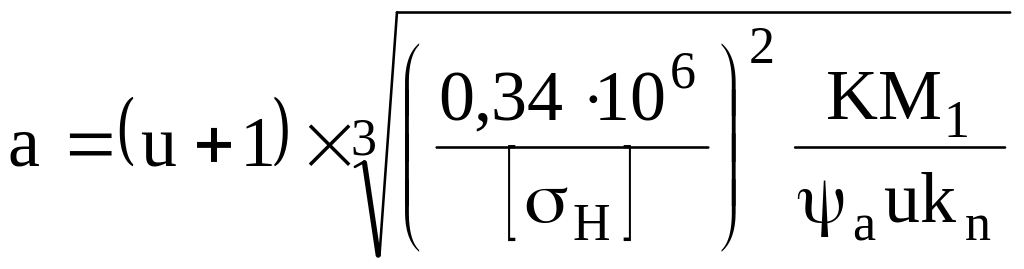где u = u_p = 1,75 – передаточное отношение редуктора; [_H] – допускаемые контактные напряжения, для улучшенных колес из стали 40Х [_H] = 770 МПа; К – коэффициент нагрузки, с учетом консольного расположения звездочек цепной передачи на валах редуктора К = 1,5; М₁ – момент на шестерне, М₁ = М_с = 0,1 Нм; _а – коэффициент ширины колеса, для прямозубых колес _а = 0,3; k_n – коэффициент, учитывающий суммарную длину контактных линий, для прямозубых колес k_n = 1.

Расчетное значение межосевого расстояния:

м = 10,5 мм

Округляем расчетное значение до ближайшего большего стандартного а = 12 мм.

Модуль зубчатой передачи m = 2a/(z₁ + z₂)  = 2·12/(20 + 35)  0,44 мм.

Округляем расчетное значение до ближайшего большего стандартного m = 0,5 мм.

Уточненное значение межосевого расстояния a = 0,5m(z₁ + z₂) = 13,75 мм.

Проверим передачу на изгиб зубьев. Напряжения изгиба:

,

где  – коэффициент износа, для закрытых передач  = 1; Y – коэффициент формы зуба, для z₁ = 20 Y = 0,372; B – ширина зубчатого колеса, В = a·_а = 13,75·0,3  5 мм.

В результате получаем:

21,510⁶ Па

Допустимое значение [_и] определяется по формуле:

,

где _–1 – предел выносливости при изгибе, для стали 40Х _–1 = 455 МПа; k_р – коэффициент режима нагрузки, при неравномерной нагрузке k_р = 1,5; [n] – требуемый коэффициент запаса прочности, [n] = 1,5; k_ – коэффициент концентрации напряжений, k_ = 1,5.

МПа

Расчетное значение напряжений 21,5 МПа меньше допустимого 455 МПа, следовательно изгибная прочность зубьев обеспечивается.

3.3  Расчет на точность

Расчет погрешности механизма выполняется по методу максимума-минимума. Ориентировочно примем 8-ю степень точности зубчатых колес.

В соответствии с [3]³ максимальное значение кинематической погрешности зубчатой передачи:

,

где и – допуски на кинематические погрешности ведущего и ведомого колес, по ГОСТ1643 для 8-й степени точности мкм, мкм; К – коэффициент фазовой компенсации, по таблице [3] К = 0,85; и – погрешности монтажа зубчатых колес; так как ведущее колесо нарезано непосредственно на валу , для ведомого колеса:

,

где e_r и e_a – допуски на радиальное и торцовое биения посадочного диаметра и заплечика для установки зубчатого колеса на валу; α – угол исходного профиля колеса. В соответствии с [4, с. 209, 210]⁴ для степени точности 6 расположения поверхностей и посадочного диаметра 10 мм (диаметр заплечика 12 мм) e_r = 10 мкм, e_a = 5 мкм.

мкм.

= 100,5 мкм

Максимальное значение мертвого хода в передаче:

,

где E_Hs1 и E_Hs2 – наименьшее смещение исходного контура ведущего и ведомого колес, по ГОСТ1643 для 8-й степени точности E_Hs1 = 90 мкм и E_Hs2 = 90 мкм; Т_Н1 и Т_Н2 – допуски на смещение исходного контура ведущего и ведомого колес, по ГОСТ1643 для 8-й степени точности Т_H1 = 95 мкм и Т_H2 = 95 мкм; f_a – допуск на межосевое расстояние в передаче, по ГОСТ1643 для 8-й степени точности f_a = 35 мкм; G_r1 и G_r2 – то же, что и и , то есть погрешности монтажа зубчатых колес, G_r1 = 0, G_r2 =   = 5,3 мкм.

= 176,7 мкм.

Общая погрешность 100,5 + 176,7 = 277,2 мкм.

Переведем значение погрешности в угловые единицы (d – делительный диаметр ведомого колеса):

= 149’.

С учетом погрешности передаточного отношения, полученной в кинематическом расчете и равной 3, общая погрешность составит 449’. По заданию допустимая погрешность составляет 4. Так как расчетная погрешность больше допустимой, следует использовать зазоровыбирающие колеса для устранения мертвого хода. В этом случае 100,5 мкм, , и с учетом погрешности передаточного отношения < 4. Таким образом, заданная точность обеспечивается.

3.4  Расчеты типовых элементов механизма

1. Расчет выходного вала на кручение

На выходной конец вала действует момент сопротивления М_с = 0,1 Н∙м. Условие прочности вала может быть записано в виде [1]

,

где W_p – полярный момент сопротивления сечения вала, , где d_в – диаметр вала, d_в = 6 мм; [τ_к] – допускаемые напряжения для материала вала при кручении, для улучшенной стали 40X при знакопеременной нагрузке в соответствии с [5]⁵ [τ_к] = 115 МПа. Отсюда:

Па = 2,36 МПа.

Так как τ_к  = 2,36 МПа < [τ_к] = 115 МПа, прочность выходного вала обеспечивается.

3.4.2  Расчет штифтового соединения

Выполним расчет штифтового крепления зубчатого колеса на выходном валу. Эскиз соединения показан на рисунке 3. Конструктивные размеры: d_в = 10 мм, D = 15 мм. На соединение действует выходной момент сопротивления М_с = 0,1 Н∙м. Требуется рассчитать диаметр штифта.

Рисунок 3 – Эскиз штифтового соединения

Расчет штифта на срез.

Условие прочности штифта:

,

где А_ср = πd²/4 – площадь среза; [τ_ср] – допускаемые напряжения для материала штифта при срезе, [τ_ср] = 80 МПа. Отсюда:

0,56·10^–3 м = 0,56 мм.

Расчет штифта на смятие.

Условие прочности штифта:

,

где А_см = d(D – d_в) – площадь смятия; [σ_см] – допускаемые напряжения для материала штифта при смятии, [σ_см] = 200 МПа. Отсюда:

20·10^–6 м = = 0,02 мм.

По результатам расчета диаметр штифта должен быть не менее 0,56 мм. В соответствии с диаметром вала выбираем штифт диаметром 1,6 мм.

3.4.3  Выбор подшипников качения.

Так как вал двигателя имеет диаметр 6 мм, то входной вал механизма будет иметь тот же диаметр, он же является посадочным диаметром подшипников. Выходной вал для унификации установлен на подшипниках такого же размера. При крутящем моменте на выходном валу М_с = 0,1 Н∙м радиальная нагрузка на подшипники F_r = 2M_c/d₂ = 2·0,1/17,5·10^–3 = 11,43 Н. Осевая нагрузка F_a равна нулю, так как используются цилиндрические прямозубые колеса, поэтому выбираем радиальные шарикоподшипники. Скорость вращения валов больше 1 об/мин, поэтому расчет ведется по динамической грузоподъемности.

Эквивалентная динамическая нагрузка:

Р = (XVF_r + YF_a)K_бK_t,

где X и Y – коэффициенты радиальной и осевой нагрузок, для радиального подшипника X = 0,6; V – коэффициент вращения, при вращающемся внутреннем кольце и неподвижном наружном V = 1; K_б – коэффициент безопасности, для нормальных условий K_б = 1; K_t – температурный коэффициент, при нормальных температурных условиях равен 1.

В итоге получим Р = 0,6·11,43 = 6,86 Н.

Срок службы по заданию L_h = 5000 часов или в оборотах:

L = 60n L_h·10^–6, млн. об.,

где n – скорость вращения в оборотах в минуту, n = 83,3 об/мин (из кинематического расчета).

Срок службы L = 60·83,3·5000·10^–6 = 25 млн. об.

Расчетная динамическая грузоподъемность:

С_р = L^1/αP,

где α – коэффициент, зависящий от типа подшипника, для радиального подшипника α = 3.

Расчетная динамическая грузоподъемность С_р = 25^1/3·6,86 = 20 Н.

По ГОСТ 8338-75 выбираем радиальный однорядный шарикоподшипник с посадочным диаметром 6 мм и динамической грузоподъемностью больше 20 Н. Подходящий подшипник – 1000096 (наружный диаметр 15 мм, ширина 5 мм, динамическая грузоподъемность 1470 Н).

3.4.4  Расчет пружины для зазоровыбирающего зубчатого колеса [6]⁶

Для выборки зазора пружина кручения должна обеспечить крутящий момент, превышающий момент сопротивления, равный М_с = 0,1 Н∙м. Для обеспечения минимальных размеров конструкции целесообразно использовать пружину с минимальным количеством витков. При использовании пружины с одним витком требуемая жесткость определяется по формуле:

С = М_с/Ф = С’(D₁ – d)²/3,2,

где Ф – угол закручивания витка, который не должен превышать величины 1,07S₃/(D₁ – d), где S₃ – предельная деформация витка, D₁ – наружный диаметр пружины, d – диаметр проволоки.

По габаритам подходит пружина 302 ГОСТ 13766-76 (d = 1,6 мм, D₁ = 18 мм, С’ = 14,58 Н·мм, S₃ = 3,841 мм). Предельный угол закручивания:

рад = 14.

Необходимый угол закручивания:

0,0008 рад = 0,05.

Так как требуемый угол не превышает предельный, пружина подходит для разрабатываемой конструкции.