5. Линейные дифференциальные уравнения 1-го порядка.

Линейным уравнением 1-го порядка называется уравнение, линейное относительно искомой функции и ее производной. Оно имеет вид:

, (7.1)

Где P(X) И Q(X) – заданные непрерывные функции от X. Если функция , То уравнение (7.1) имеет вид: (7.2)

И называется линейным однородным уравнением, в противном случае оно называется линейным неоднородным уравнением.

Линейное однородное дифференциальное уравнение (7.2) является уравнением с разделяющимися переменными:

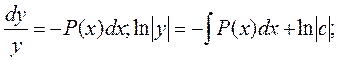
(7.3)

Выражение (7.3) есть общее решение уравнения (7.2). Чтобы найти общее решение уравнения (7.1), в котором функция P(X) обозначает ту же функцию, что и в уравнении (7.2), применим прием, называемый методом вариации произвольной постоянной и состоящий в следующем: постараемся подобрать функцию С=С(X) Так, чтобы общее решение линейного однородного уравнения (7.2) являлось бы решением неоднородного линейного уравнения (7.1). Тогда для производной функции (7.3) получим:

.

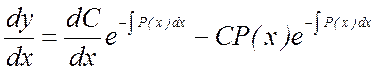Подставляя найденную производную в уравнение (7.1), будем иметь:

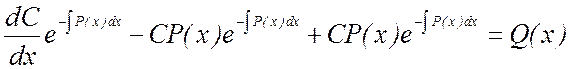
Или .

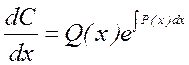Откуда , где - произвольная постоянная. В результате общее решение неоднородного линейного уравнения (7.1) будет (7.4)

Первое слагаемое в этой формуле представляет общее решение (7.3) линейного однородного дифференциального уравнения (7.2), а второе слагаемое формулы (7.4) есть частное решение линейного неоднородного уравнения (7.1), полученное из общего (7.4) при . Этот важный вывод выделим в виде теоремы.

Теорема. Если известно одно частное решение линейного неоднородного дифференциального уравнения , то все остальные решения имеют вид , где - общее решение соответствующего линейного однородного дифференциального уравнения.

Однако надо отметить, что для решения линейного неоднородного дифференциального уравнения 1-го порядка (7.1) чаще применяется другой метод, иногда называемый методом Бернулли. Будем искать решение уравнения (7.1) в виде . Тогда . Подставим найденную производную в исходное уравнение: .

Объединим, например, второе и третье слагаемые последнего выражения и вынесем функцию U(X) за скобку: 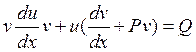(7.5)

Потребуем обращения в нуль круглой скобки: .

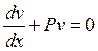Решим это уравнение, полагая произвольную постоянную C равной нулю: 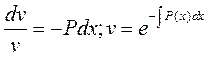. С найденной функцией V(X) вернемся в уравнение (7.5): .

Решая его, получим: .

Следовательно, общее решение уравнения (7.1) имеет вид:

.

Заключение (итог занятия):

(повторение основных положений лекции, обобщение изложенного, установление связей изложенного с последующим материалом).

Оснащение занятия:

• доска,

• раздаточный материал - учебно-методическое пособие "Дифференциальные уравнения"

Домашнее задание:

• Математика: учеб. пособие §2.2.

• Расчётно-графическая работа по теме «Применение дифференциальных уравнений первого порядка для решения задач»

Литература:

Основные источники:

1. Математика: учеб. пособие/В. П. Омельченко, Э. В. Курбатова. - Изд. 7-е, стер. - Ростов н/Д: Феникс, 2013. - 380 с. - (Среднее профессиональное образование).

Дополнительные источники:

1. Богомолов Н. В. Практические занятия по математике: учебное пособие для средних учебных заведений – 7-е издание, М.: Высшая школа, 2004

2. Гмурман В. Е. Теория вероятностей и математическая статистика: учебное пособие – 12-е изд., - М.: Издательство Юраст, 2010

3. Кочетков Е. С. Смергинская С. О., Соколов В. В. Теория вероятностей и математическая статистика – М.: Форум, 2011.

4. Пехлецкий И. Д. Математика: учебник для студентов образовательных учреждений специального профессионального образования – 3-е издание, стер. – М.: Издательский центр «Академия», 2007

Интернет страницы, сайты

1. http://www.mathpapa.com - алгебраический калькулятор

2. http://www.bymath.net – средняя математическая интернет-школа (вся элементарная математика)

3. http://www.mathematics.ru - учебный компьютерный курс по алгебре

4. http://www.mathtest.ru - ресурс предназначен для студентов с целью проверки их знаний

5. http://bim.ucoz.ru - сайт преподавателя

Преподаватель __________________________Уварчева И. Ю.