Учебно-методическая карта теоретического занятия

Специальность	060501 Сестринское дело
Тема 1.5	Дифференциальные уравнения
Тип занятия	Комбинированный
Форма проведения	Лекционно-практическое занятие изучения нового материала
Цели занятия:
Учебная:	Раскрыть сущностные основы теории дифференциальных уравнений и основных методов их решения. Научить решать типовые дифференциальные уравнения.
Развивающая:	Привить элементарные навыки моделирования простейших медико-биологических явлений с помощью дифференциальных уравнений.
Воспитательная:

Межпредметные связи: биология

Внутрипредметные связи:

Учащиеся должны иметь представление о:

• дифференциальном и интегральном исчислении;

• элементарных функциях,

• предмет и задачи информатики, её место и роль в деятельности человека, живой природе и в медицине;

Учащиеся должны знать:

• определение дифференциального уравнения,

• определение функции,

• определение предела функции,

• свойства пределов функции.

Изучаемые вопросы:

• Понятие дифференциального уравнения и его решения

• Методы решения уравнений с разделяющимися переменными.

• Методы решения линейных дифференциальных уравнений.

• Примеры решения дифференциальных уравнений, описывающих медико-биологические процессы

План и содержание занятия (структура занятия)

1. Организационная часть (проверка присутствующих, готовность обучающихся к занятию, наличие формы и т.д.)

Введение

Дифференциальные уравнения занимают особое место в математике и используются во многих науках. Исследование природных явлений и изучение закономерностей общественных процессов приводит к построению математических моделей, основу которых составляют дифференциальные уравнения.

В дифференциальных уравнениях неизвестная функция содержится вместе со своими производными. Главная задача теории дифференциальных уравнений – изучение функций, представляющих собой решение этих уравнений.

Мы рассмотрим элементы теории обыкновенных дифференциальных уравнений (неизвестные функции зависят от одной переменной).

2. Основная часть (70 мин)

3. Итог занятия. (10 мин) содержание теоретического материала

1. Дифференциальные уравнения, их порядок и степень

Дифференциальным уравнением называется такое уравнение, которое содержит производные или дифференциалы неизвестной функции.

Порядком дифференциального уравнения называется порядок наивысшей производной, содержащейся в нём.

Определение 1. Обыкновенным дифференциальным уравнением N – го порядка для функции Y Аргумента X Называется соотношение вида

(1.1),

Где F – заданная функция своих аргументов. В названии этого класса математических уравнений термин «дифференциальное» подчеркивает, что в них входят производные (функции, образованные как результат дифференцирования); термин – «обыкновенное» говорит о том, что искомая функция зависит только от одного действительного аргумента.

Обыкновенное дифференциальное уравнение может не содержать в явном виде аргумент X, Искомую функцию и любые ее производные, но старшая производная обязана входить в уравнение N-Го порядка. Например

А) – уравнение первого порядка;

Б) – уравнение третьего порядка.

При написании обыкновенных дифференциальных уравнений часто используются обозначения производных через дифференциалы:

В) 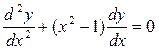– уравнение второго порядка;

Г) – уравнение первого порядка,

Образующее после деления на Dx эквивалентную форму задания уравнения: .

Функция называется решением обыкновенного дифференциального уравнения, если при подстановке в него оно обращается в тождество.

Например, уравнение 3-го порядка

имеет решение .

Найти тем или иным приемом, например, подбором, одну функцию, удовлетворяющую уравнению, не означает решить его. Решить обыкновенное дифференциальное уравнение – значит найти Все функции, образующие при подстановке в уравнение тождество. Для уравнения (1.1) семейство таких функций образуется с помощью произвольных постоянных и называется общим решением обыкновенного дифференциального уравнения N-го порядка, причем число констант совпадает с порядком уравнения: Общее решение может быть, и не разрешено явно относительно Y(X): В этом случае решение принято называть общим интегралом уравнения (1.1).

Например, общим решением дифференциального уравнения является следующее выражение: , причем второе слагаемое может быть записано и как , так как произвольная постоянная , делённая на 2, может быть заменена новой произвольной постоянной .

Задавая некоторые допустимые значения всем произвольным постоянным в общем решении или в общем интеграле, получаем определенную функцию, уже не содержащую произвольных констант. Эта функция называется частным решением или частным интегралом уравнения (1.1). Для отыскания значений произвольных постоянных, а следовательно, и частного решения, используются различные дополнительные условия к уравнению (1.1). Например, могут быть заданы так называемые начальные условия при (1.2)

В правых частях начальных условий (1.2) заданы числовые значения функции и производных, причем, общее число начальных условий равно числу определяемых произвольных констант.

Задача отыскания частного решения уравнения (1.1) по начальным условиям называется задачей Коши.