IV Выводы

Контрольные вопросы:

1. Закон сохранения механической энергии для поступательного движения.

2. Кинетические характеристики поступательного в вращательного движения.

3. Написать две формы основного уравнения динамики вращательного движения.

4. Закон сохранения энергии для движения цилиндра по наклонной плоскости.

5. Физический смысл момента инерции. Теорема Штейнера.

Литература.

1. Руководство к лабораторным занятиям по физике / Под ред.

Л.Л. Гольдина. - М., 1973.

2. Трофимова Т.И. Курс физики / Т.И. Трофимова / Учебное пособие для вузов. – 3-е изд. , М.: Высш. шк., 2000. – 478 с.

3. Айзенцон А.Е. Курс физики / А.Е. Айзенцон – М.: Высш. шк., 1996.

– 457 с.

4. Яворский Б.М. , Детлаф А.А. Справочник по физике / Б.М. Яворский, А.А. Детлаф, М.: Наука, 1979. – 942 с.

ЛАБОРАТОРНАЯ РАБОТА № 2

«Определение ускорения свободного падения методом математического маятника»

Цель работы: опытным путем определить ускорения свободного падения в данном месте и сравнить его со средним ускорением свободного падения Земли.

Приборы и оборудование: кронштейн, шарик на нити, линейка, секундомер.

Схема установки

Рисунок 1 – Установка для определения ускорения свободного падения методом математического маятника

Элементы схемы: 1. кронштейн; 2. нить; 3. металлический шарик.

I Теоретическая часть и расчётная часть

Математический маятник – материальная точка, подвешенная на невесомой нерастяжимой нити. Моделью материальной точки является, обладающий центрально-сферической симметрией метал­лический шарик. Экспериментально периоды колебаний маятников определяются по формулам:

Применение маятников максимально длинной и максимально короткой нити позволяет уменьшить погрешности измерений периода колебаний, так как

ΔТ~ .

Вывод расчётной формулы.

Из формул периодов колебаний математических маятников:

После возведения этих формул в квадрат и вычитания имеем:

,

выражая отсюда ускорение свободного падения g получаем расчётную формулу:

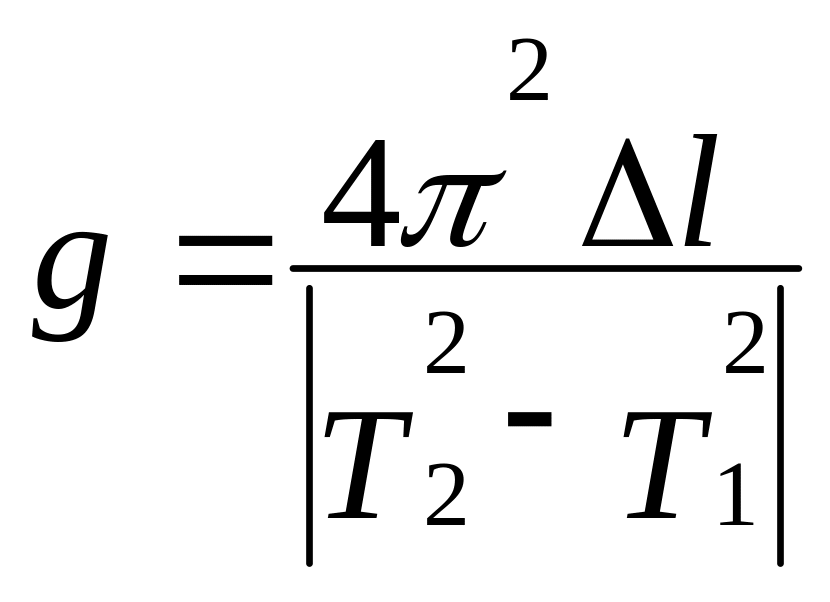
где

Расчётные формулы

1. Определение среднего значения 3-х измерений максимально длиной нити.

2.Расчёт среднего времени 3-х измерений максимально длиной нити.

3 . Период колебаний длиной нити.

4. Определение средней длины максимально короткой нити.

5. Расчёт среднего времени 3-х измерений максимально короткой нити.

6. Период колебаний длиной нити.

Результаты подставить в расчётную формулу:

.

II Методика проведения работы

1.Подвесить шарик на максимально длинной нити.

2.Произвести линейкой измерения длины нити.

3.Секундомером измерить время 10-ти колебаний.

4. Подвесить шарик на максимально короткой нити.

5. Произвести линейкой измерения длины нити.

6. Секундомером измерить время 10-ти колебаний.

7. Рассчитать по формуле(*) ускорение свободного падения в данном месте.

8. Экспериментальные и расчётные данные занести в таблицу.

9. Произвести оценку погрешностей.

III Таблица 1 – Экспериментальные и расчетные данные.

№	l1, м	l2, м	t1, с	t2, с	N	T1, c	T2, c	go, м/с2	g, м/с2
1					10			9,81
2
3

IV Оценка погрешности измерений:

А бсолютная погрешность: ∆g = |g – g_o|

Относительная погрешность: ε = (∆g /g_o) ∙ּ 100%