Ізотропна дифракція світла, на акустичних хвилях

Явище дифракції світла на ультразвуковій хвилі було передбачене Бриллюеном в 1922 р, а експериментально здійснене в 1932 р Дебаєм і Сірсом. В 1935-36 рр. Раман і Нат розробили теорію дифракції, в якій зроблено припущення, що звуковий пучок подібний до двомірної фазової гратки, при взаємодії з якою напрями світлових променів не змінюються. При такому підході розподіл інтенсивності променів не змінюється, а розподіл інтенсивності світла по дифракційним максимумам описується функціями Бесселя. Послідуючі дослідження показали, що ця теорія може бути застосована тільки для дуже вузьких ультразвукових пучків. В послідуючих працях Раман і Нат відмовились від моделі простої фазової гратки. Ними була знайдена нескінчена система зв’язаних дифрівнянь, які описують особливу просторову поведінку різних дифракційних порядків.

Фізична картина світла на пружній хвилі може описуватися таким чином. Поширення акустичної хвилі в пружнооптичному середовищі супроводжується появою в цьому середовищі біжучої періодичної послідовності змін показника заломлення. Якщо період цієї послідовності менший за ширину світлового пучка, то в середовищі відбувається дифракція світла на біжучій з швидкістю звука фазовій дифракційній гратці. Характер цієї дифракції істотно залежить від довжини області взаємодії світла і звуку l. При досить малому l дифракційна гратка може розглядатись як плоска. У цьому випадку напрями на дифракційні максимуми визначаються, як у звичайній дифракційній гратці:

, (26)

де _m – напрям на m-й дифракційний максимум (m = 0,1,…), _о – кут падіння світла.

при досить малому l дифракційна картина являє собою набір значного числа дифракційних максимумів, розміщених симетрично відносно напряму падаючого світла. така дифракція називається дифракцією Рамана-Ната, і відбувається вона при будь-якому куті падіння світла на ультразвуковий стовп. При дифракції Рамана-Ната можна вважати, що світловий промінь проходить через область взаємодії прямолінійно. Знехтування викривленням променя всередині області взаємодії еквівалентно допущенню про чисто фазову модуляцію світла при його взаємодії з пружною хвилею. Розглядаючи модульовану по фазі хвилю на виході із області взаємодії в просторово-кутовий спектр, можна отримати характерну для дифракції Рамана-Ната картину з великим числом дифракційних максимумів (рис.4,а) .

Цілком інший характер має дифракція світла на ультразвуці при великому l. дифракційна гратка у цьому випадку є тривимірною, і при аналізі дифракційної картини необхідно врахувати фазові співвідношення між хвилями різних дифракційних максимумів. Характер дифракції світла на ультразвуковій хвилі з великим l подібний до дифракції рентгенівських променів на кристалічній структурі. Така дифракція відбувається тільки при певному куті падіння світла на ультразвуковий стовп, який задовольняє так званій умові Вульфа-Брегга. Цей режим дифракції носить назву дифракції Брегга. Для нього характерно наявність тільки одного бокового дифракційного максимуму.

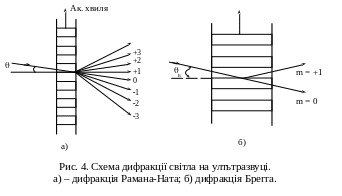
Режим дифракції Рамана-Ната і Брегга являють собою два граничних випадки, які відповідають малій і великій довжині області взаємодії світла і звуку. Плавний перехід між цими режимами відбувається при неперервній зміні l. Таким чином, по мірі збільшення l відбувається зменшення числа дифракційних максимумів і звуження допустимих граничних кутів падіння світла. Строгі межі режимів дифракції не можуть бути установлені по тій причині, що число дифракційних максимумів істотно залежить від потужності ультразвукової хвилі, з її збільшенням число дифракційних максимумів зростає.

Акустична хвилі створює в середовищі періодичний у просторі розподіл показника заломлення. Промінь світла при своєму поширенні в такому середовищі дифрагує на неоднорідностях n. Утворюється ряд максимумів випромінювання з різними напрямами світлового вектора (рис.4,а).

Хоча сумарна інтенсивність по всім максимумам стала і дорівнює інтенсивності падаючого світла, розподіл енергії по максимумам залежить від інтенсивності акустичної хвилі, що і дає можливість модулювати світло в кожному окремому максимумі.

Розглянемо коротко теорію модуляції світла при його дифракції на акустичній хвилі. В найбільш простій формі вона розвинута в працях Рамана і Наата.

Нехай світловий пучок падає на границю прозорого середовища, в якому збуджені акустичні хвилі. Напрям поширення цих хвиль перпендикулярний до променя світла (рис.5). Якщо ширина акустичного стовпа у напрямі поширення світла l достатньо мала, то можна вважати, що світлові промені проходять через акустичний стовпчик прямолінійно (це основне припущення теорії Рамана і Ната). У цьому наближенні оптична неоднорідність середовища, зв’язана із зміною показника заломлення, яка викликається акустичною хвилею, впливає тільки на фазу світла , що проходить акустичний стовпчик. Таким чином, світлове поле в площині x = l модульоване тільки по фазі, але стан по амплітуді.

Швидкість поширення світла і акустичної хвилі в середовищі відрізняється приблизно на шість порядків, тому за час проходження світла через акустичний стовпчик останній можна вважати нерухомим. Увівши таке припущення, можемо розрахувати дифракційну картину при довільному миттєвому значенні акустичного поля, а потім врахувати залежність цього поля від часу. Дифракційна картина буде слідувати практично без відставання за зміною пружних напруг.

Якщо на вході модулятора (при х = 0) світлова хвиля має плоский фронт з амплітудою Е_о, то при x = l у випадку стоячої акустичної хвилі:

, (27)

а у випадку біжучої хвилі:

, (28)

де

, ,

n – амплітуда зміни показника заломлення під дією акустичної хвилі. По відомому полю в площині x = l можна знайти поле в будь-якій точці простору x  l. Викликає інтерес поле в дальній зоні, на відстанях, більших у порівнянні з розмірами модулюючої комірки. Діаграма напрямленості випромінювання описується наступним інтегралом:

, (29)

де b i L – поперечні розміри дифракційної гратки, а  - кут спостереження.

Підставляючи в цей інтеграл значення Е_х=l із () і () отримаємо у випадку біжучої акустичної хвилі:

(30)

і у випадку стоячої акустичної хвилі:

, (31)

де J_m – функція Бесселя m-го порядку.

Звідси знаходимо напрями дифракційних максимумів

(32)

Вирази (30) і (31) визначають інтенсивності і частоти дифракційних максимумів різних порядків. У випадку біжучої акустичної хвилі інтенсивність світла в m-му дифракційному максимумі пропорційна квадрату функції Бессселя m-го порядку:

, (33)

де .

Таким чином, при сталому n інтенсивності усіх максимумів незмінні у часі. Частота ж m-го максимуму рівна  + m, тобто зсунута відносно частоти вихідного світла. відсутність амплітудної модуляції світла і зсув його частоти пов’язаний з тим, що біжуча акустична хвиля створює для світла рухому фазову дифракційну гратку.

Величина аргументу функції Бесселя _о в (), яка визначає інтенсивність дифракційних максимумів, пропорційна пружній деформації u. Для біжучої акустичної хвилі існує наступний взаємозв’язок між деформацією і акустичною потужністю Р_а:

, (34)

де S – площа поперечного перерізу акустичного стовпчика,  - густина середовища,  - швидкість поширення звуку в середовищі.

Підставляючи у вираз для _о значення u із (34), отримаємо:

. (35)

При малих _о інтенсивність світла в першому дифракційному максимумі може бути записана у вигляді:

. (36)

Таким чином, ефективність фотопружного матеріалу характеризується величиною:

. (37)

яка називається акустичним коефіцієнтом якості.

Необхідно відмітити, що показник заломлення (n), складова пружнооптичного тензора (р) і швидкість звуку (), які входять у формулу (32) являються тензорними величинами, а значить, значення цих параметрів залежить від орієнтації кристалу. тому орієнтація кристалу, який використовують як активний елемент акустиоптичного пристрою, повинна відповідати максимальному значенню коефіцієнта якості.

У випадку акустичної хвилі інтенсивність m-го дифракційного максимуму пропорційна квадрату функції Беселя m-го порядку з аргументом, який залежить від часу:

. (38)

Найбільший інтерес представляє основний максимум, інтенсивність якого пропорційна функції . Виконавши спектральний аналіз цього виразу, можна отримати:

+

+ … (39)

Таким чином, інтенсивність світла, яке поширюється в напрямку  = 0, модульована частотою 2 і її гармоніками. Поява амплітудної модуляції при деформації світла на стоячій акустичній хвилі пов’язана з тим, що стояча хвиля еквівалентна нерухомій фазовій гратці із змінною у часі величиною n. Двічі за період модулюючого коливання енергії світла перекачується із основного максимуму в бокові, створюючи амплітудну модуляцію кожного із максимумів.