Өз бетінше орындауға арналған есептер
Фирма қызметтердің табыс ақының (мын. тенге), жұмыс істеген жылдардаң және жынысынаң тәуелділігі оқып алынды. 15 адамдағы таңдама келесі нәтижелерді берді:
Табыс ақысы (Y) |
84 |
88 |
63 |
65 |
95 |
75 |
87 |
67 |
85 |
70 |
92 |
62 |
86 |
64 |
91 |
Жұмыс істеген жылдары (X) |
5 |
6 |
3 |
4 |
8 |
10 |
6 |
5 |
6 |
8 |
8 |
2 |
6 |
4 |
7 |
Жынысы (Z) |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
Мұнда
,
егер қызметкер еркек
жынысы болса және
егер қызметкер әйел жынысы
болса.
ANCOVA-моделін құрып, корреляция индексін есептеңіз. Алынған нәтижелерді түсіндіріңіз.
9 Тақырып. Сызықты емес регрессия және корреляция.
Мысал. Әр түрлі шаруашылықтармен берілген тыңайтқыштар мен осы жағдайда алынған өнім көлемі белгілі болсын. Кестеде Х – тыңайтқыш (удобрение) мөлшері (кг/га) және У - өнімділік (урожайность) (ц/га) берілген.
Х |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
У |
3 |
4 |
6 |
7 |
5 |
1 |
2 |
Регрессия сызықтарының теңдеулерін құрыңыз:
а) Екі дәрежелі параболаны;
б) Тең бүйірлі гиперболаны.
Корреляция индексі бойынша Х және У факторлары арасындағы тығыздықты бағалаңыз.
Шешуі.
а) Екінші
ретті параболаның
регрессия теңдеуін
келесі түрде іздейміз:
.
Параболаның регрессия теңдеуінің коэффициенттерін табу үшін нормалдық (қалыпты)теңдеулер жүйесі мынадай болады:
Есептеуші кесте құрамыз:
№ |
|
|
|
|
|
|
|
1 |
1 |
3 |
1 |
1 |
1 |
3 |
3 |
2 |
2 |
4 |
4 |
8 |
16 |
8 |
16 |
3 |
3 |
6 |
9 |
27 |
81 |
18 |
54 |
4 |
4 |
7 |
16 |
64 |
256 |
28 |
112 |
5 |
5 |
5 |
25 |
125 |
625 |
25 |
125 |
6 |
6 |
1 |
36 |
216 |
1296 |
6 |
36 |
7 |
7 |
2 |
49 |
343 |
2401 |
14 |
98 |
Σ |
28 |
28 |
140 |
784 |
4676 |
102 |
444 |
Нәтижесінде нормалдық теңдеулер жүйесі мына түрде болады:
Крамер әдісін қолданып, теңдеулер жүйесін шешеміз:
,
,
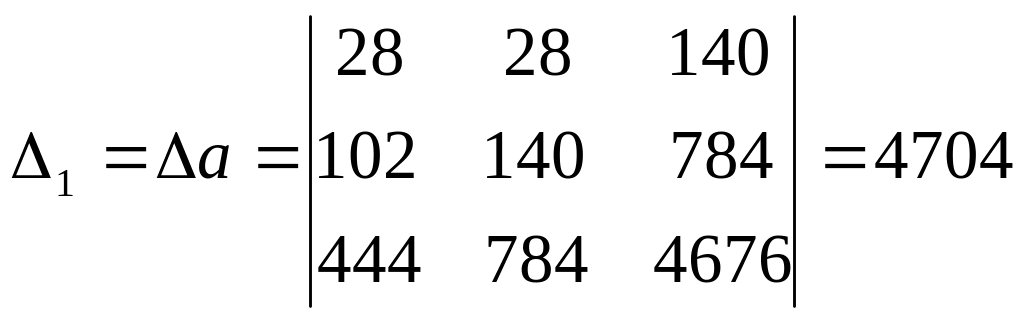
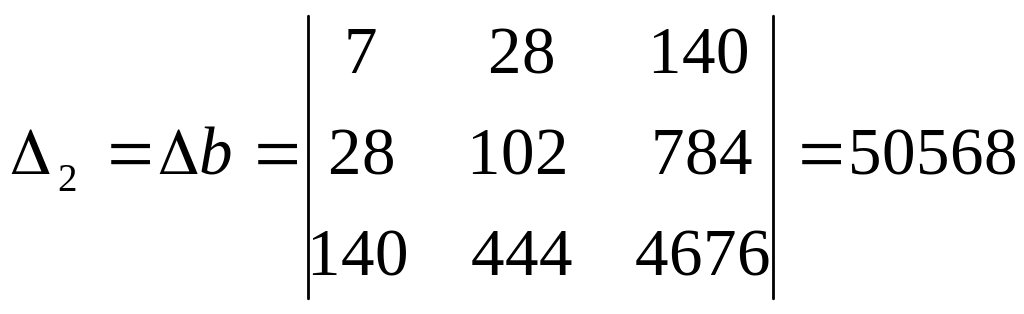Онда
,
,
Регрессия теңдеуінін келесі
түрін аламыз:
Х және У факторлар арасындағы тығыздық қатынасын табу үшін корреляция индексі R – ді табамыз.
Корреляция индексін анықтау үшін, есептеуші кестені құрамыз:
№ |
|
|
|
|
|
|
|
1 |
1 |
3 |
2,9285 |
0,0715 |
0,0051 |
-1 |
1 |
2 |
2 |
4 |
4,7141 |
-0,7141 |
0,5099 |
0 |
0 |
3 |
3 |
6 |
5,6425 |
0,3575 |
0,1278 |
2 |
4 |
4 |
4 |
7 |
5,7137 |
1,2863 |
1,6546 |
3 |
9 |
5 |
5 |
5 |
4,9277 |
0,0723 |
0,0052 |
1 |
1 |
6 |
6 |
1 |
3,2845 |
-2,2845 |
5,2189 |
-3 |
9 |
7 |
7 |
2 |
0,7841 |
1,2159 |
1,4784 |
-2 |
4 |
Σ |
28 |
28 |
|
|
8,9999 |
|
28 |
Мұндағы
-
айнымалы х-тін барлық мәндерін алып
теңдеуге қойғанда, шыққан мәндері. Ал
у-тін орта мәнін мына формуладан
анықтаймыз:
Корреляция индексін келесі
формула бойынша анықтаймыз:
Корреляция индексі R=0,8238 тең болды, бұдан мына қорытындыны шығаруға болады:
х және у арасындағы байланыс тығыз.
б) Тең бүйірлі гиперболаның регрессия теңдеуін келесі түрде іздейміз:
Тең бүйірлі гиперболаның регрессия теңдеуінің коэффициенттерін табу үшін, келесі нормалдық теңдеулер жүйесін аламыз:
Есептеуші кестені құрамыз:
№ |
|
|
|
|
|
|
1 |
1 |
3 |
1 |
1 |
1 |
3 |
2 |
2 |
4 |
0,5 |
4 |
0,25 |
2 |
3 |
3 |
6 |
0,3333 |
9 |
0,1111 |
2 |
4 |
4 |
7 |
0,25 |
16 |
0,0625 |
1,75 |
5 |
5 |
5 |
0,2 |
25 |
0,04 |
1 |
6 |
6 |
1 |
0,1667 |
36 |
0,0278 |
0,1667 |
7 |
7 |
2 |
0,1429 |
49 |
0,0204 |
0,2857 |
Σ |
28 |
28 |
2,5929 |
|
1,5118 |
10,2024 |
Біздің жағдайда келесі жұйені аламыз:
Крамер әдісін пайдаланып, теңдеулер жүйесін шешеміз:
,
Онда
,
.
Келесі регрессия теңдеуі
шығады:
.
Корреляция индексі жоғарыдағы (а-пунктіндегі)- дей анықталады. Есептеуші кестені құрамыз:
№ |
|
|
|
|
|
|
|
1 |
1 |
3 |
3,8066 |
-0,8066 |
0,6506 |
-1 |
1 |
2 |
2 |
4 |
3,9602 |
0,0398 |
0,0016 |
0 |
0 |
3 |
3 |
6 |
4,0114 |
1,9886 |
3,9545 |
2 |
4 |
4 |
4 |
7 |
4,037 |
2,963 |
8,7794 |
3 |
9 |
5 |
5 |
5 |
4,0524 |
0,9476 |
0,898 |
1 |
1 |
6 |
6 |
1 |
4,0626 |
-3,0626 |
9,3795 |
-3 |
9 |
7 |
7 |
2 |
4,0699 |
-2,0699 |
4,2845 |
-2 |
4 |
Σ |
28 |
28 |
|
|
27,9481 |
|
28 |
Енді корреляция индексін
табамыз:
,
бұдан мына қорытынды шығарамыз: х және
у арасындағы байланыс әлсіз
немесе байланыс
жоқ деп те айтуға болады.
Сонымен, негізгі мәліметтер параболалық функциямен жеткілікті жақсы жуықталады, ал гиперболамен өте жаман сипатталады.