Өз бетінше орындауға арналған есептер

1) Бір тұрғын басына у (кг) кететін жылдық ет өлшемі, бір тұрғынның жылдық табысы х₁ (мың тг) және жылдық балық өнімін тұтыну х₂ (кг) негізінде 30 аймақ бойынша деректер жасалды:

Керек қылу:

1. Жиынтық сызықтық регрессия теңдеуін құрыңыз.

2. Жиынтық корреляция коэффициентін табыңыз.

Қорытынды жасаңыз.

2) Аймақтың 10 кәсіпорны бойынша жұмыс барысында жанға негізгі фондтарды (жылдық аяғындағы фонд х₁ құнынан %) және жалпы жұмыскерлер арасындағы жоғары квалификациясы бар жұмыскерлер х₂ (%) енгізуіне байланысты бір жұмыскер өндіретін өнім қатынасы зерттеліп отыр.

Кәсіпорынның нөмірі	y
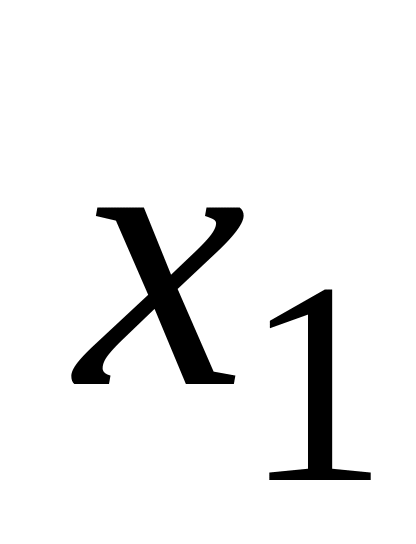
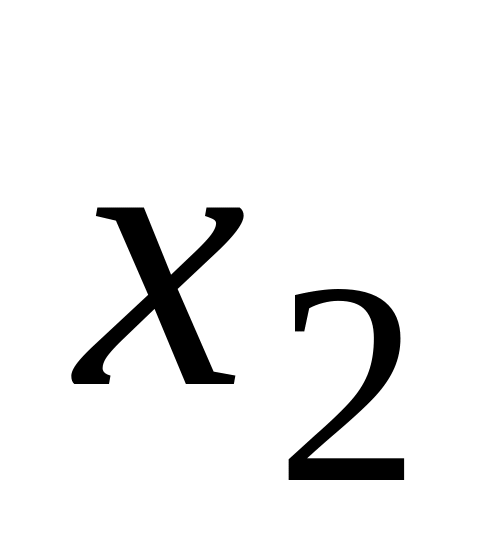
1	7,0	3,9	10,0
2	7,0	4,8	19,0
3	8,0	5,4	19,0
4	8,0	4,4	20,0
5	10,0	6,8	20,0
6	9,0	6,0	21,0
7	11,0	6,4	22,0
8	12,0	8,2	29,0
9	14,0	9,6	32,0
10	14,0	9,0	36,0

Табу керек:

1. Жиынтық регрессияның сызықтық теңдеуін.

2. Жиынтық корреляцияның коэффициентін. Қорытынды жасаңыз.

7 Тақырып. Мультиколлинеарлық.

Мысал. 20 жұмысқер бойынша толем ақы у (ақша бірліктері), жас шамасы х₁ (жылдар), мамандықты жұмыс істеген жылдар мерзімі х₂(жыл), өнім өндіру х₃ (жұмысшыға дана есебінде бір ауысым ішіндегі) деректері бар.

Бақылаудың нөмірі	- жалақы	- жас шамасы	-мамандық бойынша жұмыс мерзімі	х3 - өнім өндіру
1	300	29	6	17
2	400	40	19	25
3	300	36	10	15
4	320	32	10	17
5	200	23	3	15
6	350	45	20	18
7	350	38	17	17
8	400	40	23	25
9	380	50	31	19
10	400	47	25	23
11	250	28	7	15
12	350	30	7	18
13	200	25	6	16
14	400	48	20	23
15	220	30	5	18
16	320	40	15	18
17	390	40	20	25
18	360	38	20	26
19	260	29	10	18
20	250	25	5	17

Жалақы бойынша жиынтық регрессиялық моделі жасалған: .

Факторлар арасындағы мультиколлинеарлықтын бар болуын тексеріп және, егер мультиколлинеарлық бар болса, оны жою керек.

Шешуі. Ең алдымен қосақты корреляция коэффициенттерін табамыз. Соңғы жолда сәйкес бағана бойынша соммасының көрсеткіші болатындай етіп, кесте құрамыз:

	300	29	6	17	400	44,22	63,20	4,41
	400	40	19	25	6400	18,92	25,50	34,81
	300	36	10	15	400	0,12	15,60	16,81
	320	32	10	17	0	13,32	15,60	4,41
	200	23	3	15	14400	160,02	119,90	16,81
	350	45	20	18	900	87,42	36,60	1,21
	350	38	17	17	900	5,52	9,30	4,41
	400	40	23	25	6400	18,92	81,90	34,81
	380	50	31	19	3600	205,92	290,70	0,01
	400	47	25	23	6400	128,82	122,10	15,21
	250	28	7	15	4900	58,52	48,30	16,81
	350	30	7	18	900	31,92	48,30	1,21
	200	25	6	16	14400	113,42	63,20	9,61
	400	48	20	23	6400	152,52	36,60	15,21
	220	30	5	18	10000	31,92	80,10	1,21
	320	40	15	18	0	18,92	1,10	1,21
	390	40	20	25	4900	18,92	36,60	34,81
	360	38	20	23	1600	5,52	36,60	15,21
	260	29	10	18	3600	44,22	15,60	1,21
	250	25	5	17	4900	113,42	80,10	4,41
	6400	713	279	382	91400	1272,55	1226,95	233,8

, ,

,

Енді орташа квадраттық ауытқуларды табамыз:

, ,

,

Кейін айнымалылар көбейтіндісіне орташа мәндерін табамыз:

№
1	8700	1800	5100	174	493	102
2	16000	7600	10000	760	1000	475
3	10800	3000	4500	360	540	150
4	10240	3200	5440	320	544	170
5	4600	600	3000	69	345	45
6	15750	7000	6300	900	810	360
7	13300	5950	5950	646	646	289
8	16000	9200	10000	920	1000	575
9	19000	11780	7220	1550	950	589
10	18800	10000	9200	1175	1081	575
11	7000	1750	3750	196	420	105
12	10500	2450	6300	210	540	126
13	5000	1200	3200	150	400	96
14	19200	8000	9200	960	1104	460
15	6600	1100	3960	150	540	90
16	12800	4800	5760	600	720	270
17	15600	7800	9750	800	1000	500
18	13680	7200	8280	760	874	460
19	7540	2600	4680	290	522	180
20	6250	1250	4250	125	425	85
Σ	237360	98280	125840	11115	13954	5702

Онда

, , , ,

,

Енді корреляцияның қосақты коэффициенттерін табуға болады:

, ,

,

,

,

.

Корреляциялық матрицаны құрамыз:

	1	0,935263	0,615448	0,853056
	0,935263	1	0,69661	0,849877
	0,615448	0,69661	1	0,778766
	0,853056	0,849877	0,778766	1

Факторларды мультиколлинеарлыққа тексереміз. Мультиколлинеарлық тәуелділігі бар болады, егер қос корреляция коэффициенті болса.

Мұнда және факторлар үшін осы шарт орындалады.

Осылайша, және факторлары арасында сызықтық тәуелділік бар. Мультиколлинеарлықты жою үшін айнымалыларды шығару әдісін қолданамыз. Ең кіші мәніне ие фактордан құтыламыз. Ал , (0,853056>0,849877) болғандықтан факторынан құтылған жөн. Мультиколлинеарлық түсіндірмелі, себебі жұмыс істеген жылдар көлемі жұмыскердің жасына тәуелді. факторды шығарып, регрессия теңдеуін құрамыз (6-7тақырыптарды қараңыз ).

Ол теңдеу мынадай болады: .