
- •Функцияның ақиқаттық кестесі немесе элементінің г рафикалық белгіленуі
- •Функцияның ақиқаттық кестесі
- •Конъюнктор
- •Тапсырмалар
- •Сандарды жазу жүйелері
- •Сандарды р санау жүйесінен ондық санау жүйесіне ауыстыру
- •Сандарды ондық санау жүйесінен р санау жүйесіне ауыстыру
- •Санау жүйелеріндегі арифметикалық амалдар.
 №1
семинарлық жұмыс
№1
семинарлық жұмыс
Тақырыбы: Бульдік алгебра. Логикалық амалдар, формулалар және олардың түрленуі.
Жұмыстың мақсаты: Логикалық амалдармен, функциялармен және логика заңдарымен танысу, олардың сызбасын сыза білу, формулалар және оларды түрлендіру түрлерін үйрену.
Теориядан қысқаша мағлұматтар
Математикалық логиканың негізін салушы ағылшын математигі Джордж Буль (1815 – 1864). Ол жиын теориясының логикалық түсіндірмесі туралы бірінші болып ой қозғады.
Математикалық логиканың алгебрадан айырмашылығы онда амалдар сандармен емес, пікірлермен орындалады.
Пікір дегеніміз – оқиғаның ақиқат немесе жалған екендігін айтатын кез келген ұйғарым.
Пікірді белгілеу үшін логикалық айнымал қолданылады.
Тек екі тұрақты: 1- ақиқат немесе 0-жалған белгілерімен анықталатын х шамасын логикалық айнымалы деп атайды.
 мұндағы
Х
мұндағы
Х
 U
әмбебап
көпшесі.
U
әмбебап
көпшесі.
Барлық мүмкін болатын операцияларымен бірге В жиынынан құралған алгебра логика алгебрасы немесе Бульдік алгебра деп аталады.
Әрқайсысы тек қана 0 немесе 1 екі мәнді қабылдай алатын хi айнымалыларынан тәуелді 0 немесе 1 екі мәнін қабылдайтын функцияны Бульдік функция f(x1, x2, … , xn) деп атайды.
Қарапайым логикалық амалдар:
Логикалық таріске шығару
Логикалық қосу «немесе» ()
Логикалық көбейту ).
Логикалық кері (инверсия – NOT - НЕ – ЕМЕС, белгілеутүрі: ⌐, − ). Логикалық теріске шығару деп нәтижесі бастапқы пікірге «қарама-қайшы» пікірді айтады. Логикада А пікірін “екі рет терістеу” А пікірін береді.
Бұл бір айнымалының функциясы:
f(x)
=
 ;
;

Функцияның ақиқаттық кестесі
|
инвертор |
2.
Логикалық
қосу
(дизъюнкция – OR– ИЛИ – НЕМЕСЕ, белгілеу
түрлері: \/, 1 , +,
 ).
Бұл бірнеше айнымалының функциясы.
Функция келесі түрде бейнеленеді:
f(x1,x2)
= x1
V x2
V x3…
).
Бұл бірнеше айнымалының функциясы.
Функция келесі түрде бейнеленеді:
f(x1,x2)
= x1
V x2
V x3…
Функцияның ақиқаттық кестесі немесе элементінің г рафикалық белгіленуі
x1 |
x2 |
f(x1\/x2) |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
Дизъюнктор
3. Логикалық көбейту (конъюнкция – AND – И – ЖӘНЕ, (белгілеу түрлері: /\, &, *, ∩). Бұл бірнеше айнымалының функциясы. Функция келесі түрде белгіленеді: f(x1x2) = x1 /\ x2 /\ х3 …
Функцияның ақиқаттық кестесі
ЖӘНЕ элементтің графикалық белгіленуі:
-
x1
x2
f(x1/\x2)
0
0
0
0
1
0
1
0
0
1
1
1
Х1 /\
Х2

Конъюнктор
4. Шеффер функциясы – кері көбейтуді жүзеге асырады. Бұл бірнеше айнымалылар функциясы. Функция келесі түрде болады ( | - Шеффер штрихы деп аталады):
(x1x2) = x1x2 = x1 /\ x2
Функцияның ақиқаттық кестесі |
ЖӘНЕ – ЕМЕС элементінің графикалық белгіленуі |
|||||||||||||||
|
|
5. Пирс функциясы логикалық кері қосуды жүзеге асырады. Бұл бірнеше айнымалылар функциясы. Функция келесі түрде болады (↓ – Пирс бағыттауышы деп аталады):
 f(x1x2)
= x1
x2
= x1
x2
f(x1x2)
= x1
x2
= x1
x2
Функцияның ақиқаттық кестесі |
НЕМЕСЕ-ЕМЕС элементінің графикалық белгіленуі |
|||||||||||||||
|
|
mod 2 бойынша қосу. XOR логикалық операцияны орындайды. Бұл бірнеше айнымалылар функциясы және функция келесі түрде болады:
Y = x1 x2
Функцияның ақиқаттық кестесі |
XOR -элементінің графикалық белгіленуі: |
|||||||||||||||
|
х1
х2
|
2.1-кесте – Логикалық алгебраның негізгі заңдары
Заң |
НЕМЕСЕ үшін |
ЖӘНЕ үшін |
Ауыстырымдылық заңы. Коммутативтілік (латын тілінен аударғанда – ауыстыру, алмастыру) |
X1 \/ X2 = X2 \/ X1 |
X1 /\ X2 = X2 /\ X1 |
Біріктіру заңы. Ассоциативтілік (латын тілінен аударіанда – қосу, біріктіру, үйлестіру). |
X1 \/ (X2\/ X3) = (X1 \/ X2) \/ X3
|
X1 /\ (X2 /\ X3) = = (X1 /\ X2) /\ X3
|
Тарату заңы. Дистрибутивтілік (латын тілінен аударғанда – тарату, үйлестіру) |
X1 /\ (X2\/ X3) = (X1 /\ X2) \/ (X1\/ X3)
|
X1 \/ (X2 /\ X3) = = (X1 \/ X3) /\ (X1 \/ X3)
|
Де Морган ережесі
|
|
|
Жойылу заңы. Идемпотенттілік (латын тілінен аударғанды – өшу, жойылу) |
|
|
Шағылысу (жұтылу) заңы |
X1 \/ (X1 /\X2) = X1 |
X1 /\ (X1 \/ X2) = X1
|
Жабыстыру заңы
|
|
(X1\/X2)(X1\/X2) = X1
|
Айнымалы мен оның керісіне орындалатын амал. Комплементарлық заң (латын тілінен аударғанда– толықтыру)
|
х \/ х =1
|
х /\ х = 0 |
Тұрақтылар қасиеті
|
|
|
Екі рет терістеу амалы
|
|
|
Кестеде логикалық операциялардың орындалу басымдылығы көрсетілген.
2.2-кесте – Логикалық амалдардың орындалу басымдылығы
басымдылығы |
операция |
1 2 3 4 |
инверсия конъюнкция дизъюнкция mod 2 бойынша қосу |
Басымдылықтары бірдей операциялар солдан оңға қарай орындалады. Операциялардың орындалу ретін өзгерту үшін жақшаларды қолдануға болады. Жақшалардағы операциялар бірінші орындалады.
Мысал. Кез келген “n” айнымалы логикалық функциясы кесте түрінде берілуі мүмкін, ол кестенің сол жақ бөлігінде айнымалы мәндерінің барлық 2n жиынтығы, ал оң жақ бөлігінде осы жиынтықтардағы функция мәндері келтіріледі.
Мысалы: 3 айнымалы үшін мына кестедегідей болады:
2.3-кесте – 3 айнымалы үшін логикалық функция кестесі
-
x1
x2
x3
ƒ
0
0
0
0
1
1
1
1
0
1
1
1
0
1
1
1
0
1
0
1
1
0
0
1
0
1
0
0
1
1
0
1
ƒ=1 болғандағы функциядағы х жиынтығын (жолдар) бірлік жиынтық деп, ал бірлік жиынтықтар жиынын ƒ – тің бірлік жиыны деп атайды.
ƒ=0 болғандағы х жиынтығын ƒ – тің нөлдік жиынтығы деп атайды.
 Мәндер
кестесінен логикалық функцияны құрамыз.
Ол үшін функция бірге тең болған жолдағы
аргументтердің конъюнкциясын аламыз.
Егер аргумент нөлге тең болса, ол
инверсиямен алынады. Алынған конъюнкцияны
дизъюнкциямен біріктіреміз. Біздің
мысалымыз үшін үш конъюнкция берілген
(кестенің үш жолында функцияның мәні
бірге тең). Логикалық функция мына түрде
болады:
Мәндер
кестесінен логикалық функцияны құрамыз.
Ол үшін функция бірге тең болған жолдағы
аргументтердің конъюнкциясын аламыз.
Егер аргумент нөлге тең болса, ол
инверсиямен алынады. Алынған конъюнкцияны
дизъюнкциямен біріктіреміз. Біздің
мысалымыз үшін үш конъюнкция берілген
(кестенің үш жолында функцияның мәні
бірге тең). Логикалық функция мына түрде
болады:
Y = (X1 /\ X2 /\ X3) \/ (X1 /\ X2 /\ X3) \/ (X1 /\ X2 /\ X3) \/ (X1 /\ X2 /\ X3)
Аргументтің үстіндегі сызығымен инверсия белгіленеді. Бірінші конъюнкцияда Х1, Х2 аргументтері инверсиямен алынған, себебі олардың мәні кестенің екінші жолында нөлге тең. Екінші конъюнкцияда Х2,Х3 аргументтері инверсиямен алынған, себебі олардың мәні кестенің бесінші жолында нөлге тең. Үшінші конъюнкцияда Х1 мен Х3 аргументі инверсиямен алынған, себебі олардың мәні кестенің алтыншы жолында нөлге тең. Алынған конъюнкциялар дизъюнкция операцияларымен біріккен.
Логикалық функция ықшамдау үшін логикалық алгебраның негізгі заңдары қолданылады.

Осылайша мынадай түрдегі ықшамдалған өрнекті аламыз:

Осы өрнекті кестедегі мәндерді қоя отырып, тексереміз:
Х1=0; Х2=1; Х3=1; Y=1*1+0*1+0*1=1+0+0=1
Х1=1; Х2=0; Х3=1; Y=0*1+1*1+1*0=0+1+0=1
Х1=1; Х2=1; Х3=0; Y=1*0+1*0+1*1=0+0+1=1
Х1=1; Х2=1; Х3=1; Y=1*1+1*1+1*1=1+1+1=1 DоСЫЛАЙША оОО
Жұмыстың мазмұны
Нұсқа тапсырмасын алып және ақиқаттық кестесінен логикалық функцияны құру.
Логикалық функцияны өте жеңіл түрге түрлендіру.
Х1, Х2, Х3 аргументтері үшін бір және нөлді қою арқылы алынған логикалық функцияны тексеру.
Есеп берудің мазмұны:
Есептің қойылуы.
Теориядан қысқаша мәліметтер.
Логикалық операцияны түрлендірудің алгоритмі.
Төмендетілген логикалық функцияны тексеру нәтижесі.
Тапсырманы орындау.
Бақылау сұрақтарына жауап беру.
Есеп беруді дайындау және оны қорғау.
Бақылау сұрақтары:
Бульдік функцияға анықтама беріңіз.
Логикалық алгебраның негізгі функцияларын атаңыз.
Пирс функциясы үшін ақиқаттық кестесін құру.
Бульдік функция қандай мәндерге ие бола алады?
Шеффер функциясы үшін ақиқаттық кестесін құру.
Пирс функциясы қандай түрге ие?
XOR логикалық операциясы үшін ақиқаттық кестесін құрыңыз.
Х1=0, Х2=1 болғанда Y=Х1*Х2Х1*Х2 функциясының мәнін табыңыз?
Логикалық алгебраның негізгі заңдарын атаңыз.
Жоғары артықшылығы (приоритет) бар қандай логикалық операция?
Екі аргумент үшін (переместительный) орынауыстыру заңын жазыңыз.

X1=1, X2=1 болғанда Y=X1*X2X1*X2 функцияның мәнін табыңыз?
Х1=1, Х2=1 болғанда Y=X1*X2X1*X2 функцияның мәнін табыңыз?
Екі аргумент үшін (сочетательный) үлестіру заңын жазыңыз.
Әдебиеттер
Сергеев Н.П., Вашкевич Н.П. Основы вычислительной техники. Учеб. пособие для вузов. М.: Высш. шк., 1988.-311с.
Новиков Ф. А. Дискретная математика для программистов: Учебник.СПб: Питер 2002. - 304с.
Яворский В.В., Кан О.А. Дискретная математика для информационных систем. Учебник. Министерство образования и науки РК. КарГТУ, 2007.-197с.

 х
х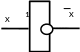 Графикалық
белгіленуі:
Графикалық
белгіленуі: f
(x1
/\
x2)
f
(x1
/\
x2)
 f(x1
x2)
f(x1
x2)


 =1
=1






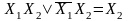

 (X1\/X2)(X1\/X2)
= X1
(X1\/X2)(X1\/X2)
= X1


