Численное интегрирование Лекция 18

 Лекция № 18 

ТЕМА: «ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ»

В рамках данн темы изучаются методы приближённого вычисления определённых интегралов, опирающиеся на суммирование с теми или иными коэффициентами значений подынтегральной функции, как правило, заданной в виде таблицы.

Обычный и естественный приём численного интегрирования состоит в замене на отрезке интегрирования подынтегральной функции интерполирующей её функцией сравнительно простого вида (например, полиномом) с последующим аналитическим интегрированием полученного подынтегрального выражения. При этом важным шагом организации численного процесса становится оценка погрешности численного интегрирования, обусловленной заменой функции интерполирующим полиномом.

В конспекте особое внимание уделяется построению эффективных алгоритмов, обеспечивающих с минимальными вычислительными затратами, вычисление интегралов с наперёд заданной точностью.

1. Постановка задачи численного интегрирования.

Как известно из математического анализа, если функция f(x) непрерывна на отрезке [a, b] и известна её первообразная F(x), т.е. F’ (x) = f(x), то определённый интеграл от функции f(x) в пределах от a до b может быть вычислен по основной формуле интегрального исчисления [1, стр. 340]:

Однако во многих случаях первообразная функция F(x) не может быть найдена с помощью элементарных средств или является слишком сложной; вследствие этого вычисление определённого интеграла по формуле Ньютона – Лейбница (1) может быть затруднительным или даже практически невыполнимым.

Кроме того, на практике подынтегральная функция f (x) часто задаётся таблично и тогда само понятие первообразной, в контексте применения формулы (1), теряет смысл. Поэтому на практике важное значение имеют приближённые и в первую очередь численные методы вычисления определённых интегралов.

Задача приближённого или численного интегрирования функций заключается в вычислении значения определённого интеграла на основе ряда значений его подынтегральной функции.

Численное вычисление однократного определённого интеграла называется механической квадратурой, а соответствующие формулы - квадратурными.

Численное вычисление двойных интегралов называется механической кубатурой, а соответствующие формулы - кубатурными.

2. Квадратурные формулы прямоугольников.

Определение определённого интеграла Римана.

Пусть на отрезке [a, b] задана некоторая непрерывная функция y = f(x) (или функция y = f (x), имеющая на отрезке [a, b] конечное число точек разрыва первого рода), тогда для неё существует число I, называемое интегралом Римана:

которое может быть вычислено по определению, как [1, стр. 32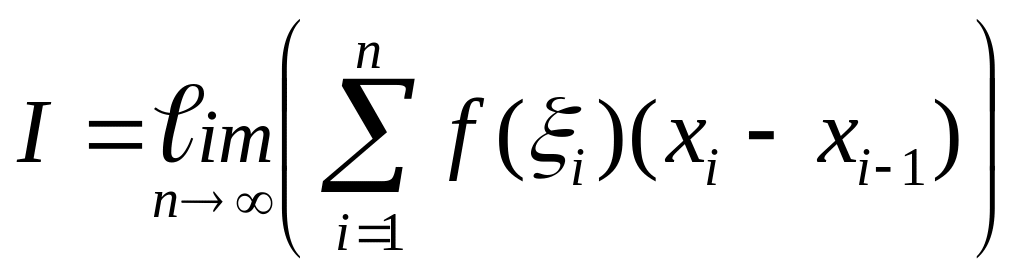3]:

(3)

при условии, что:

 произвольная упорядоченная система точек отрезка [a, b] такая, что max{x0 - a…, xi - xi1,…,b - xn} ® 0, при n ®¥, а xi – произвольная точка элементарного промежутка [x i1, xi].

(4)

Таким образом, в математическом анализе определённый интеграл Римана определяется как число, равное пределу «сумм Римана» (3), вычисляемому при выполнении условий (4).

Отметим, что в математическом анализе существует соответствующая теорема, утверждающая, что если функция y = f(x) непрерывна на отрезке [a, b] или имеет на [a, b] конечное число точек разрыва первого рода, то она интегрируема на [a, b] по Риману, т.е. предел I (3) существует и единственен.

Поэтому (например, в случае, когда f(x) ³0) интуитивно понятный способ приближённого вычисления определённого интеграла (2) как раз и базируется на определении (3) – (4), в котором (с точки зрения графического изображения) значение интеграла I определяется как площадь «криволинейной трапеции» с основанием [a, b] и «крышей» f(x) (рис. 1).

Рисунок 1 – Графическая иллюстрация общей формулы прямоугольников (5)

Для вывода квадратурной формулы прямоугольников зафиксируем величину n ³ 1 в определении интеграла (3), тогда из формулы (3) очевидно, что

(5)

Приближённое равенство (5) называется общей формулой прямоугольников, при этом «истинное значение» определённого интеграла, соответствующее площади криволинейной трапеции, приближённо заменяется площадью ступенчатой фигуры, составленной из прямоугольников, основаниями которых служат отрезки [x _i1, x_i], а высотами – ординаты f(x_i) (рис. 1).

Чтобы из общей формулы (5) получить конструктивное правило приближённого вычисления интеграла, воспользуемся предоставляемой определением (3) – (4) свободой расположения точек x_i, разбивающих промежуток интегрирования [a, b] на элементарные отрезки [x_i1, x_i], и свободой выбора точек x_i на этих отрезках.

В этой связи примем такую систему разбиения отрезка [a, b], при которой узлы x_i являются точками разбиения отрезка [a,b] на элементарные промежутки равной длины: h = (b – a)/n. Полагая при этом, что x₀ = a, x_i = x _i1 + h, (i = 1, 2,…, n – 1), x_n = b, перепишем формулу (5) в виде:

(6)

Теперь дело за тем как зафиксировать точки x_i на элементарных отрезках [x _i1, x_i] длины h. В этой связи рассмотрим ниже три возможных случая.

1). Положим x_i = x_i1, тогда из (6) получаем:

формула левых прямоугольников (7).

2). Пусть в (6) x_i = x_i,тогда получаем:

формула правых прямоугольников (8).

Формулы (6) и (7) называются соответственно квадратурными формулами левых и правых прямоугольников.

Совершенно очевидно, что если f(x) монотонная функция, то формулы (7) – (8) дают двустороннее приближение (сверху и снизу) к значению интеграла I от монотонной функции (рис. 2 a, б). Поэтому можно рассчитывать получить большую точность при вычислении значения интеграла, если взять точку x_i посередине между точками x _i1 и x_i. Отсюда приходим к рассмотрению следующего третьего случая.

3). Зафиксируем точку x_i в центре элементарного отрезка [x_i1, x_i.], т.е. считаем, что

.

В результате получаем квадратурную формулу средних прямоугольников или формулу средней точки.

Рис. 2 a I^П оценка (сверху) значения интеграла от монотонной функции

Рис. 2 б I^П+ оценка (снизу) значения интеграла от монотонной функции

Погрешность квадратурной формулы прямоугольников.

Обычный и естественный приём численного интегрирования состоит в замене на отрезке интегрирования подынтегральной функции f(x) интерполирующей её функцией  (x) сравнительно простого вида (например, полиномом) с последующим аналитическим интегрированием. Это приводит к представлению:

где R[f] – ошибка (остаточный член) квадратурной формулы, обусловленная заменой функции f(x) интерполирующим полиномом  (x).

При пренебрежении величиной R[f] получаем приближённую формулу численного интегрирования:

При таком подходе важным шагом организации численного процесса становится оценка величины погрешности численного интегрирования R[f].

Полученные из определения интеграла Римана квадратурные формулы прямоугольников (6) – (8) не содержат в себе сведений, позволяющих определить, каким нужно выбрать число n элементарных промежутков [x_i1, x_i.] или, иначе, каким должен быть шаг h разбиения отрезка интегрирования [a, b], чтобы, используя их, можно было бы найти значение определённого интеграла I с наперёд заданной точностью e. На этот вопрос можно ответить получив выражение для оценки погрешности формулы прямоугольников.

Вывод формулы для оценки погрешности квадратурной формулы прямоугольников (оценка погрешности метода интегрирования по формуле прямоугольников).

Оценим (методическую) погрешность квадратурной формулы средней точки [2. стр. 83] в предположении, что функция f(x) является дважды непрерывно дифференцируемой на отрезке [a, b], т.е. f(x)  С²_{[a, b]}.

Зададим на отрезке [a, b] равномерную сетку, разбивающую отрезок [a, b] на n равных элементарных отрезков [x_i1, x_i], так чтобы:

x₀ = a, x_i = x₀ + ih, (i = 1, 2,…, n - 1), x_n = b; h = [b - a]/n.

Тогда пользуясь аддитивностью определённого интеграла, относящемуся к промежутку интегрирования [a, b] при указанном выше способе его разбиения, имеем:

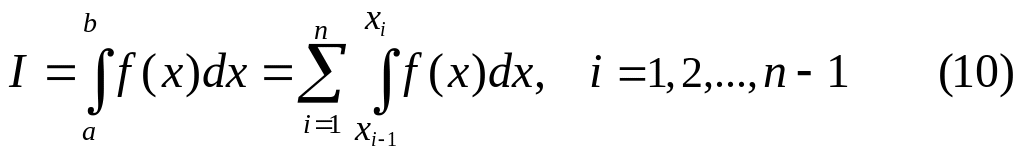
Далее среднюю точку отрезка [x_i1, x_i] будем обозначать как .

Поскольку f (x)  С²_{[a, b]}, то на каждом из отрезков [x_{i 1}, x_i] представим функцию f(x) в виде её разложения (в окрестности средней точки _i) в ряд Тейлора с остаточным членом в форме Лагранжа:

f (x) = f(_i) + ,

где _i некоторая внутренняя точка отрезка [x_i1, x_i], т.е. _i  (x_{i 1}, x_i).

Подставляя в правую часть формулы (10) вместо f(x) её разложение в ряд Тейлора, получим:

= =

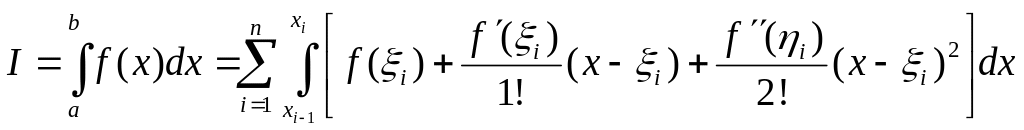(11)

Далее необходимо учесть, что при данном разбиении , а также, что

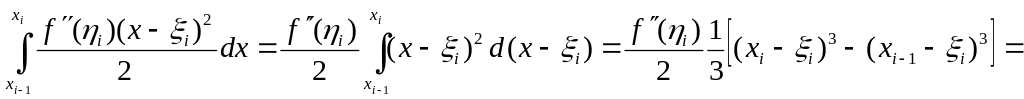
Поэтому выражение (11) можно переписать в виде:

_i  (x_{i 1}, x_i). (12)

Поскольку функция f(x) С² [a, b], то является непрерывной на [a, b], поэтому на основании обобщённой теоремы о среднем значении [3, стр. 471] на отрезке [a, b] существует такая внутренняя точка x Î (a, b), что^*:

, x Î (a, b). (13)

^* В виду того, что при изложении дальнейшего материала теорема о среднем значении [1, стр. 334] будет также востребована, то для полноты изложения её формулировка приведена в приложении к данной лекции.

С учётом представления (13), формулу (12) можно переписать в виде:

(14)

Учитывая далее, что как средняя точка отрезка [x_i1, x_i] может быть задана выражением , формулу (14) окончательно перепишем в виде:

(15)

Сравнивая формулу (15) с формулой средней точки (9), заключаем, что:

(16)

Из выражения (16) следует, что ошибка квадратурной формулы прямоугольников (средней точки) определяется выражением:

, где x Î (a, b) (17).

Поскольку интегрируемая функция f(x) является дважды непрерывно дифференцируемой на [a, b], то является непрерывной на [a, b] и, следовательно, она ограничена на [a, b], т.е. достигает на [a, b] своего максимума и минимума. Поэтому вводя в рассмотрение величину:

(18)

из формулы (17) можно получить оценку остаточной погрешности _П для формулы прямоугольников (т.е. погрешности метода интегрирования, основанного на квадратурной формуле средней точки):

_П = (19)

Из выражений (17) – (19), полученных для ошибки и остаточной погрешности формулы прямоугольников следует, что формула прямоугольников (9), (14) - (16) является точной для любой линейной функции f(x) = ax + b, поскольку вторая производная такой функции равна нулю, и, следовательно, в этом случае в нуль обращаются выражения (17) – (19).

Оценка вычислительной погрешности квадратурной формулы прямоугольников.

Пусть все значения или , фигурирующие в формулах прямоугольников (7) - (9) вычислены с одинаковой абсолютной погрешностью ^* [2. стр. 85]. То есть считаем, что в квадратурных формулах (7) - (9) вместо истинных значений используются приближённые величины , имеющие одинаковую абсолютную погрешность ^*. Тогда абсолютная погрешность _П формул (7) - (9), обусловленная суммированием в квадратурных формулах приближённых значений интегрируемой функции f(x) может быть оценена, как погрешность суммы приближённых чисел по формуле:

(20)