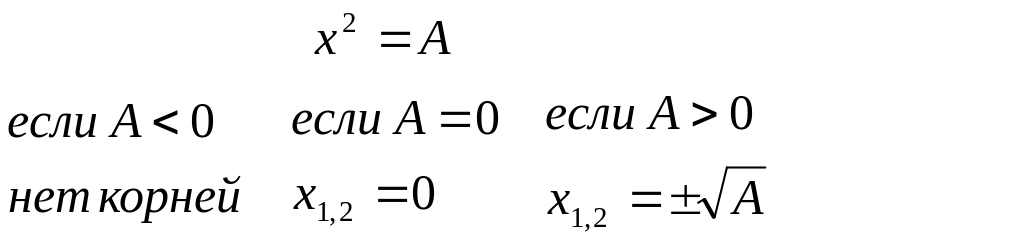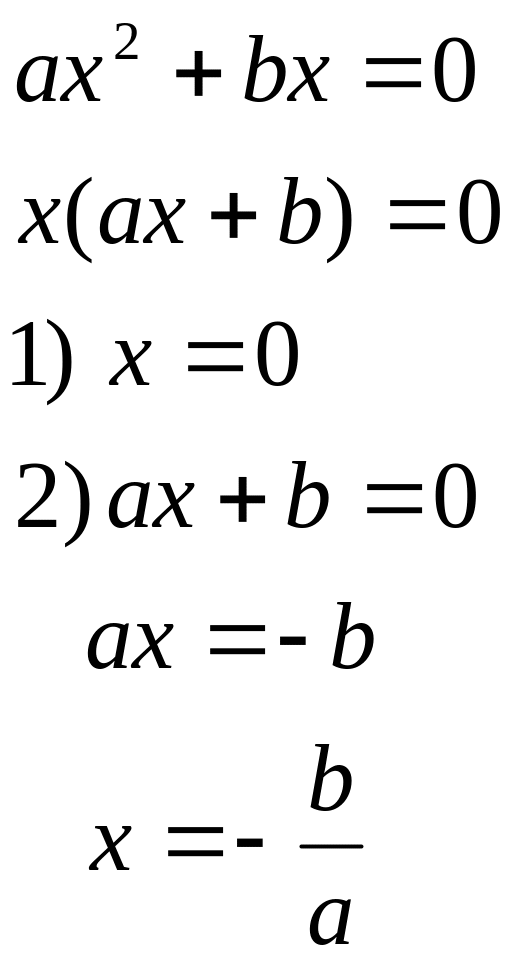Действия с дробями.

1.сложение и вычитание:

. внимание :

2.умножение дроби на число:

. числитель умножить на это число.

3.умножение дробей:

. числитель на числитель, а знаменатель на знаменатель.

4. деление дробей:

перевернуть вторую дробь, заменить деление умножением.

5. перевод десятичной дроби в простую дробь:

Для перевода надо записать десятичную дробь в виде простой по принципу «что слышу – то пишу».

Пример. 1,065 – одна целая шестьдесят пять тысячных: .

6. перевод простой дроби в десятичную дробь:

Для перевода надо поделить числитель на знаменатель в столбик.

Пример. перевести в десятичную дробь.

2 | 5 не делится, значит, дописываем ноль, ставим запятую: _20 | 5

20 0,4

0

Действия со степенями.

1.Свойства степеней ( a>0, b>0, x, y – действительные числа);

1) ; Пр1. . Пр2.

2) Пр3.

3) Пр4.

4) Пр5.

5) Пр6.

6) Пр7.

7) Пр8. . Пр9. .

8) Пр10. .

9) Пр11. .

Действия с корнями.

Опр. Арифметическим корнем n-й степени из числа a называют число b, n-ная степень которого равна a.

Пример. , т.к. ; , т.к. .

Свойства корня n-й степени ( n, k – натуральные числа, большие единицы ):

1. Корень произведения равен произведению корней.

Прим. .

2. , Корень частного равен частному корней.

3.

4. Прим. .

5. Прим.

6. Прим. .

7. Степень с рациональным показателем.

Прим1.

Прим2.

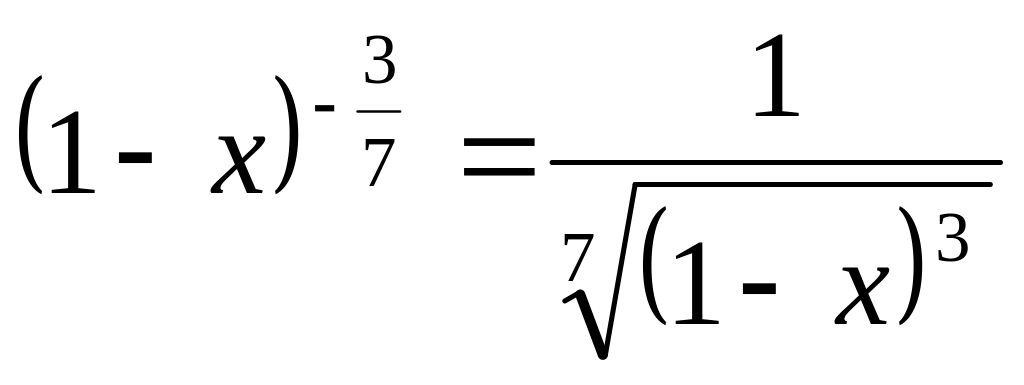
8.

Алгебраические преобразования.

Формулы сокращённого умножения:

1) - разность квадратов

Прим1.

Прим2.

2) - квадрат суммы

Прим1.

Прим2.

3) - квадрат разности

Прим.

4) - куб суммы

5) - куб разности

6) - сумма кубов

7) - разность кубов

Прим1.

Прим2.

Специальные формулы:

1) - внесение под корень

2) - вынесение общего множителя за скобки

3) - вынесение минуса

Теорема о разложении квадратного трехчлена на множители.

Квадратный трехчлен можно представить в виде: - корни соответствующего квадратного уравнения .

Прим.

Уравнения первой степени или линейные уравнения.

Такие уравнения решаются по следующему алгоритму:

1.перенести всё что с «x» – влево, всё что без «x» – вправо;

2. привести подобные слагаемые;

3. поделить обе части уравнения на коэффициент при «x».

Прим.

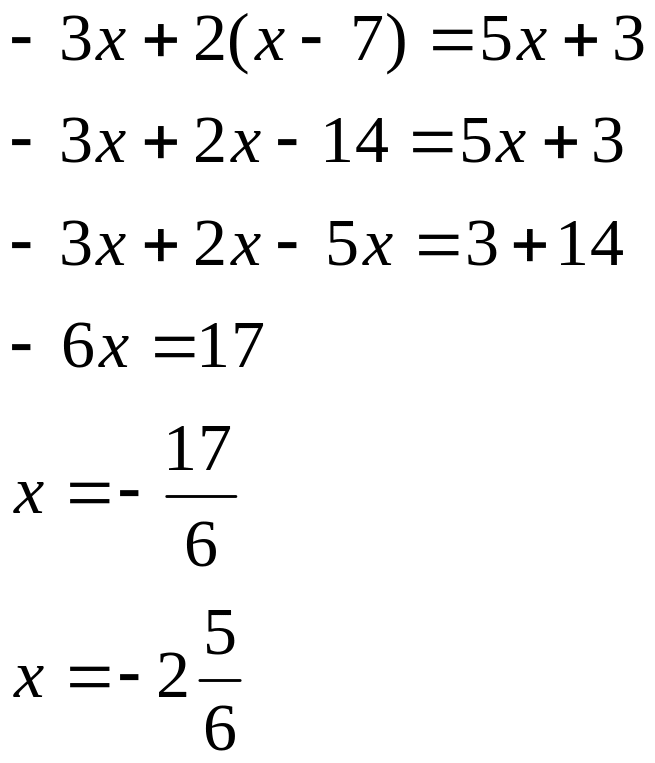
Квадратные уравнения.

Полные квадратные уравнения:

- общего вида и приведённое:

Корни ищутся по формуле: , где

Сокращённые квадратные уравнения:

, тогда: , тогда:

надо выразить x² вынести x за скобку