1.3.4 Эқк көздерін ауыстыру

ЭҚК көздерін ауыстыру негізіне есептеулерді жеңілдету үшін Кирхгофтың екінші заңы бойынша токтар қосынды контурлық ЭҚК-мен анықталады.

Кез-келген тармақтан ЭҚК көзін жою үшін осы тармаққа 1.27, в суретінде бейнеленген орнын толтыратын ( тең және оған қарама- қарсы) ЭҚК енгізеді.

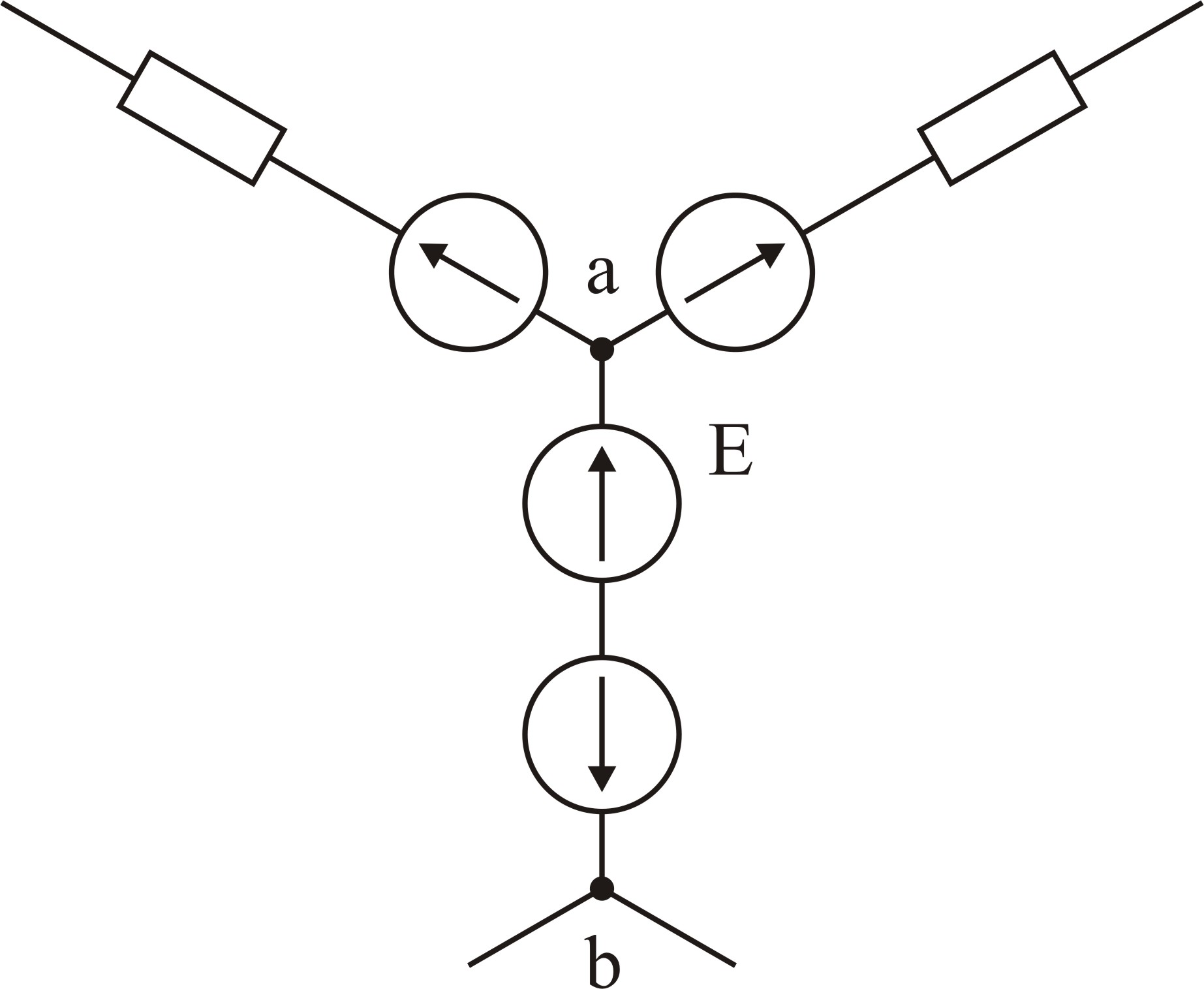
1.27 Сурет

Сондай ЭҚК осы түйінде тоғысқан тармақтарға да енгізеді. Сондықтан «ав» тармағындағы қорек көзі жойылады (1.27 сурет), ал контурлық ЭҚК өзгеріссіз қалады.

Осыдан ЭҚК көздерін ауыстыру ережесі шығады: ЭҚК көзін схеманың бір тармағынан басқа тармағына ауыстыруға болады, егер осы тармақтар бір түйінде қосылса және схемадағы токтар өзгермесе.

Кері ережесі келесідей: бір түйінде тоғысқан барлық тармақтардың ЭҚК көздерінің бағыттары мен шамалары бірдей болса, біреуін санамағанда, онда 1.28 суретінде бейнеленген барлық қорек көздері бір қорек көзімен ауыстырылады және ол қорек көзі болмаған тармаққа қосылады.

а) б)

1.28 Сурет

1.4 Контурлық токтар әдісі

1.4.1 Контурлық токтар әдісін қолдану

Контурлық токтар әдісі негізгі әдістердің біреуі болып саналады және ол тұрақты және айнымалы токтың сызықты тізбектерінде қолданылады.

Әдістің маңызы болып, ізделулі белгісіз шамалар ретінде тізбек тармақтарындағы нақты токтар қарастырылмайды, ал шартты контурлық токтар деп аталатын токтар алынады. Контурлық токтардың саны тізбектегі тәуелсіз контурлардың санына тең және тармақтардағы токтардың санынан аз болады. Сондықтан, контурлық токтар әдісін қолданған кезде Кирхгофтың екінші заңы бойынша жазылған теңдеулер жеткілікті. Контурлық токтар әдісін контурлардың саны шамалы тізбектер үшін және де ток көзі бар тізбектер үшін қолданған дұрыс.

Негізгі есептеу қатынастарын шығару үшін тармақтарында ЭҚК көздері бар тұрақты токтың тізбегін қарастырайық (1.29 сурет), онда 3 тармақ және 2 түйін бар.

1.29 Сурет

Берілген тізбек үшін тәуелсіз контурлардың саны 2 тең. I₁₁ және I₂₂ контурлық токтардың бағыттарын стрелкамен көрсетеміз. Әр контур үшін Кирхгофтың екінші заңы бойынша теңдеулер жазамыз. Көршілес тармақтағы (R₂ кедергісі) токтың (I₁₁  I₂₂) бағыты үстінен астына қарай бағытталған, яғни I₁₁ контурлық тогы бойынша бағытталған. R₁ және R₃ тармақтарында I₁₁ және I₂₂ токтары орын алады. Онда бірінші контур үшін теңдік былай көрсетіледі

R₁ I₁₁ + R₂ (I₁₁ – I₂₂) = E₁ + E₂.

екінші контур үшін

R₃ I₂₂ – R₂ (I₁₁ – I₂₂)= – E₂ – E₃.

Онда 1.29 суретіндегі схема үшін теңдеулер келесідей

(1.17)

Жаңа белгілеулерді енгіземіз

R₁ + R₂ = R₁₁ – 1 контурдың өзіндік кедергісі;

– R₂ = R₁₂ = R₂₁ – 1 және 2 контурдың жалпы кедергісі;

R₂ + R₃ = R₂₂ – 2 контурдың өзіндік кедергісі;

E₁ + E₂= E₁₁ – 1 контурдың контурлық ЭҚК;

– E₂ – E₃ = E₂₂ – 2 контурдың контурлық ЭҚК.

Онда теңдеулер жүйесі бойынша кез-келген тізбектің контурлық теңдеулерін аламыз

(1.18)

Матрица түрінде

, (1.19)

мұнда 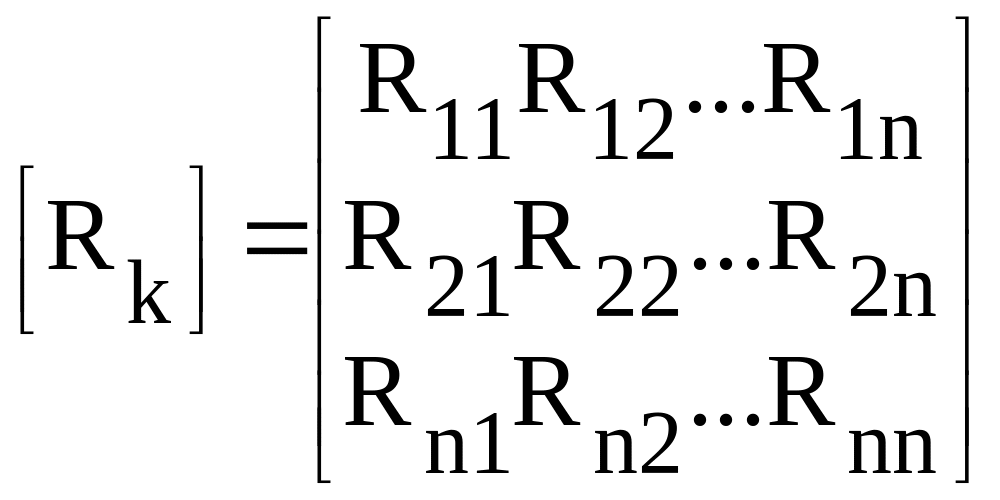– п өлшемді контурлық кедергілердің квадраттық матрицасы ;

[I_k]= – контурлық токтардың бағана матрицасы;

[E_k]= – ЭҚК бағана матрицасы.

(1.18) теңдеулерін қолмен шығаруға болады, бірақ n > 3 болған кезде есептеулер қиынға әкеледі, сондықтан оларды Крамер әдісі бойынша анықтауыштар арқылы есептеген дұрыс.

Жүйенің анықтауышы

Контурлық токтар

I₁₁= ;

I₂₂= ;

………………………

I_nn= ;

Бағана элементтері бойынша анықтауышты жіктейміз

, (1.20)

ЭЕМ қолданған кезде контурлық токтарды (1.19) формуласымен есептеген дұрыс

[I_k]=[R_K^-1]*[E_K], (1.21)

мұндағы [R_K^-1] – [R_K]* [R_K^-1]=[1] шартына сәйкес келетін контурлық кедергінің қарсы матрицасы.

Қарастырылатын тізбекте шектелген қуаттың ток көздері болса, онда баламалы ЭҚК көзімен ауыстыруға болады. Егер тізбекте шексіз қуаттың ток көздері болса, онда осы токтарды контурлық токтар ретінде алған дұрыс, өйткені контурлық токтардың сәйкесінше теңдеулердің саны азаяды.